狄克斯特拉算法
与前面提到的贝尔曼-福特算法类似,狄克斯特拉(Dijkstra)算法也是求解最短路径问题的算法,使用它可以求得从起点到终点的路径中权重总和最小的那条路径路径。
图解
01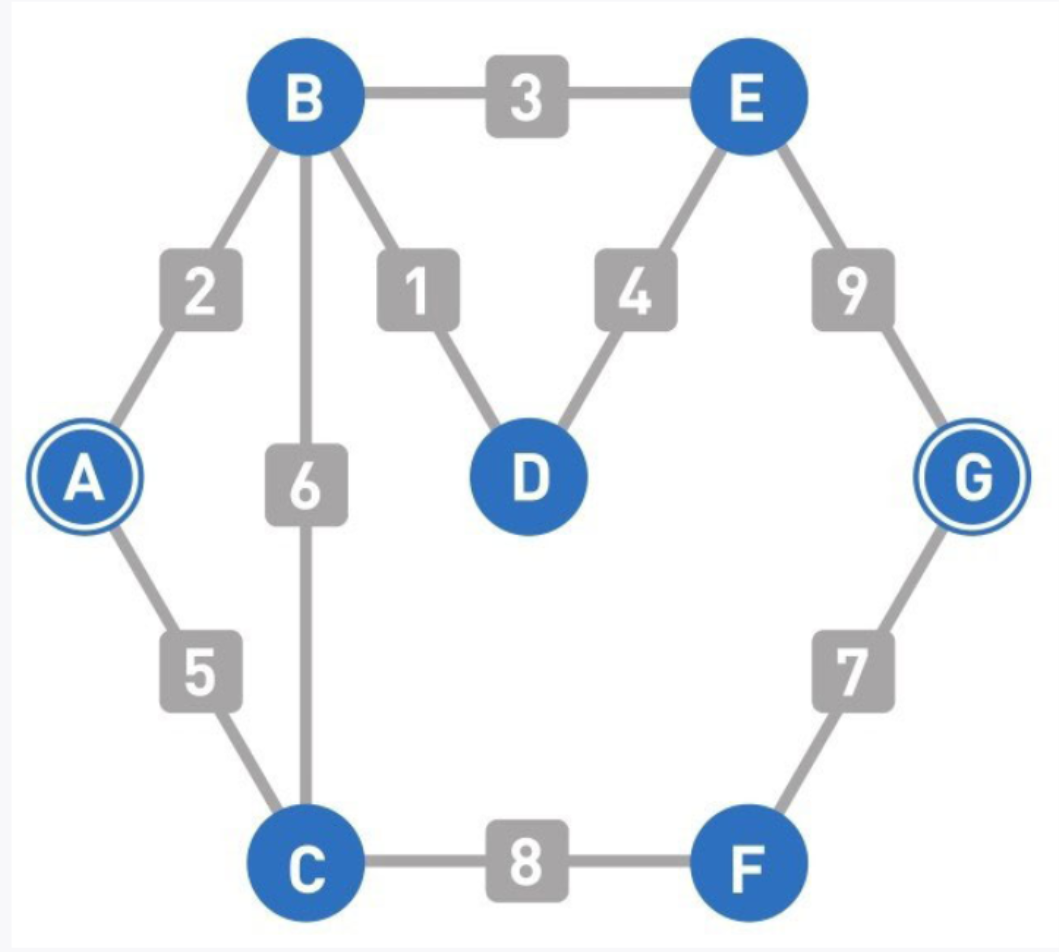
这里我们设A为起点、G为终点,来讲解狄克斯特拉算法。
02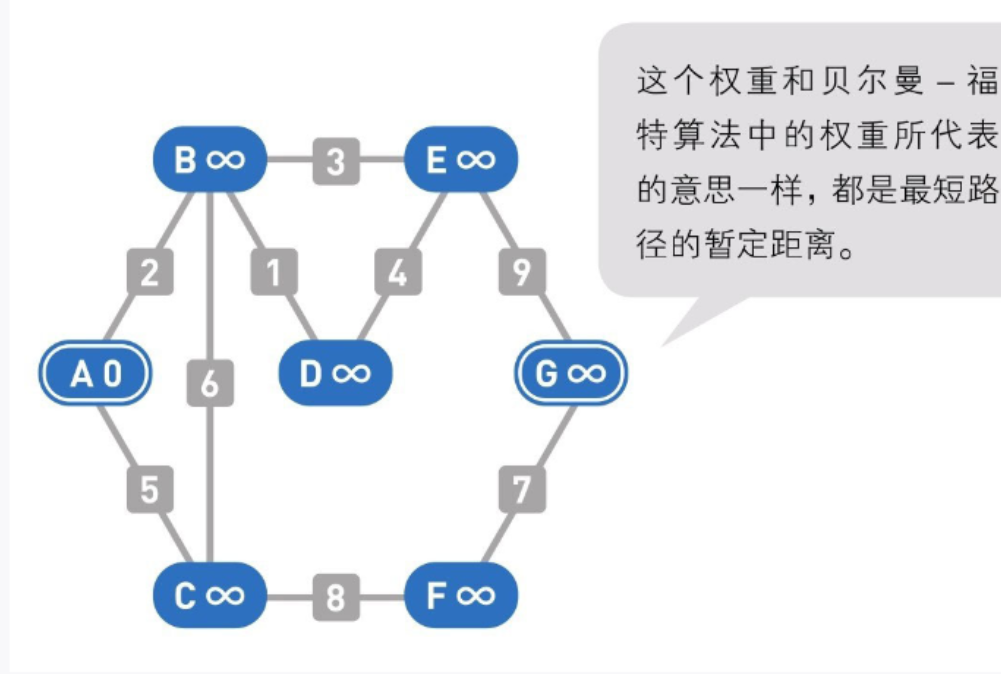
首先设置各个顶点的初始权重:起点为0,其他顶点为无穷大(∞)。
03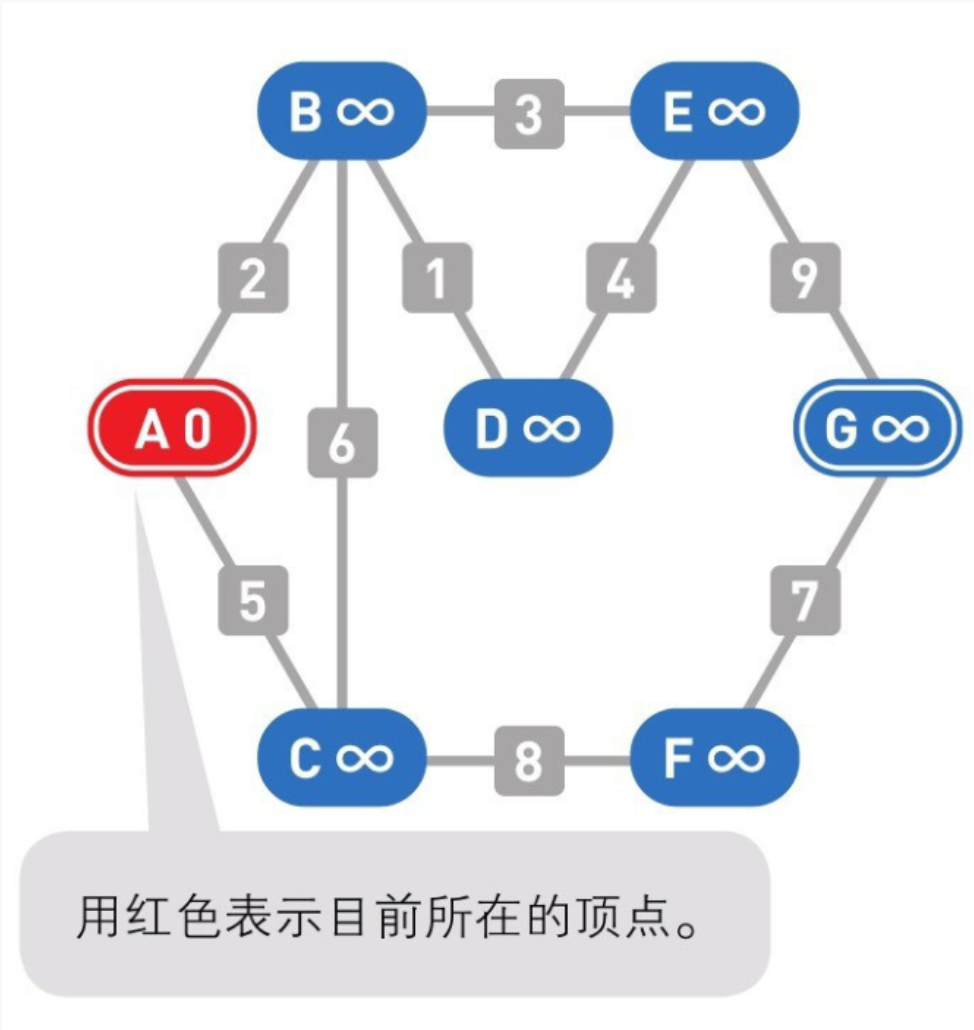
从起点出发。
04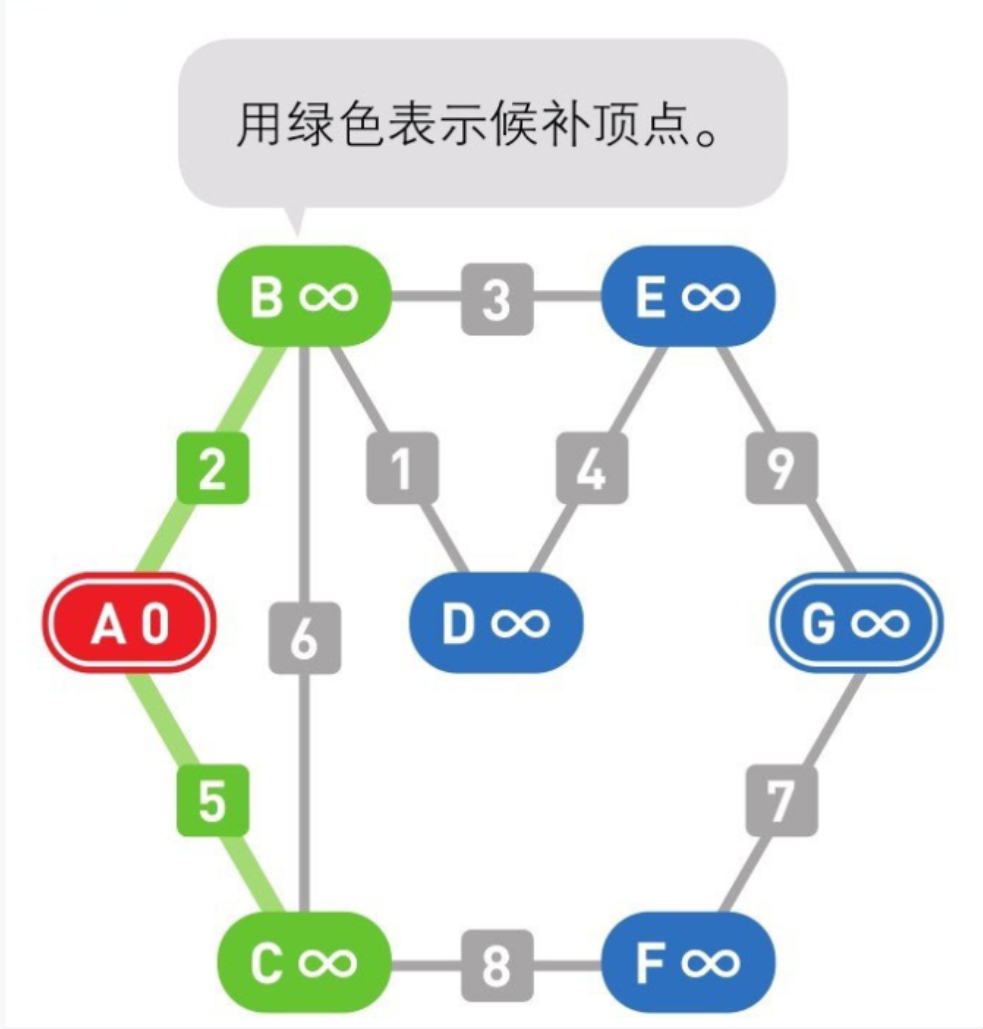
寻找可以从目前所在的顶点直达且尚未被搜索过的顶点,此处为顶点B和顶点C,将它们设为下一步的候补顶点。
05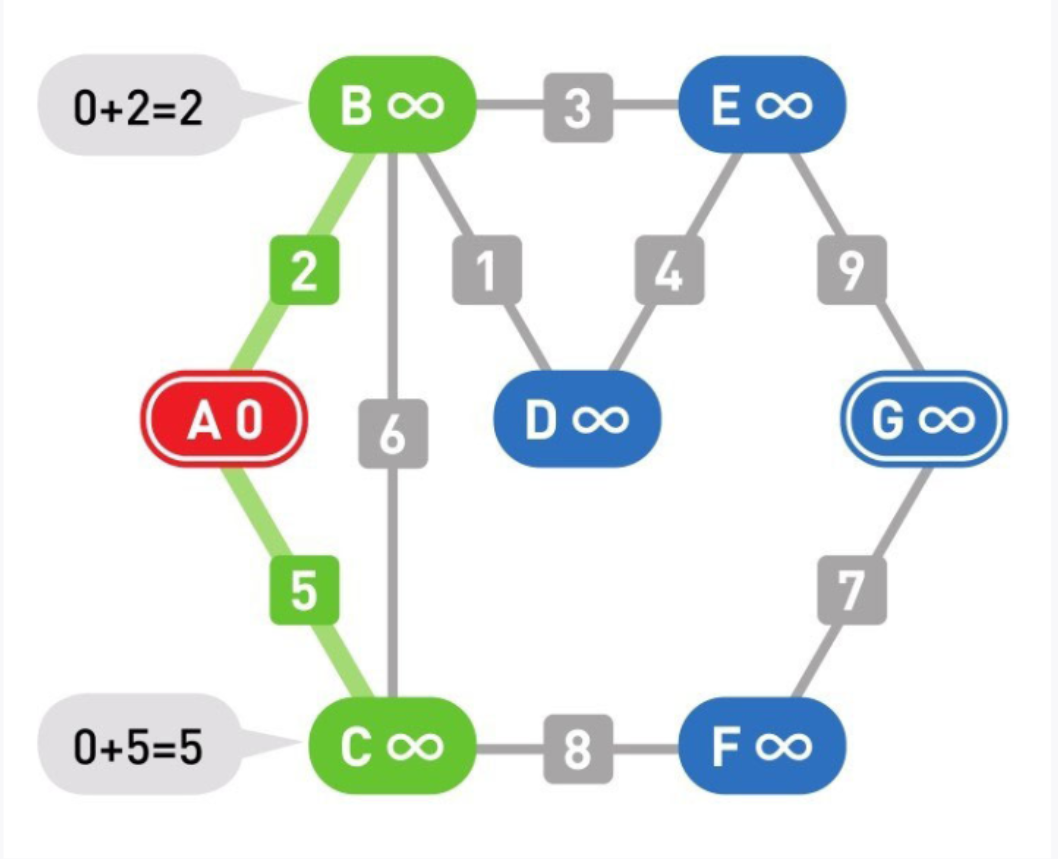
计算各个候补顶点的权重。计算方法是“目前所在顶点的权重+目前所在顶点到候补顶点的权重”。比如起点A的权重是0,那么顶点B的权重就是0+2=2。用同样的方法计算顶点C,结果就是0+5=5。
06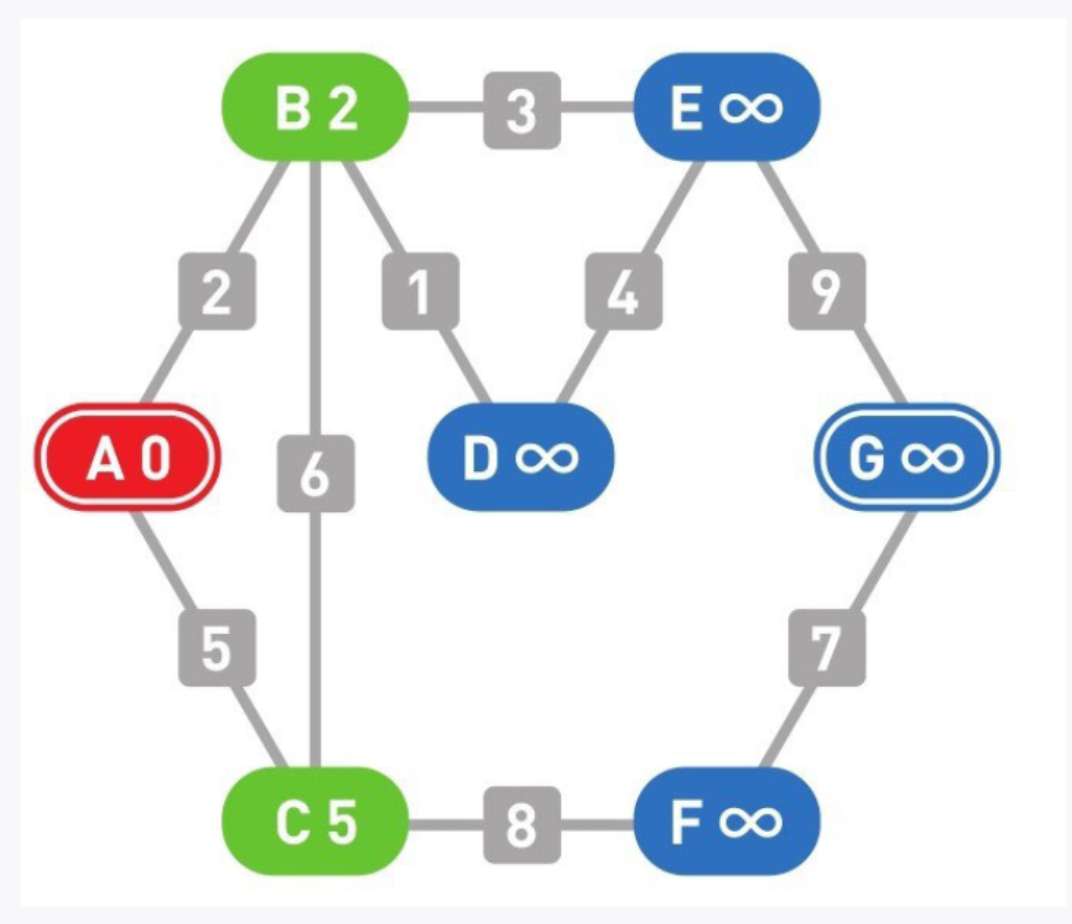
如果计算结果小于候补顶点的值,就更新这个值。顶点B和顶点C现在的权重都是无穷大,大于计算结果,所以更新这两个顶点的值。
07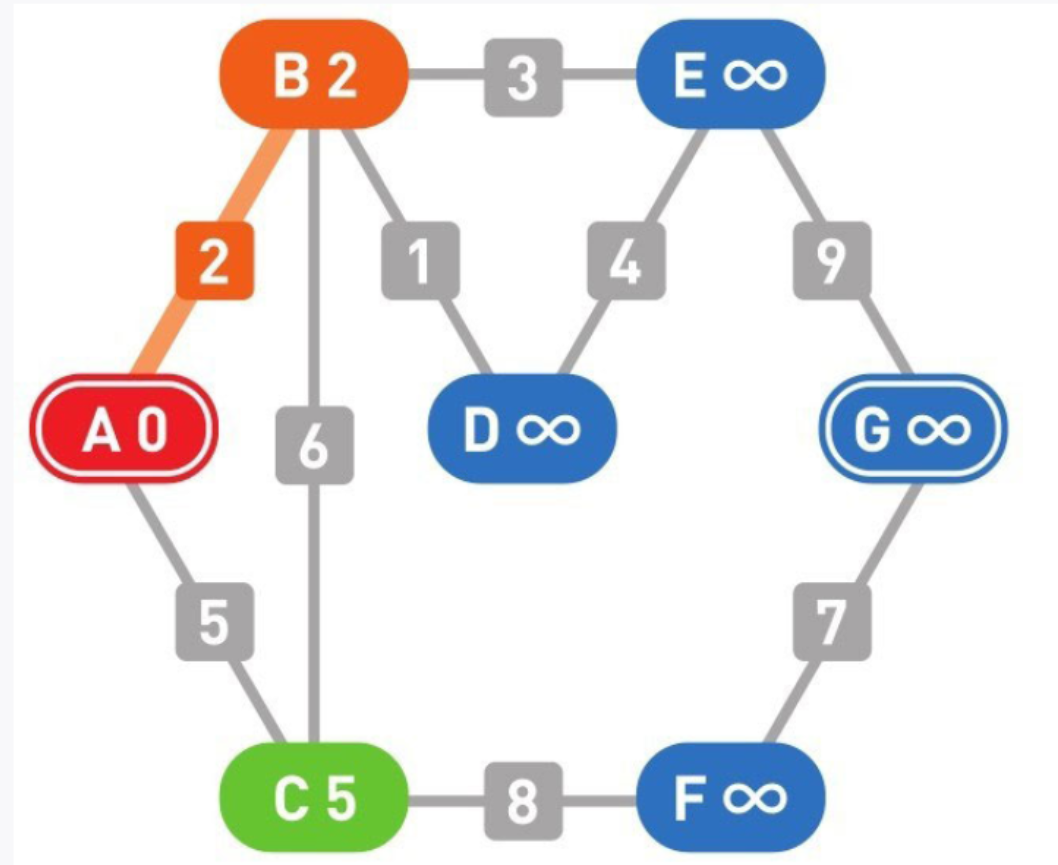
从候补顶点中选出权重最小的顶点。此处B的权重最小,那么路径A-B就是从起点A到顶点B的最短路径。因为如果要走别的路径,那么必定会经过顶点C,其权重也就必定会高于A-B这条路径。
08
确定了最短路径,移动到顶点B。
09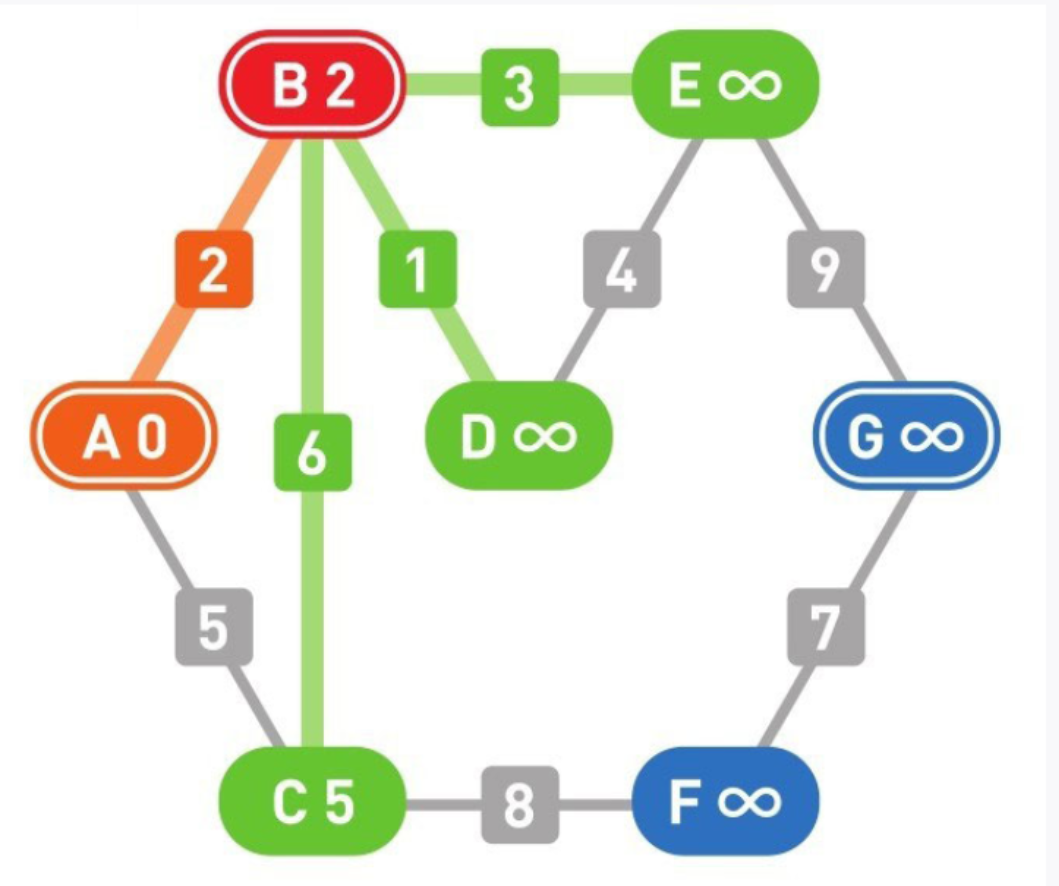
将可以从顶点B直达的顶点设为新的候补顶点,于是顶点D和顶点E也成为了候补。目前有三个候补顶点C、D、E。
10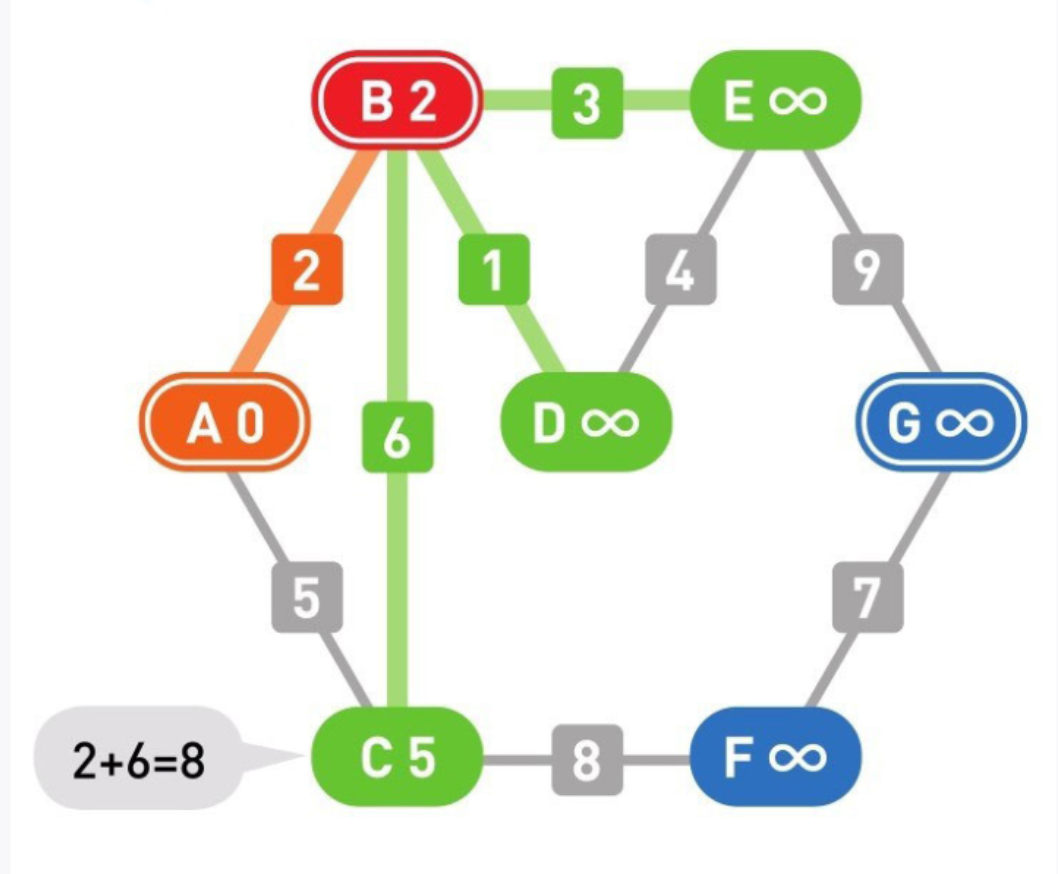
用相同的方法计算各个候补顶点的权重。从B到C的权重为2+6=8,比C当前的权重5大,因此不更新这个值。
11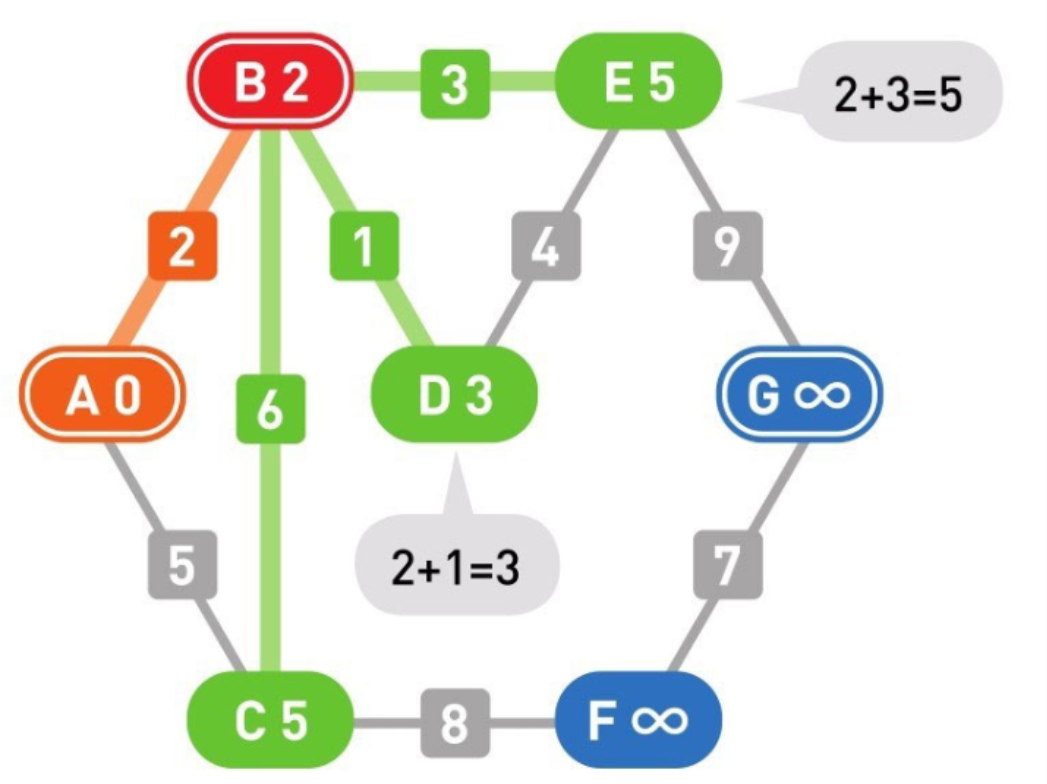
更新了剩下的顶点D和E。
12
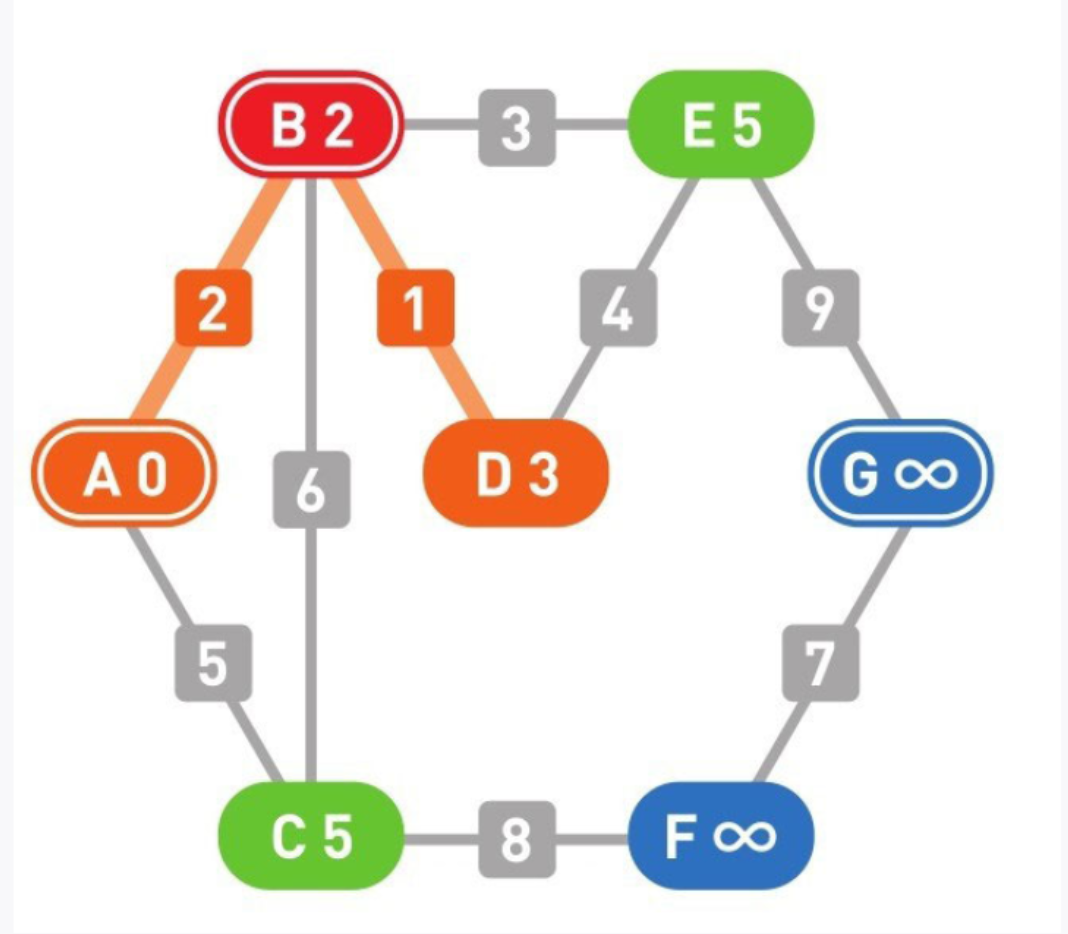
从候补顶点中选出权重最小的顶点。此处D的权重最小,那么路径A-B-D就是从起点A到顶点D的最短路径。
13
A-B-D这条路径是通过逐步从候补顶点中选择权重最小的顶点来得到的,所以如果经过其他顶点到达D,其权重必定会大于这条路径。
14
要重复执行同样的操作直到到达终点G为止。移动到顶点D后算出了E的权重,然而并不需要更新它(因为3+4=7)。现在,两个候补顶点C和E的权重都为5,所以选择哪一个都可以。
15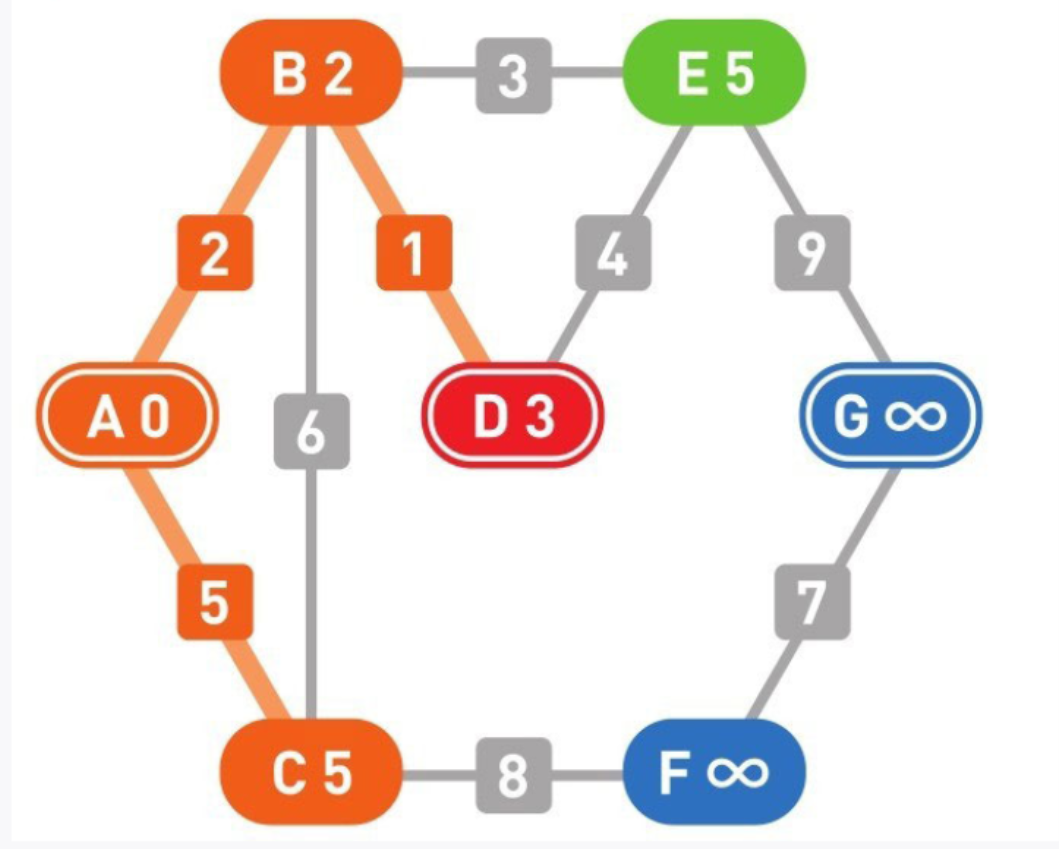
此处我们选择了C,于是起点A到顶点C的最短路径便确定了。
16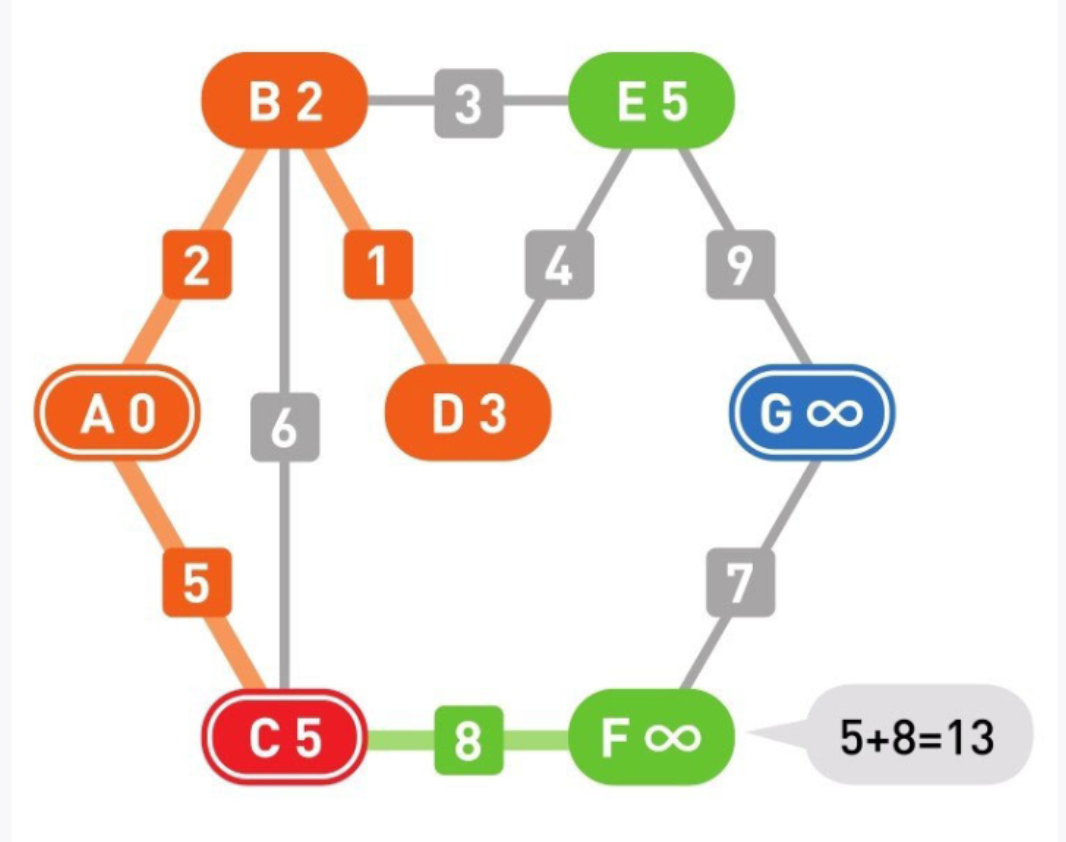
移动到C后,顶点F成为了新的候补顶点,且F的权重被更新为13。此时的候补顶点中,E为5、F为13,所以……
17
我们选择了权重更小的E,起点A到顶点E的最短路径也就确定了下来。
18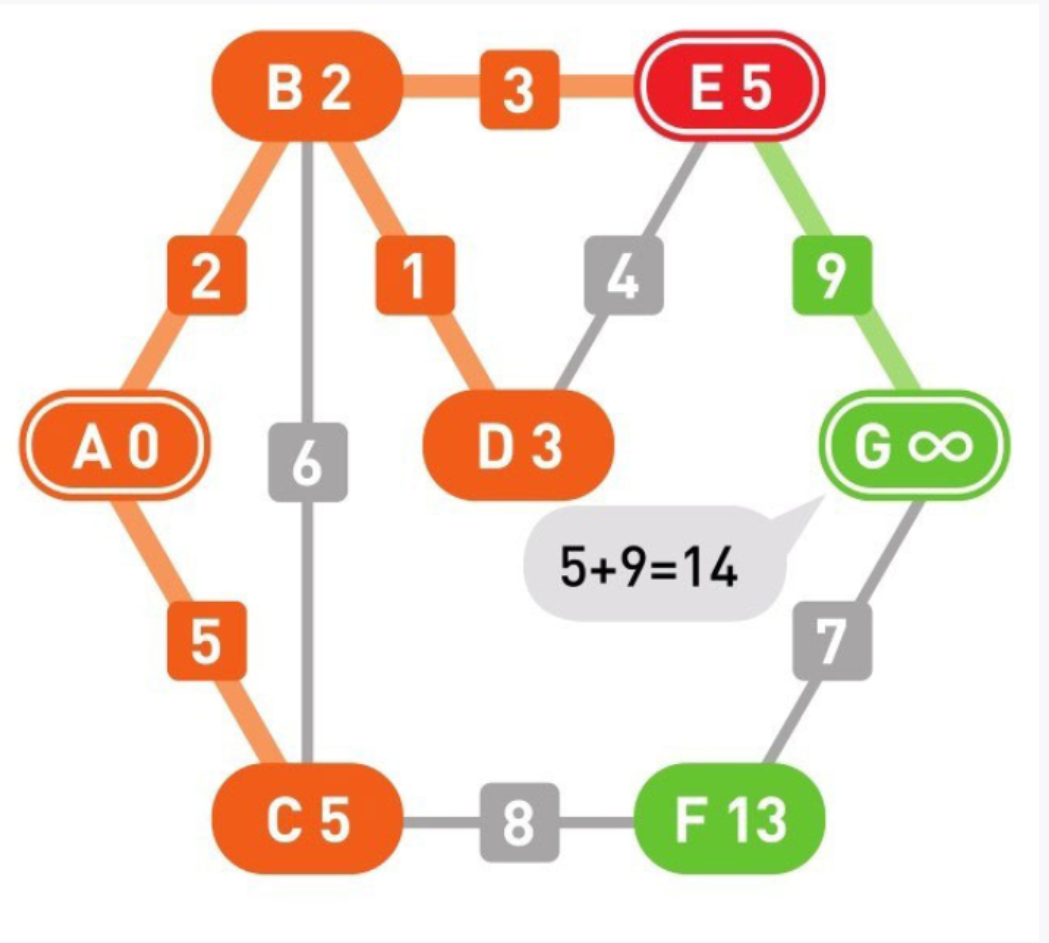
移动到E。G成了新的候补顶点,其权重也被更新为14。此时的候补顶点中,F为13、G为14,所以选择了F。由此,起点A到顶点F的最短路径也就确定了下来。
19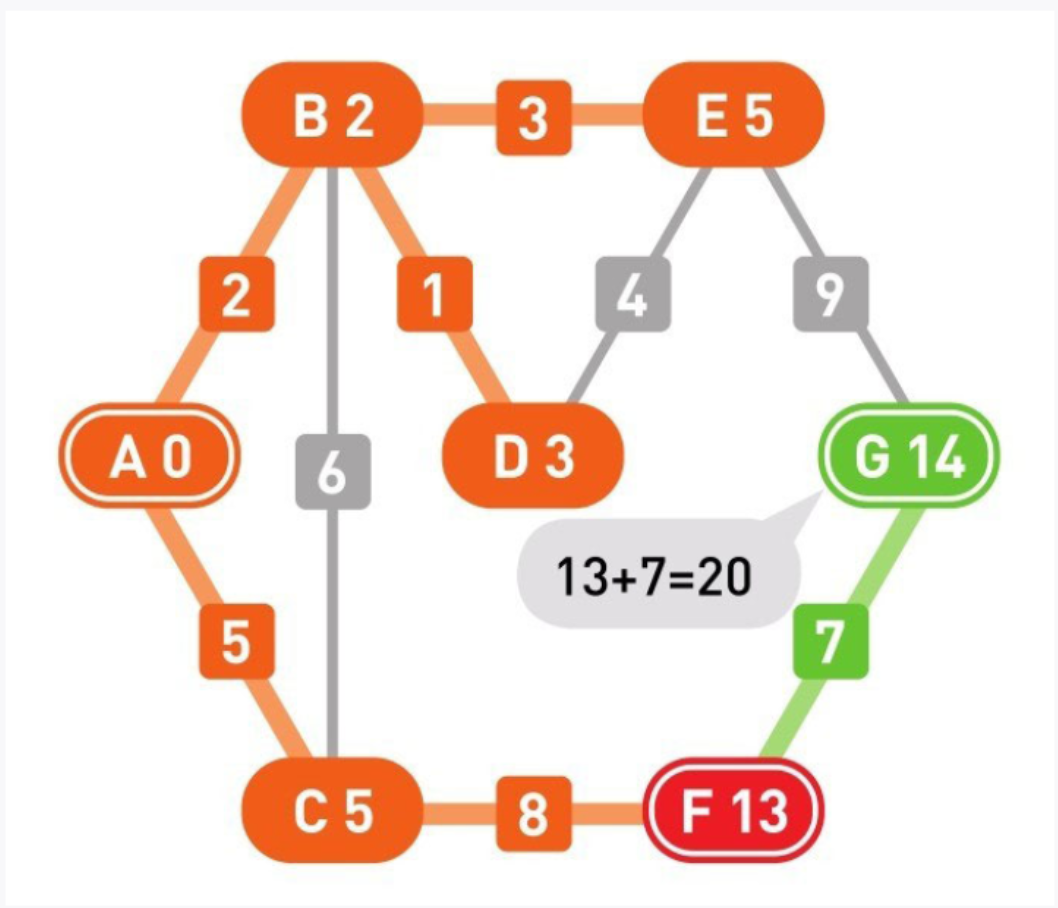
移动到F。顶点G的权重计算结果为13+7=20,比现在的值14要大,因此不更新它。由于候补顶点只剩G了,所以选择G,并确定了起点A到顶点G的最短路径。
20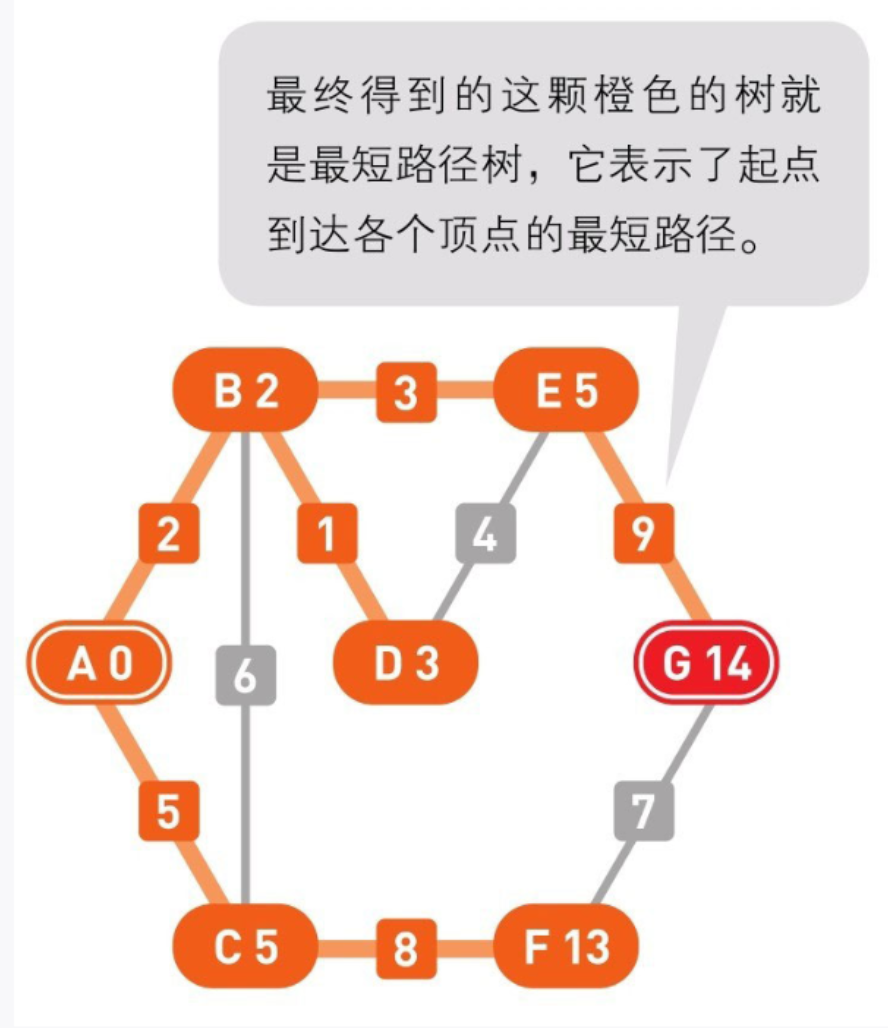
到达终点G,搜索结束。
21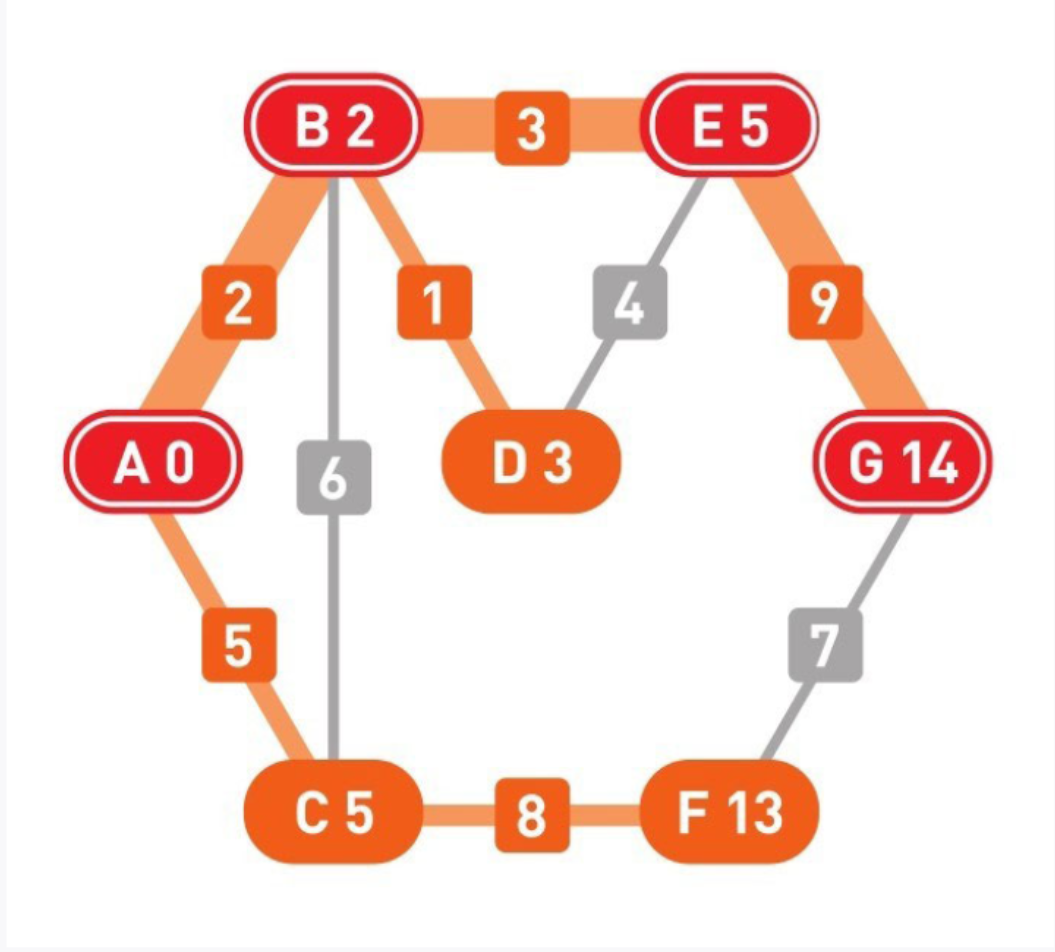
用粗线条标注的就是从起点A到终点G的最短路径。
解说
比起需要对所有的边都重复计算权重和更新权重的贝尔曼-福特算法,狄克斯特拉算法多了一步选择顶点的操作,这使得它在求最短路径上更为高效。
将图的顶点数设为n、边数设为m,那么如果事先不进行任何处理,该算法的时间复杂度就是O(n2)。不过,如果对数据结构进行优化,那么时间复杂度就会变为O(m+nlogn)。
Dijkstra算法通过不断选择当前离起始节点最近的节点,并更新与其相邻节点的距离,逐步求解从起始节点到其余各节点的最短路径。
补充说明
狄克斯特拉算法和贝尔曼-福特算法一样,也能在有向图中求解最短路径问题。
但是如果图中含有负数权重,狄克斯特拉算法可能会无法得出正确答案,这一点和贝尔曼-福特算法有所不同。比如右边这个图中,A-C-B-G为正确的最短路径,权重为4+(-3)+1=2。
然而,如果用狄克斯特拉算法来求解,得到的却是下面这样的最短路径树。从起点A到终点G的最短路径为A-B-G,权重为3。这个答案显然是错误的。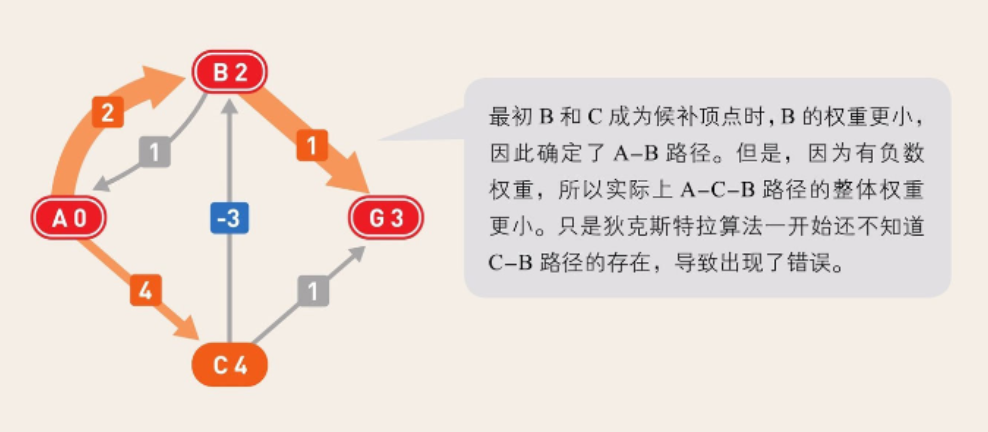
如果闭环中有负数权重,就不存在最短路径。贝尔曼-福特算法可以直接认定不存在最短路径,但在狄克斯特拉算法中,即便不存在最短路径,它也会算出一个错误的最短路径出来。因此,有负数权重时不能使用狄克斯特拉算法。
总的来说,就是不存在负数权重时,更适合使用效率较高的狄克斯特拉算法,而存在负数权重时,即便较为耗时,也应该使用可以得到正确答案的贝尔曼-福特算法。
一句话总结:
Dijkstra算法通过不断选择当前离起始节点最近的节点,并更新与其相邻节点的距离,逐步求解从起始节点到其余各节点的最短路径。
演示:
import heapq
# Dijkstra算法函数,计算起始节点到图中各节点的最短距离
def dijkstra(graph, start):
# 初始化距离字典,所有节点距离起始节点为无穷大
distances = {node: float('inf') for node in graph}
distances[start] = 0 # 起始节点到自身距离为0
pq = [(0, start)] # 优先队列,存储节点的距离和节点名称
while pq: # 当优先队列不为空时循环
current_dist, current_node = heapq.heappop(pq) # 弹出当前距禧最小的节点和距离
if current_dist > distances[current_node]:
continue # 如果当前节点已经处理过,则跳过
# 遍历当前节点的邻居节点
for neighbor, weight in graph[current_node].items():
distance = current_dist + weight # 计算邻居节点的新距离
# 如果新距离小于已知距离,则更新距离并加入优先队列
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(pq, (distance, neighbor))
return distances # 返回起始节点到各节点的最短距离字典
# 示例图
graph = {
'A': {'B': 2, 'C': 5},
'B': {'A': 2, 'C': 6, 'D': 1, 'E': 3},
'C': {'A': 5, 'B': 6, 'F': 8},
'D': {'B': 1, 'E': 4},
'E': {'D': 4, 'B': 3, 'G': 9},
'F': {'C': 8, 'G': 7},
'G': {'F': 7, 'E': 9},
}
start_node = 'A'
# 调用Dijkstra算法函数并输出结果
result = dijkstra(graph, start_node)
print(result)结果:
{'A': 0, 'B': 2, 'C': 5, 'D': 3, 'E': 5, 'F': 13, 'G': 14}
———————————————————————————————————————————
文章来源:书籍《我的第一本算法书》
书籍链接:
我的第一本算法书 (豆瓣) (douban.com)
作者:宫崎修一 石田保辉
出版社:人民邮电出版社
ISBN:9787115495242
本篇文章仅用于学习和研究目的,不会用于任何商业用途。引用书籍《我的第一本算法书》的内容旨在分享知识和启发思考,尊重原著作者宫崎修一和石田保辉的知识产权。如有侵权或者版权纠纷,请及时联系作者。
———————————————————————————————————————————