本文讨论的内容参考自《神经网络与深度学习》https://nndl.github.io/ 第3章 线性模型
线性模型
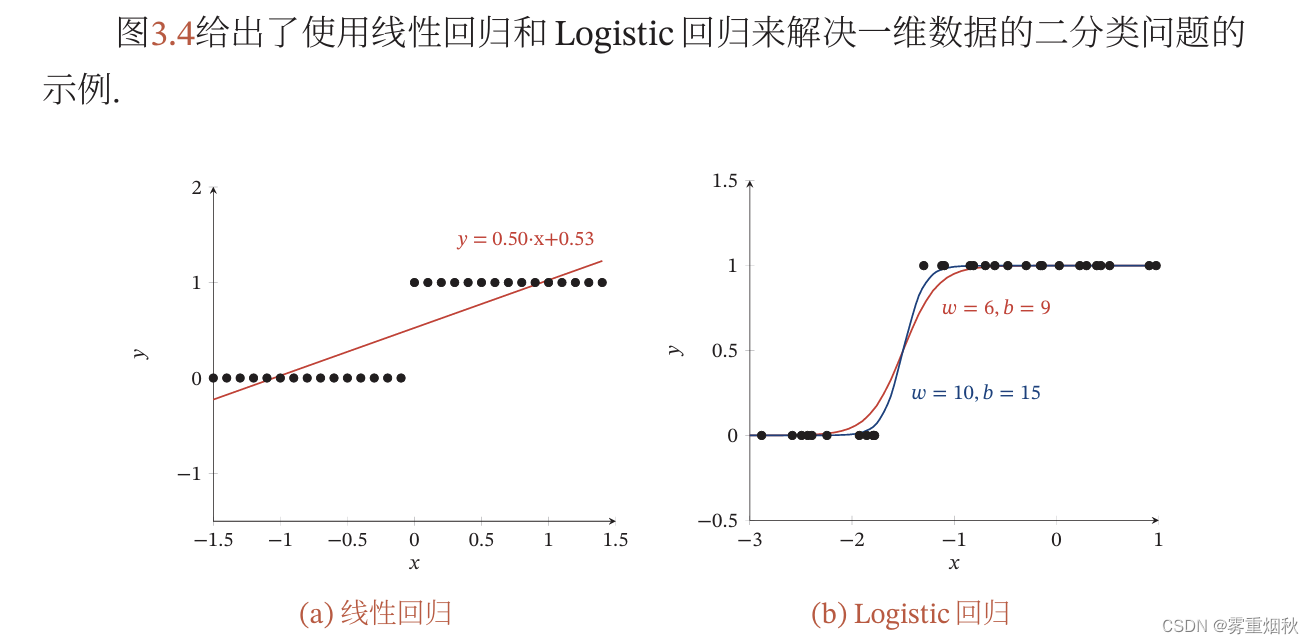
线性模型(Linear Model)是机器学习中应用最广泛的模型,指通过样本特征的线性组合来进行预测的模型,给定一个
D
D
D维样本
x
=
[
x
1
,
.
.
.
,
x
D
]
T
\bm x = [x_1,...,x_D]^T
x=[x1,...,xD]T,其线性组合函数为

在分类问题中,由于输出目标
y
y
y是一些离散的标签,而
f
(
x
;
ω
)
f(\bm x;\bm \omega)
f(x;ω)的值域为实数,因此无法直接用
f
(
x
;
ω
)
f(\bm x;\bm \omega)
f(x;ω)来进行预测,需要引入一个非线性的决策函数
g
(
⋅
)
g(\cdot)
g(⋅)来预测输出目标


线性判别函数和决策边界
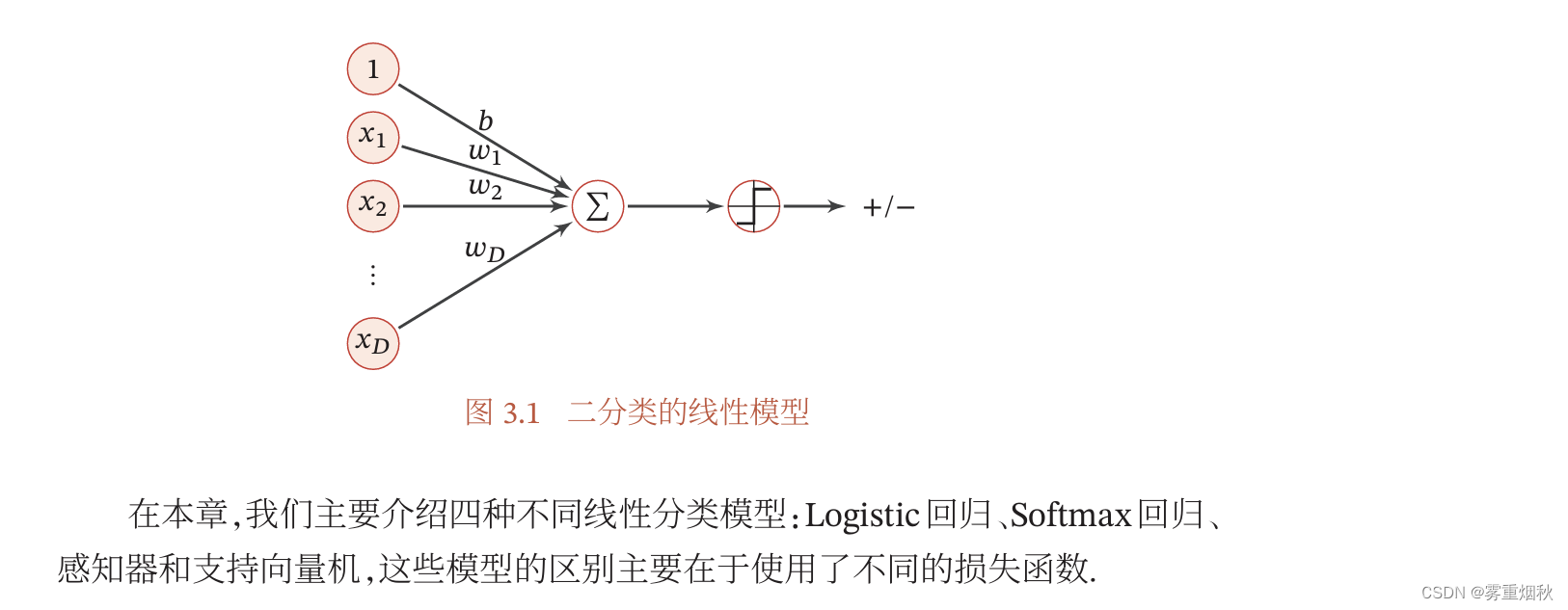
从公式(3.3)可知,一个线性分类模型或线性分类器,是由一个或多个线性的判别函数
f
(
x
;
ω
)
=
ω
T
x
+
b
f(\bm x;\bm \omega)=\bm \omega^T x+b
f(x;ω)=ωTx+b和非线性的决策函数
g
(
⋅
)
g(\cdot)
g(⋅)组成,我们首先考虑二分类的情况,然后再扩展到多分类的情况。
二分类
二分类问题的类别标签
y
y
y只有两种取值,通常可以设为
+
1
,
−
1
{+1,-1}
+1,−1或
0
,
1
{0,1}
0,1。在二分类问题中,常用正例和负例来分别表示属于类别+1和-1的样本。
在二分类问题中,我们只需要一个线性判别函数
f
(
x
;
ω
)
=
ω
T
x
+
b
f(\bm x;\bm \omega)=\bm \omega^T x+b
f(x;ω)=ωTx+b。特征空间
R
D
R^D
RD中所有满足
f
(
x
;
ω
)
=
0
f(\bm x; \bm \omega)=0
f(x;ω)=0的点组成一个分割超平面,称为决策边界或决策平面。决策边界将特征空间一分为二,划分成两个区域,每个区域对应一个类别。
所谓“线性分类模型”就是指其决策边界是线性超平面。在特征空间中,决策平面与权重向量
ω
\bm \omega
ω正交,特征空间中每个样本点到决策平面的有向距离为
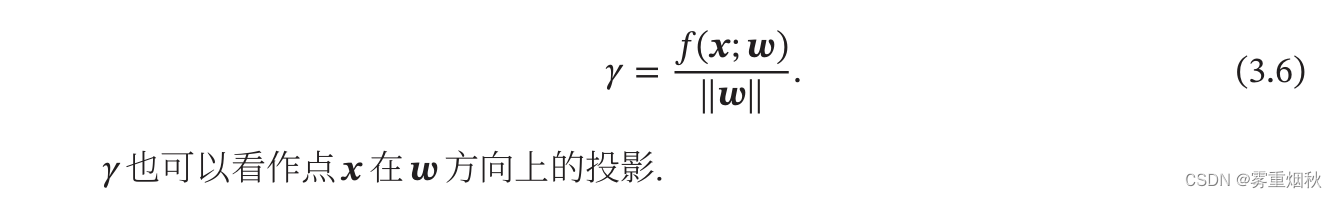
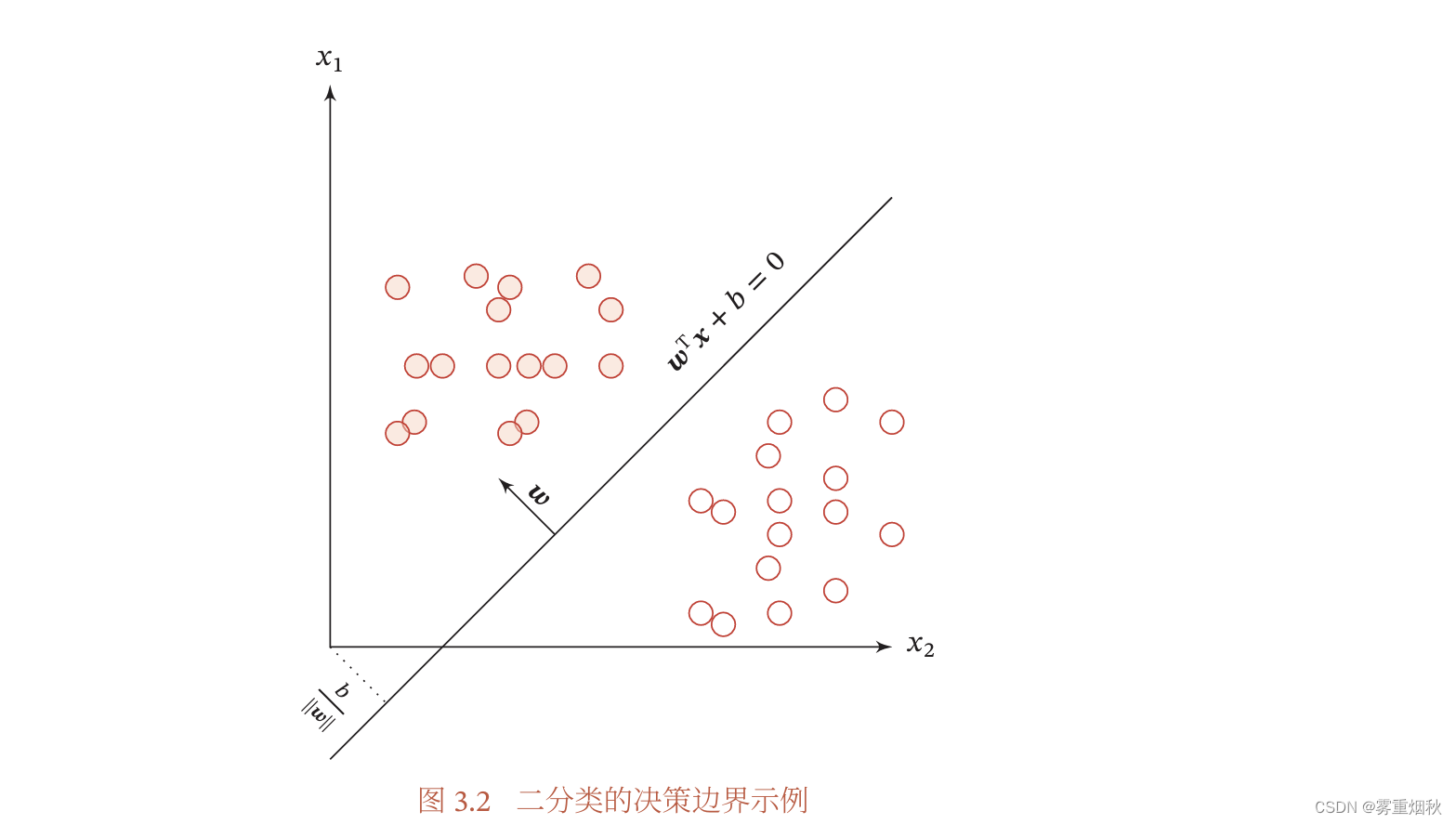
图3.2给出了一个二分类问题的线性决策边界示例,其中样本特征向量
x
=
[
x
1
,
x
2
]
\bm x=[x1,x2]
x=[x1,x2],权重向量
ω
=
[
ω
1
,
ω
2
]
\bm \omega=[\omega 1,\omega 2]
ω=[ω1,ω2]。


多分类

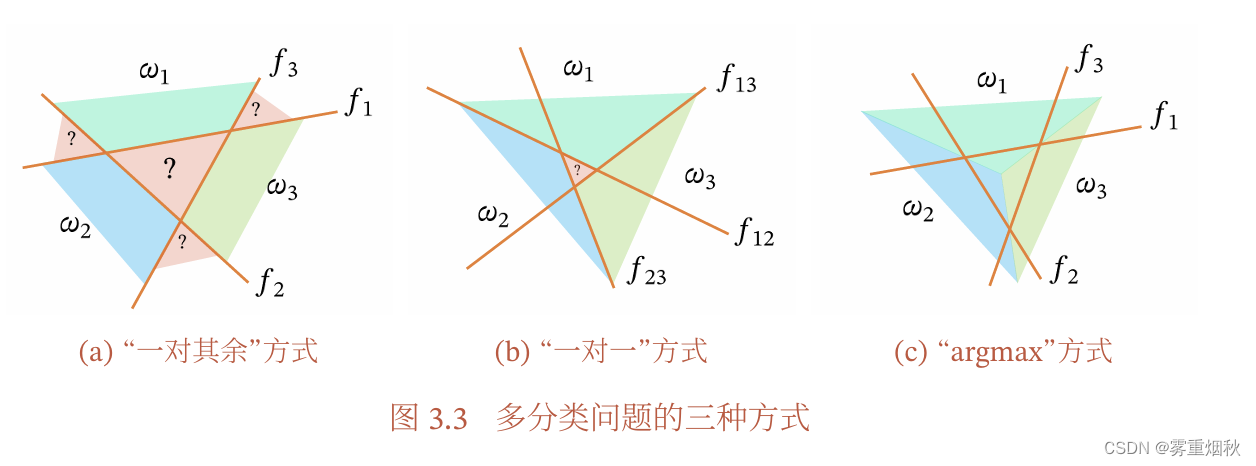
这里解释一下这幅图:
(a)如果有C个类别,那么有C个二分类器,每个二分类器有两种类别(是这个类、不是这个类),以中间区域为例,
f
1
f_1
f1显示其不属于类别1,同理,也不属于类别2、3,所以它是无法判断类别的区域。
(b)如果有C个类别,就需要
C
(
C
−
1
)
/
2
C(C-1)/2
C(C−1)/2个二分类器,每个分类器有两种类别(是这个类,是那个类),比如说
ω
2
\omega 2
ω2和
ω
3
\omega 3
ω3就训练出了一个分类器
f
2
3
f_23
f23,划分第二类或者第三类,而中间部分根据分类器投票结果得到,由于投票可能出现平票的情况,如图就是类别1、2、3各一票,因此也无法判断类别。
(c)C个分类器,但是在难以确定类别的区域,使用argmax来决策,确定为分数最高的类别。

Logistic回归


参数学习


Softmax回归


参数学习




感知器

参数学习

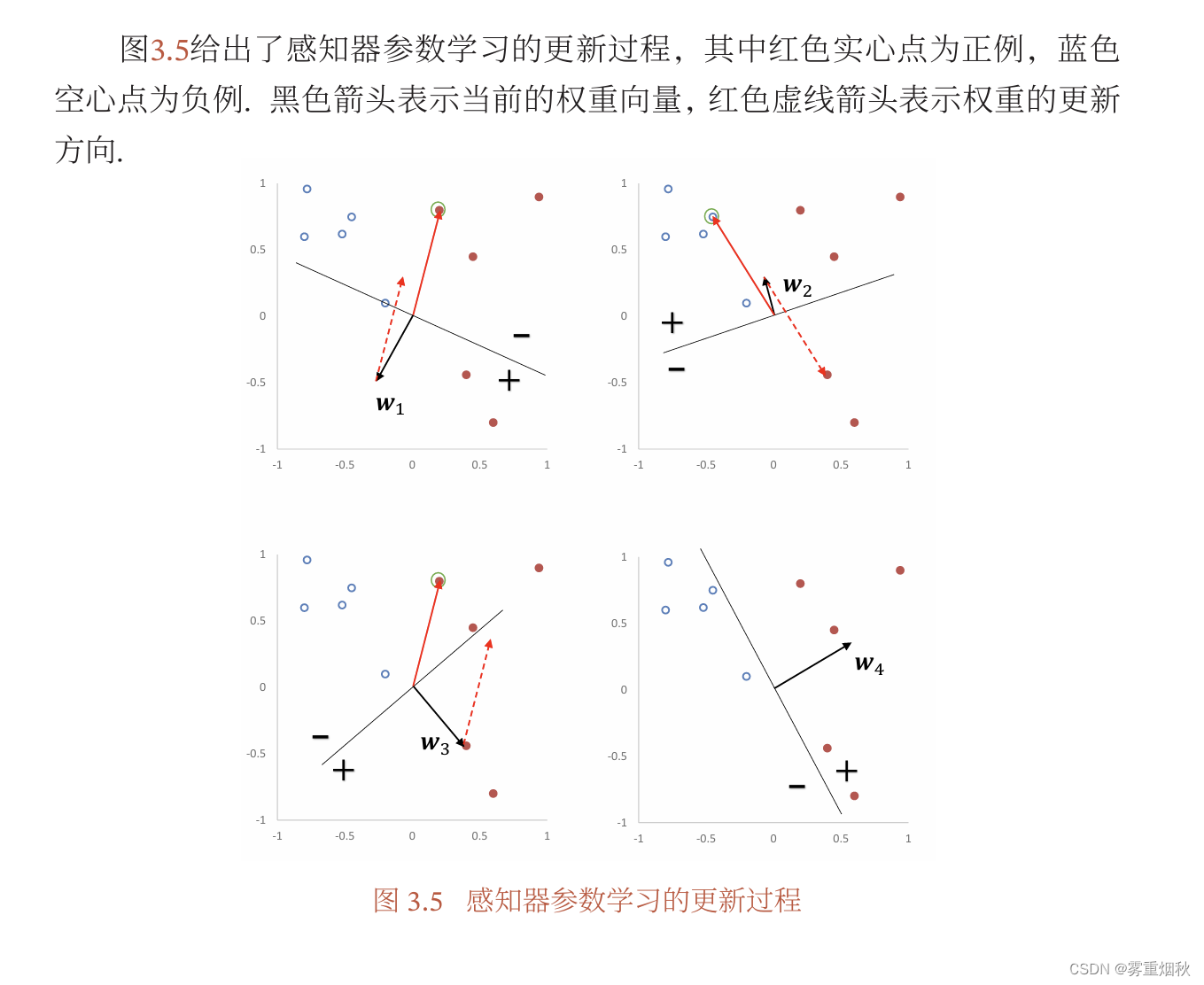
这里需要解释更新权重的过程:每次分错一个样本
(
x
,
y
)
(\bm x,y)
(x,y)时,即
y
ω
T
x
<
0
y\bm \omega^T \bm x<0
yωTx<0,用
ω
^
=
ω
+
y
x
\hat{\bm \omega} = \bm \omega+y\bm x
ω^=ω+yx来更新权重,这样的话,当再次分这个样本的时候,
y
ω
^
x
=
y
(
ω
+
y
x
)
T
x
=
y
ω
T
x
+
y
2
x
T
x
=
y
ω
T
x
+
x
T
x
>
=
y
ω
T
x
y\hat{\bm \omega} \bm x = y(\bm \omega + y\bm x)^T \bm x =y\bm \omega^T \bm x+y^2\bm x^T \bm x =y\bm \omega^T \bm x+\bm x^T \bm x>=y\bm \omega^T \bm x
yω^x=y(ω+yx)Tx=yωTx+y2xTx=yωTx+xTx>=yωTx,所以这个值会变大,最终会大于0,也就是分类正确,所以这个更新权重的方式是合理的。
这种更新参数方式和Logistic回归区别在于,后者是更新的预测和真实值的差异,所以Logistic似乎更加合理。感知器只有犯错才更新,Logistic不管是否犯错,只要与真实分布有差异,就会更新参数。

感知器的收敛性



参数平均感知器




扩展到多分类


广义感知器的收敛性


支持向量机


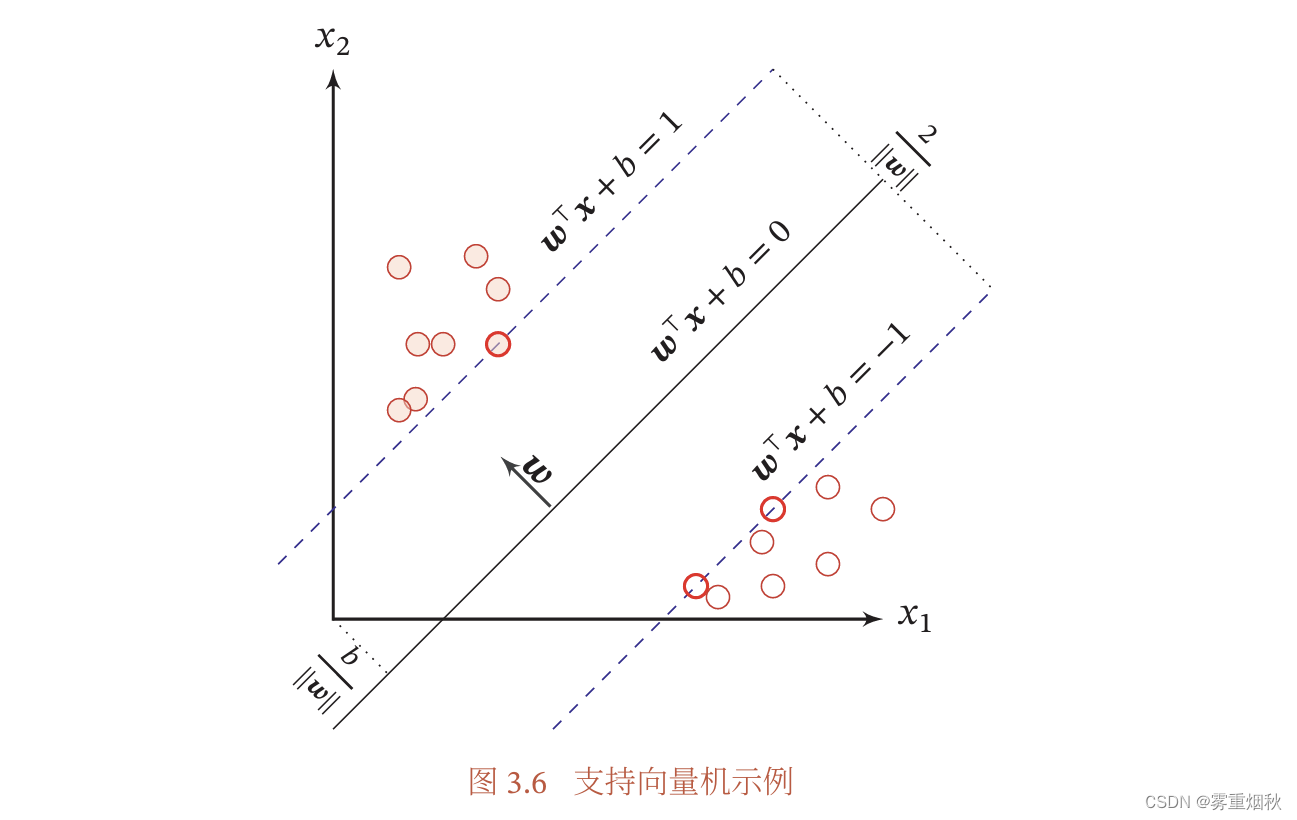
**支持向量机就是要找到一个超平面,让最短距离(间隔)最大,即数据集中所有样本到分割超平面的最短距离最大。**图中的两条虚线就是支持向量,上面的那个点到超平面的距离就是间隔,这就是最短距离,决策边界是由支持向量决定的。
参数学习



核函数

软间隔
支持向量原始定义必须让样本在特征空间线性可分,对于不满足线性可分约束的样本,需要引入松弛变量


损失函数对比

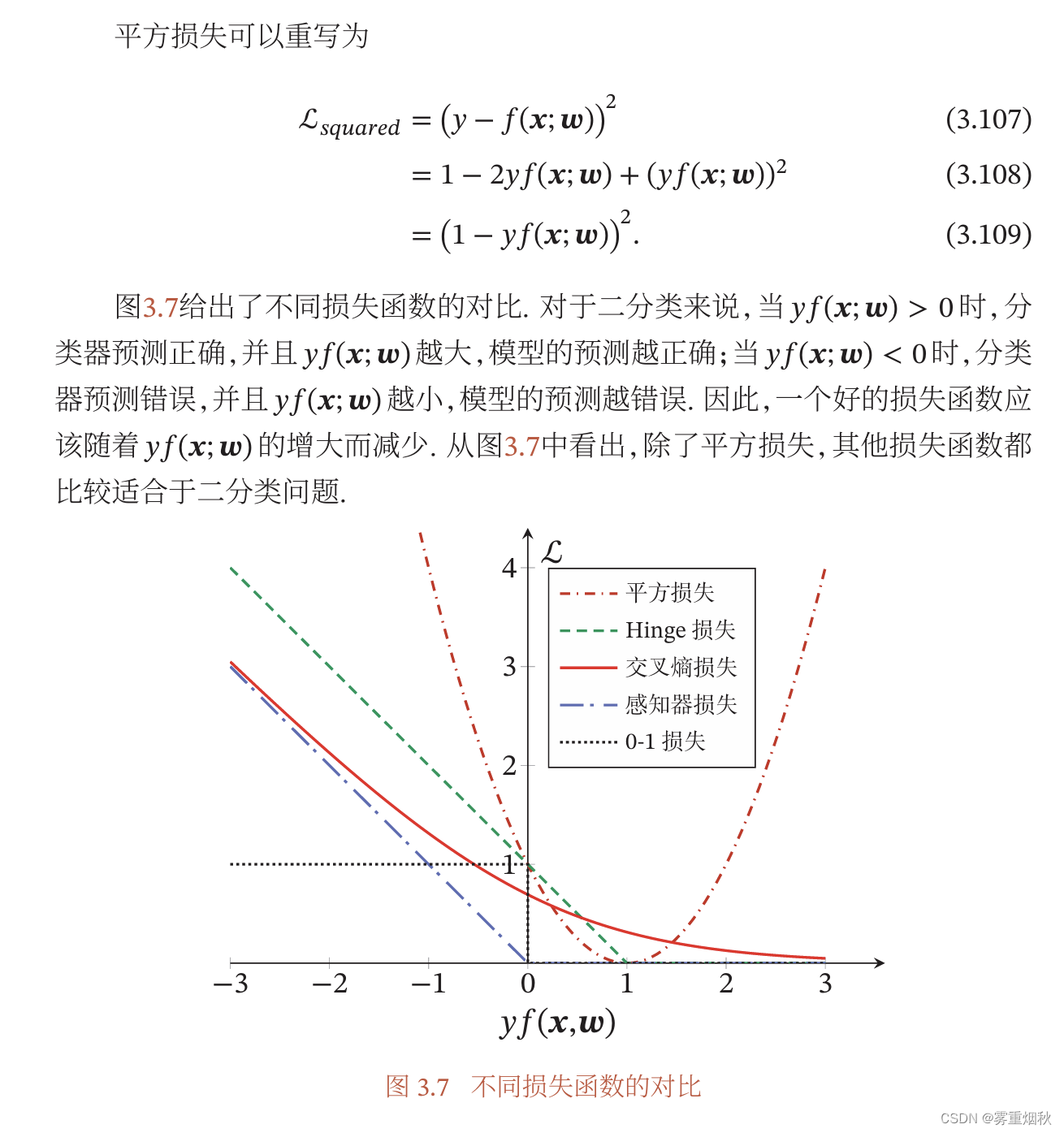
这里给出解释,这个图给出了平方损失、Hinge损失、交叉熵损失、感知器损失和0-1损失在二分类上的对比,横坐标
y
f
(
x
,
ω
)
yf(\bm x,\bm \omega)
yf(x,ω)小于0代表分类错误,大于0是分类正确,可以看到,平方损失
L
s
q
u
a
r
e
d
=
(
y
−
f
(
x
;
ω
)
)
2
=
1
−
2
y
f
(
x
;
ω
)
+
(
y
f
(
x
;
ω
)
)
2
=
(
1
−
y
f
(
x
;
ω
)
)
2
L_squared=(y-f(\bm x;\bm \omega))^2=1-2yf(\bm x;\bm \omega)+(yf(\bm x; \bm \omega))^2=(1-yf(\bm x; \bm \omega))^2
Lsquared=(y−f(x;ω))2=1−2yf(x;ω)+(yf(x;ω))2=(1−yf(x;ω))2在1左边是下降趋势,是合理的,但在1右边,命名已经分类正确并且离决策边界越来越远,但是损失函数反而上升,说明平方损失不适合二分类问题。Logistic回归的交叉熵损失求出来是公式3.104的形式,可以看出随着分类越正确,损失降低,但是即时已经划分正确了,它还是会有一部分损失,会进行参数更新。感知器损失是专门为二分类服务的,只有分错的情况才会有损失,软间隔支持向量机的损失函数相当于感知器损失函数向右平移一个单位。一个好的损失函数应该随着
y
f
(
x
,
ω
)
yf(\bm x,\bm \omega)
yf(x,ω)的增大而减少。
总结和深入阅读


习题

证明:设决策平面是
f
(
x
,
ω
)
=
ω
T
x
+
b
=
0
f(\bm x,\bm \omega)=\bm \omega^T \bm x+b=0
f(x,ω)=ωTx+b=0,对于
∀
x
1
,
x
2
∈
ω
T
x
+
b
=
0
\forall {x_1,x_2} \in \bm \omega^T \bm x+b=0
∀x1,x2∈ωTx+b=0,有
ω
T
x
1
+
b
=
ω
x
2
+
b
=
0
\bm \omega^T \bm x_1+b = \bm \omega \bm x_2+b = 0
ωTx1+b=ωx2+b=0,那么有
ω
(
x
1
−
x
2
)
=
0
\bm \omega(\bm x_1-\bm x_2)=0
ω(x1−x2)=0,说明
ω
\bm \omega
ω和向量
x
1
−
x
2
\bm {x_1-x_2}
x1−x2垂直,所以权重向量
ω
\bm \omega
ω与决策平面正交。

证明:点到平面的距离公式
d
=
∣
A
x
+
B
y
+
C
z
+
D
∣
A
2
+
B
2
+
C
2
d=\frac{|Ax+By+Cz+D|}{\sqrt{A^2+B^2+C^2}}
d=A2+B2+C2∣Ax+By+Cz+D∣,
ω
T
x
=
[
A
,
B
,
C
]
x
\bm \omega^T \bm x = [A, B, C]\bm x
ωTx=[A,B,C]x,所以
d
=
∣
f
(
x
;
ω
)
∣
∣
∣
ω
∣
∣
d=\frac{|f(\bm x; \bm \omega)|}{||\bm \omega||}
d=∣∣ω∣∣∣f(x;ω)∣。

证明:只需证
ω
c
T
(
ρ
x
1
+
(
1
−
ρ
)
x
2
)
>
ω
c
~
T
(
ρ
x
1
+
(
1
−
ρ
)
x
2
)
\bm \omega^T_c(\rho \bm x_1 + (1-\rho)\bm x_2) > \bm \omega^T_{\tilde c}(\rho \bm x_1 + (1-\rho)\bm x_2)
ωcT(ρx1+(1−ρ)x2)>ωc~T(ρx1+(1−ρ)x2),因为点
x
1
\bm x_1
x1和
x
2
\bm x_2
x2被分为类别
c
c
c,那么有
ω
c
T
x
1
>
ω
c
~
T
x
1
\bm \omega^T_c \bm x_1>\bm \omega^T_{\tilde c}\bm x_1
ωcTx1>ωc~Tx1和
ω
c
T
x
2
>
ω
c
~
T
x
2
\bm \omega^T_c \bm x_2>\bm \omega^T_{\tilde c}\bm x_2
ωcTx2>ωc~Tx2,这样有
ρ
(
ω
c
T
x
1
−
ω
c
~
T
x
1
)
>
0
,
(
1
−
ρ
)
(
ω
c
T
x
2
−
ω
c
~
T
x
2
)
>
0
\rho (\bm \omega^T_c \bm x_1-\bm \omega^T_{\tilde c}\bm x_1)>0,(1-\rho) (\bm \omega^T_c \bm x_2-\bm \omega^T_{\tilde c}\bm x_2)>0
ρ(ωcTx1−ωc~Tx1)>0,(1−ρ)(ωcTx2−ωc~Tx2)>0,因此有
ρ
(
ω
c
T
x
1
−
ω
c
~
T
x
1
)
+
(
1
−
ρ
)
(
ω
c
T
x
2
−
ω
c
~
T
x
2
)
>
0
\rho (\bm \omega^T_c \bm x_1-\bm \omega^T_{\tilde c}\bm x_1)+(1-\rho) (\bm \omega^T_c \bm x_2-\bm \omega^T_{\tilde c}\bm x_2)>0
ρ(ωcTx1−ωc~Tx1)+(1−ρ)(ωcTx2−ωc~Tx2)>0,即
ρ
ω
c
T
x
1
+
(
1
−
ρ
)
ω
c
T
x
2
>
ρ
ω
c
~
T
x
1
+
(
1
−
ρ
)
ω
c
~
T
x
2
\rho \bm \omega^T_c \bm x_1+(1-\rho) \bm \omega^T_c \bm x_2>\rho \bm \omega^T_{\tilde c}\bm x_1+(1-\rho) \bm \omega^T_{\tilde c} \bm x_2
ρωcTx1+(1−ρ)ωcTx2>ρωc~Tx1+(1−ρ)ωc~Tx2,即
ω
c
T
(
ρ
x
1
+
(
1
−
ρ
)
x
2
)
>
ω
c
~
T
(
ρ
x
1
+
(
1
−
ρ
)
x
2
)
\bm \omega^T_c (\rho \bm x_1+(1-\rho)\bm x_2)>\bm \omega^T_{\tilde c}(\rho \bm x_1+(1-\rho)\bm x_2)
ωcT(ρx1+(1−ρ)x2)>ωc~T(ρx1+(1−ρ)x2)。得证。

(1)这个其实就是“一对其余”方式的改进,一对其余是判别函数
f
c
f_c
fc将属于类别
c
c
c和不属于类别
c
c
c划分,这题的题意是将属于类别
c
c
c和属于除了
c
c
c的其他类别划分,因此每一个样本都能根据判别函数划分开,并不存在同时不属于所有类别的情况,一定是可分的。
(2)这个就是一对一方式,会出现同时属于多个类别且投票票数相等的情况,这类区域的样本是不能划分类别的,因此该数据集不一定是线性可分的。
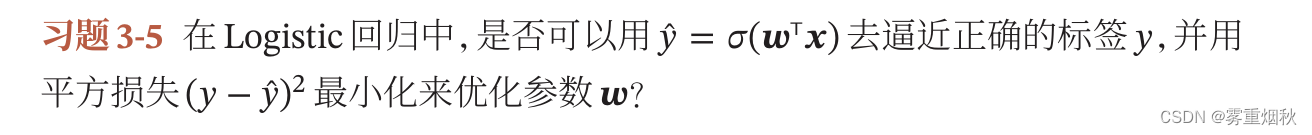
平方损失可以用于分类问题,但并不适合用于分类问题,由之前的损失函数对比图可以看出来,对于分类正确的情况,平方损失会增加,而且平方损失在Logistic回归的情况是非凸函数,容易收敛到局部最优。Logistic回归的激活函数一般是Sigmoid函数,当用平方损失时,有
L
=
1
2
(
y
^
−
y
)
2
L=\frac{1}{2}(\hat y-y)^2
L=21(y^−y)2,对权重的导数为
∂
L
∂
ω
=
(
y
^
−
y
)
σ
′
x
\frac{\partial L}{\partial \bm \omega}=(\hat y-y)\sigma'\bm x
∂ω∂L=(y^−y)σ′x,那么进行权重更新的公式就为
ω
=
ω
−
μ
∂
L
∂
ω
=
ω
−
μ
(
y
^
−
y
)
σ
′
x
\bm \omega=\bm \omega-\mu\frac{\partial L}{\partial \bm \omega}=\bm \omega - \mu(\hat y -y)\sigma'\bm x
ω=ω−μ∂ω∂L=ω−μ(y^−y)σ′x。而Sigmoid函数在横坐标大的时候导数小,这样和参数更新的目标是相反的,在损失大的时候,参数更新反而慢,损失小的时候,梯度反而大。

公式3.39为
R
(
W
)
=
−
1
N
∑
n
=
1
N
(
y
(
n
)
)
T
l
o
g
y
^
(
n
)
R(W)=-\frac{1}{N}\sum^N_{n=1} (y^{(n)})^Tlog\hat y^{(n)}
R(W)=−N1∑n=1N(y(n))Tlogy^(n),加入正则化后:
R
(
W
)
=
−
1
N
∑
n
=
1
N
(
y
(
n
)
)
T
l
o
g
y
^
(
n
)
+
λ
W
T
W
R(W)=-\frac{1}{N}\sum^N_{n=1} (y^{(n)})^Tlog\hat y^{(n)}+\lambda W^TW
R(W)=−N1∑n=1N(y(n))Tlogy^(n)+λWTW,对权重的导数为:
∂
R
(
W
)
∂
W
=
−
1
N
∑
n
=
1
N
(
y
^
(
n
)
−
y
(
n
)
)
x
(
n
)
+
2
λ
W
\frac{\partial {R(W)}}{\partial W}=-\frac{1}{N}\sum^N_{n=1} (\hat y^{(n)}-y^{(n)})x^{(n)}+2 \lambda W
∂W∂R(W)=−N1∑n=1N(y^(n)−y(n))x(n)+2λW,更新参数的时候为
W
=
W
+
α
1
N
∑
n
=
1
N
(
y
^
(
n
)
−
y
(
n
)
)
x
(
n
)
−
2
λ
W
W = W+\alpha \frac{1}{N}\sum^N_{n=1} (\hat y^{(n)}-y^{(n)})x^{(n)}-2 \lambda W
W=W+αN1∑n=1N(y^(n)−y(n))x(n)−2λW。可以看出,加入正则化项之后,在更新参数时每次需要减去
2
λ
W
2\lambda W
2λW,使得参数不会太大,便不会造成溢出之类的错误发生,同时也会抑制过拟合。


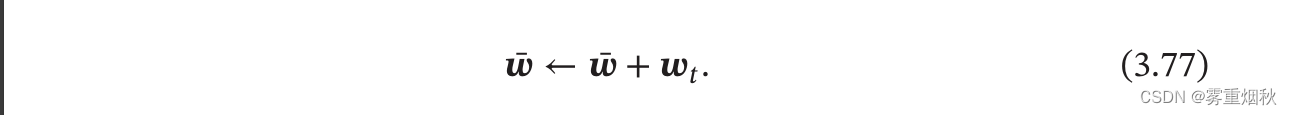
设预测错误的样本有
K
K
K个,并且设选取到这些样本时的迭代次数为
t
k
t_k
tk,那么根据算法3.2的步骤,可以计算出:
ω
=
y
1
x
1
+
y
2
x
2
+
.
.
.
+
y
k
x
k
\bm \omega = y_1\bm x_1+y_2\bm x_2+...+y_k \bm x_k
ω=y1x1+y2x2+...+ykxk,
u
=
t
1
y
1
x
1
+
t
2
y
2
x
2
+
.
.
.
+
t
k
y
k
x
k
u=t_1y_1\bm x_1+t_2y_2\bm x_2+...+t_ky_k\bm x_k
u=t1y1x1+t2y2x2+...+tkykxk,因此,
ω
‾
=
ω
−
1
T
u
=
y
1
x
1
+
y
2
x
2
+
.
.
.
+
y
k
x
k
−
1
T
(
t
1
y
1
x
1
+
t
2
y
2
x
2
+
.
.
.
+
t
k
y
k
y
k
)
=
T
−
t
1
T
y
1
x
1
+
T
−
t
2
T
y
2
x
2
+
.
.
.
+
T
−
t
k
T
y
k
x
k
\overline \omega=\omega-\frac{1}{T}u=y_1\bm x_1+y_2\bm x_2+...+y_k\bm x_k-\frac{1}{T}(t_1y_1\bm x_1+t_2y_2\bm x_2+...+t_ky_k\bm y_k)=\frac{T-t_1}{T} \bm y_1\bm x_1+\frac{T-t_2}{T}y_2\bm x_2+...+\frac{T-t_k}{T}y_k \bm x_k
ω=ω−T1u=y1x1+y2x2+...+ykxk−T1(t1y1x1+t2y2x2+...+tkykyk)=TT−t1y1x1+TT−t2y2x2+...+TT−tkykxk。
而根据公式3.77,
ω
=
∑
t
=
1
T
ω
t
\bm \omega = \sum^T_{t=1} \omega_t
ω=∑t=1Tωt,
ω
t
=
∑
i
=
1
k
<
=
t
x
i
y
i
ω
‾
=
1
T
ω
\omega_t = \sum^{k<=t}_{i=1}x_iy_i\overline \omega=\frac{1}{T}\omega
ωt=∑i=1k<=txiyiω=T1ω。
ω
=
(
x
1
y
1
+
.
.
.
+
x
1
y
1
)
+
(
x
1
y
1
+
x
2
y
2
+
.
.
.
+
x
1
y
1
+
x
2
y
2
)
+
.
.
.
+
(
∑
i
=
1
k
x
i
y
i
+
.
.
.
+
∑
i
=
1
k
x
i
y
i
)
\bm \omega=(\bm x_1 y_1+...+\bm x_1 y_1)+(\bm x_1 y_1+\bm x_2 y_2+...+\bm x_1 y_1+\bm x_2 y_2)+...+(\sum^k_{i=1}\bm x_iy_i+...+\sum^k_{i=1}\bm x_i y_i)
ω=(x1y1+...+x1y1)+(x1y1+x2y2+...+x1y1+x2y2)+...+(∑i=1kxiyi+...+∑i=1kxiyi)。式中,当第二个预测错误的样本被选取时才开始加
x
2
y
2
\bm x_2 y_2
x2y2,也就是说到达
t
2
t_2
t2时刻时才开始加,其中
x
i
y
i
\bm x_i y_i
xiyi类似,到达
t
i
t_i
ti时刻时开始加,因此
x
i
y
i
\bm x_i y_i
xiyi共相加了
T
−
t
i
T-t_i
T−ti次
所以
ω
=
(
T
−
t
i
)
x
1
y
1
+
(
T
−
t
2
)
x
2
y
2
+
.
.
.
+
(
T
−
t
k
)
x
k
y
k
\bm \omega = (T-t_i)\bm x_1 y_1+(T-t_2)\bm x_2y_2+...+(T-t_k)\bm x_k y_k
ω=(T−ti)x1y1+(T−t2)x2y2+...+(T−tk)xkyk,
ω
‾
=
1
T
ω
\overline \omega=\frac{1}{T} \omega
ω=T1ω,得证。

这里不证明了,记住这个结论。
后续的习题之后有需要的时候再做。

![[图的搜索]5.图解狄克斯特拉算法及其代码演示](https://img-blog.csdnimg.cn/direct/f93a9eca90f2439aa7b11804b68239bb.png)