020.有效的括号，用栈来解决的 Java 版 LeetCode 刷题笔记

news2025/1/11 22:47:31

题意

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

难度

简单

示例

输入：s = "()"
输出：true

输入：s = "()[]{}"
输出：true

输入：s = "(]"
输出：false

输入：s = "([)]"
输出：false

输入：s = "{[]}"
输出：true
复制代码

分析 1

对于括号的匹配，我们可以利用栈这个数据结构来实现。为什么呢？

我们先来看百度百科对栈的定义。

栈（stack）又名堆栈，一种限定仅在表尾进行插入/删除的线性表。一端被称为栈顶，另一端称为栈底。向一个栈插入新元素称作入栈，它会把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素称作出栈，它会把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素

然后我们来分析这道题。

要判断当前这个右括号是否跟它未匹配过的最近的左括号相匹配，我们可以先把这个左括号压入栈中，匹配成功后再把这个括号从栈中弹出。

1、遇到左括号出栈

2、遇到右括号入栈

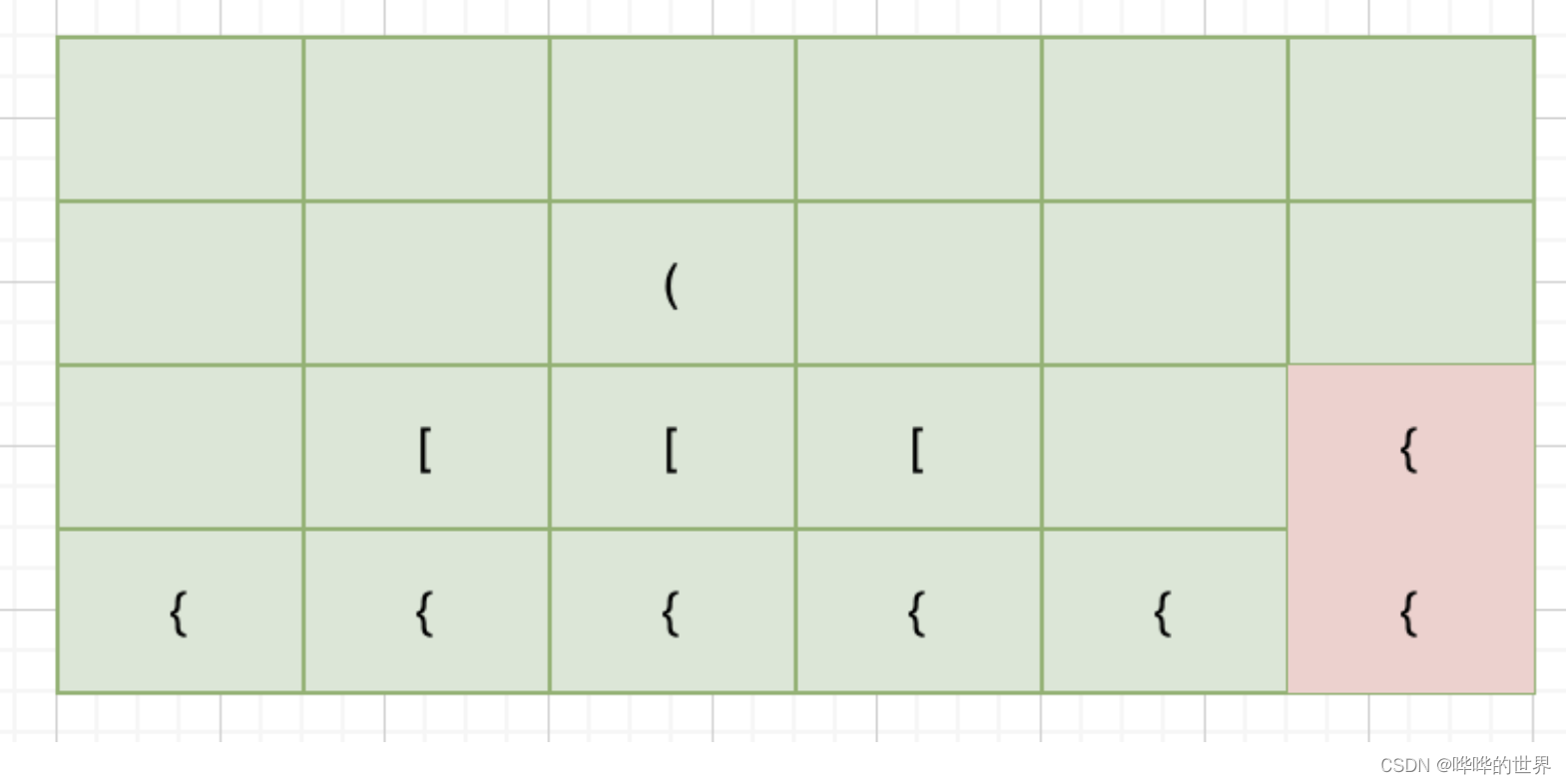
来看题解，也很简单：

class Solution {
    public boolean isValid(String s) {
        // 创建一个栈来存放括号
        Stack<Character> stack = new Stack<>();

        // 遍历字符串中的每个字符
        for (char c : s.toCharArray()) {
            // 如果是开括号，压入栈中
            if (c == '(' || c == '[' || c == '{') {
                stack.push(c);
            } else {
                // 如果是闭括号，检查栈是否为空，以及栈顶元素是否与之匹配
                if (stack.isEmpty()) {
                    return false; // 栈为空，说明没有对应的开括号
                }

                // 检查栈顶元素
                char top = stack.pop();
                if ((c == ')' && top != '(') || 
                    (c == ']' && top != '[') || 
                    (c == '}' && top != '{')) {
                    return false; // 栈顶元素与当前闭括号不匹配
                }
            }
        }

        // 如果栈为空，说明所有括号都正确匹配
        return stack.isEmpty();
    }
}
复制代码

①、首先我们创建一个栈 Stack来存放括号，然后遍历字符串中的每个字符。

②、如果当前字符是开括号（包括(、[、{），我们就把它压入栈中。

③、如果当前字符是闭括号（包括)、]、}），我们就检查栈是否为空，以及栈顶元素是否与之匹配。

空的话，肯定不匹配，直接返回。

倘若匹配成功，则继续向后匹配，如果不成功，则必然是个不合法的括号序列，直接返回 false。

而匹配成功仅限于以下三种情况：

当前第i位字符为(，且栈顶元素为)
当前第i位字符为[，且栈顶元素为]
当前第i位字符为{，且栈顶元素为}

④、最后，如果栈为空，说明所有括号都正确匹配，返回 true，否则返回 false。

来看执行效率：

分析 2

Stack 是线程安全的类，它的 push、pop、peek 等方法都是同步的，那么我们能不能用一个非线程安全的类来代替呢？

答案是肯定的，我们可以用 ArrayDeque来代替 Stack。

class Solution {
    public boolean isValid(String s) {
        // 使用 ArrayDeque 作为栈使用
        Deque<Character> stack = new ArrayDeque<>();

        // 遍历字符串
        for (char c : s.toCharArray()) {
            // 如果是开括号，压入栈中
            if (c == '(' || c == '[' || c == '{') {
                stack.push(c);
            } else {
                // 如果是闭括号，检查栈是否为空，以及栈顶元素是否与之匹配
                if (stack.isEmpty()) {
                    return false; // 栈为空，说明没有对应的开括号
                }

                // 检查栈顶元素
                char top = stack.pop();
                if ((c == ')' && top != '(') || 
                    (c == ']' && top != '[') || 
                    (c == '}' && top != '{')) {
                    return false; // 栈顶元素与当前闭括号不匹配
                }
            }
        }

        // 如果栈为空，说明所有括号都正确匹配
        return stack.isEmpty();
    }
}
复制代码

代码几乎一样，只是换了不同的容器。题解效率大差不差，内存消耗上提升了一点。