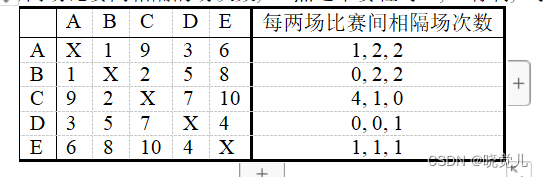
你所在的年级有5个班,每班一支球队在同一块场地上进行单循环赛, 共要进行10场比赛. 如何安排赛程使对各队来说都尽量公平呢. 下面是随便安排的一个赛程: 记5支球队为A, B, C, D, E,在下表左半部分的右上三角的10个空格中, 随手填上1,2,10, 就得到一个赛程, 即第1场A对B, 第2场B对C, , 第10场C对E. 为方便起见将这些数字沿对角线对称地填入左下三角.
这个赛程的公平性如何呢, 不妨只看看各队每两场比赛中间得到的休整时间是否均等. 表的右半部分是各队每两场比赛间相隔的场次数, 显然这个赛程对A, E有利, 对D则不公平.
从上面的例子出发讨论以下问题:
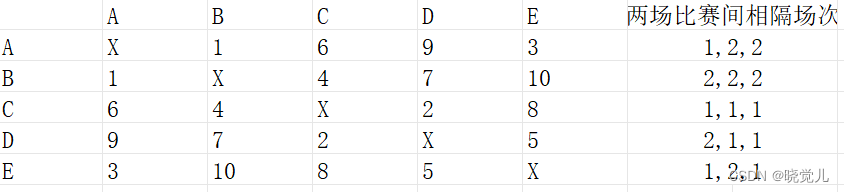
1)对于5支球队的比赛, 给出一个各队每两场比赛中间都至少相隔一场的赛程.
2)当n支球队比赛时, 各队每两场比赛中间相隔的场次数的上限是多少.
3)在达到2) 的上限的条件下, 给出n=8, n=9的赛程, 并说明它们的编制过程.
问题一
问题二
偶数个球队:各队每两场比赛中间相隔的场次数的最小值的上限是
n
2
−
1
\dfrac{n}{2}-1
2n−1
奇数个球队:各队每两场比赛中间相隔的场次数的最小值的上限是
n
−
3
2
\dfrac{n-3}{2}
2n−3
向下取整后,不分奇偶,都是
n
−
3
2
\dfrac{n-3}{2}
2n−3
式子来源:
R
≤
(
n
−
3
)
/
2
R\le (n-3)/2
R≤(n−3)/2,
R
R
R为间隔
问题三
编制过程:(暂不给予说明)
#include <iostream>
#include <map>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 20;
int n,r,nx,mr;
vector<pair<int,int> >v(200);
vector<int>chose(200);//选择
int interval[N];//间隔
int ans[N][N];//答案矩阵
//优化结构
map<pair<int,int>,int>mv;//对局->选择
int maxn[N];//当前球队比赛场次最大值(球队上次比赛的场次)
void f(int);
inline void print_ans();
int main(){ // n=12 运行时间突变
cin >> n; // n个球队
r = (n-3)/2;//间隔下线(下限)
nx = (n-1)*n/2;//(n-1)+(n-2)+...+1
//step1. 列出每一个对局(小数在前),并初始化对局
int x = 1;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
v[x++] = make_pair(i,j);
mv[{i,j}]=x-1;
}
}
for(int i=1;i<=n;i++){
interval[i] = -1;
maxn[i] = -1;
}
//step2. 初始化选择
if(n%2==0){
mr = r+3;//间隔上限
int k = 1;
//12 34 ... n-1 n
for(int i=1;i<=n-1;i+=2){
ans[i][i+1] = ans[i+1][i] = (i+1)/2;
maxn[i]=maxn[i+1] = k;
chose[k++]=mv[{i,i+1}];
}
for(int i=1;i<=n-5;i+=4){
for(int j=0;j<2;j++){
//ans[i+j][i+j+2] = ans[i+j+2][i+j] = k;
ans[i+j][(i+j+2+n)%n] = ans[(i+j+2+n)%n][i+j] = k;
maxn[i+j]=maxn[(i+j+2+n)%n] = k;
chose[k++]=mv[{i+j,(i+j+2+n)%n}];
}
}
f(k);
}
else{
mr = r+2;//间隔上限
int k = 1;
//12 34 ... n-2 n-1
for(int i=1;i<=n-2;i+=2){
ans[i][i+1] = ans[i+1][i] = (i+1)/2;
maxn[i]=maxn[i+1] = k;
chose[k++]=mv[{i,i+1}];
}
f(k);
}
//print_ans();
return 0;
}
bool flag = false;
void f(int x){
if(flag || x == nx+1){
if(!flag)
print_ans();
flag = true;
//all return
//cout ans
return ;
}
//step3. 算间隔,取出必选(可选)的列表(对局列表)
vector<int>must_chose;
#if 0
for(int i=1;i<=r+1;i++){// x x-1 x-2 .. x-r
pair<int,int> pi_t = v[chose[x-i]];
interval[pi_t.first] = interval[pi_t.second] = i;
}
#endif
bool m_or_ke = false;//false 表示 是可选列表, 反之是必选
vector<int>must_n;
vector<int>no_n;
for(int i=1;i<=n;i++){
if(maxn[i]==-1){//没被选过
must_n.push_back(i);
continue;
}
if(m_or_ke){//必选已经出来了
if(x-maxn[i]>mr)must_n.push_back(i);//直接加必选
if(x-maxn[i]<=r)no_n.push_back(i);//不可选
continue;
}
if(x-maxn[i]>mr){
if(!m_or_ke)must_n.clear();
m_or_ke = true;
must_n.push_back(i);
}
else if(x-maxn[i]>r){
must_n.push_back(i);
}
else{
no_n.push_back(i);//不可选
}
}
//预处理
bool mn_[n+1];
for(int i=1;i<=n;i++)mn_[i]=false;
for(auto xx:must_n)mn_[xx]=true;
for(auto xx:no_n)mn_[xx]=false;
//must_n -> must_chose
//for(int i=1;i<=nx;i++){//可优化
// if(mn_[v[i].first]&&mn_[v[i].second])must_chose.push_back(i);
//}
for(int i=1;i<=n;i++){//优化后
if(!mn_[i])continue;
for(int j=i+1;j<=n;j++){
if(mn_[j]){
must_chose.push_back(mv[{i,j}]);
}
}
}
int mi = must_chose.size();
for(int i=0;i<mi;i++){
//check
if(ans[v[must_chose[i]].first][v[must_chose[i]].second])continue;
//chose
chose[x] = must_chose[i];
ans[v[must_chose[i]].first][v[must_chose[i]].second] = x;
ans[v[must_chose[i]].second][v[must_chose[i]].first] = x;
int vf_maxn = maxn[v[must_chose[i]].first];//备份
int vs_maxn = maxn[v[must_chose[i]].second];
maxn[v[must_chose[i]].first] = maxn[v[must_chose[i]].second] = x;
f(x+1);
//cut chose
ans[v[must_chose[i]].first][v[must_chose[i]].second] = 0;
maxn[v[must_chose[i]].first] = vf_maxn;
maxn[v[must_chose[i]].second] = vs_maxn;
}
}
inline void print_ans(){
for(int i=1;i<=n;i++){
vector<int>v1;
for(int j=1;j<=n;j++){
cout << ans[i][j] << ' ';
v1.push_back(ans[i][j]);
}
sort(v1.begin(),v1.end());
cout << ',';
for(int j=2;j<n;j++){
cout << v1[j]-v1[j-1]-1 << ' ';
}
cout << '\n';
}
return ;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
cout << ans[i][j] << ' ';
cout << '\n';
}
}
代入n=9 / n=8答案可出