数据规模->时间复杂度
<=10^4 😮(n^2)
<=10^7:o(nlogn)
<=10^8:o(n)
10^8<=:o(logn),o(1)
内容
1)爬楼梯、打家劫舍问题
2)0-1,多重,完全,二维被动背包问题
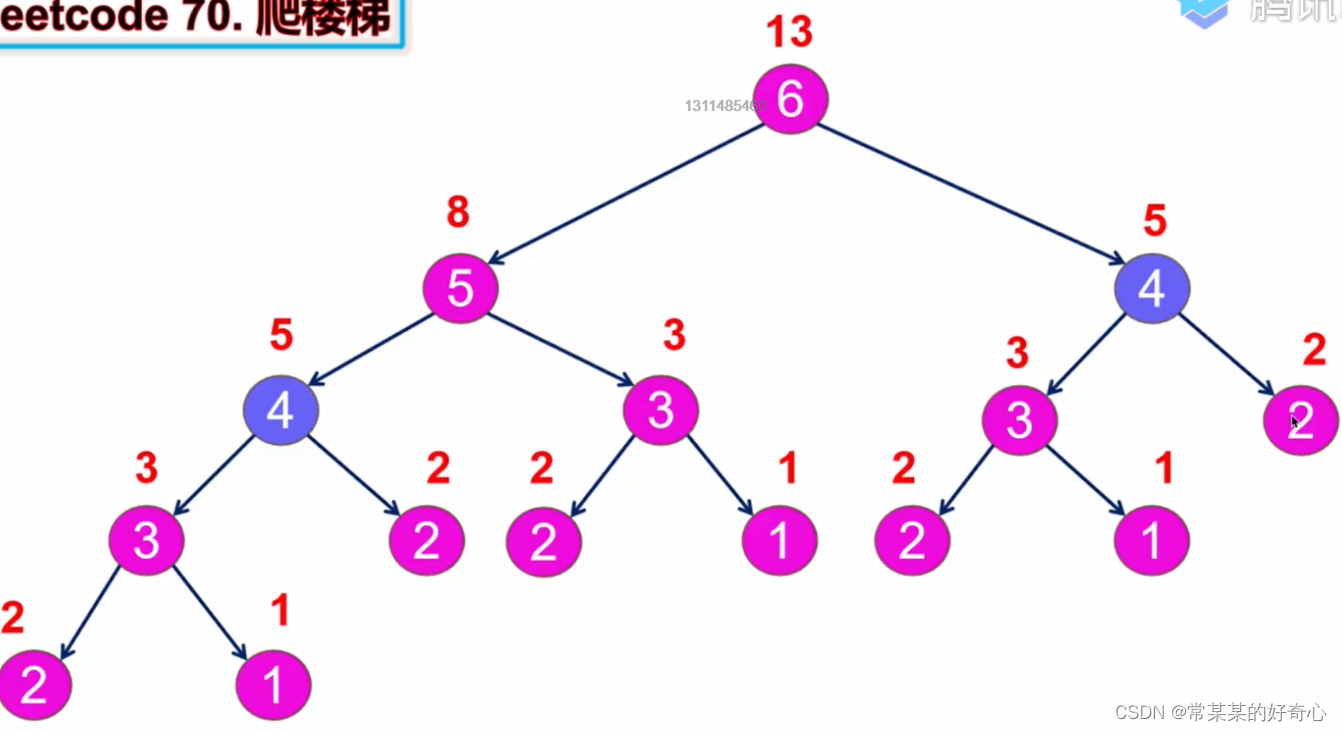
lc 70【剑指 10 - 2】【top100】: 爬楼梯
https://leetcode.cn/problems/climbing-stairs/
提示:
1 <= n <= 45
#方案一:dfs+记忆化
class Solution:
def climbStairs(self, n: int) -> int:
memo=[-1]*(n+1)
def dfs(n):
if n==1:return 1
if n==2:return 2
if memo[n]!=-1:return memo[n]
#
memo[n]=dfs(n-1)+dfs(n-2) #left+right
return memo[n]
return dfs(n)
#方案二:dp+压缩
class Solution:
def climbStairs(self, n: int) -> int:
dp=[-1]*(n+1) #走到i台阶,对应的方法数量
dp1,dp2=1,2
#[n-1]+1->[n],[n-2]+2->[n]
#(注意([n-1]+1)已存在[n-2],所以[n-2]+1+1等价于[n-2]+2)
for i in range(3,n+1):
dp1=dp2
dp2=dp1+dp2
return dp2
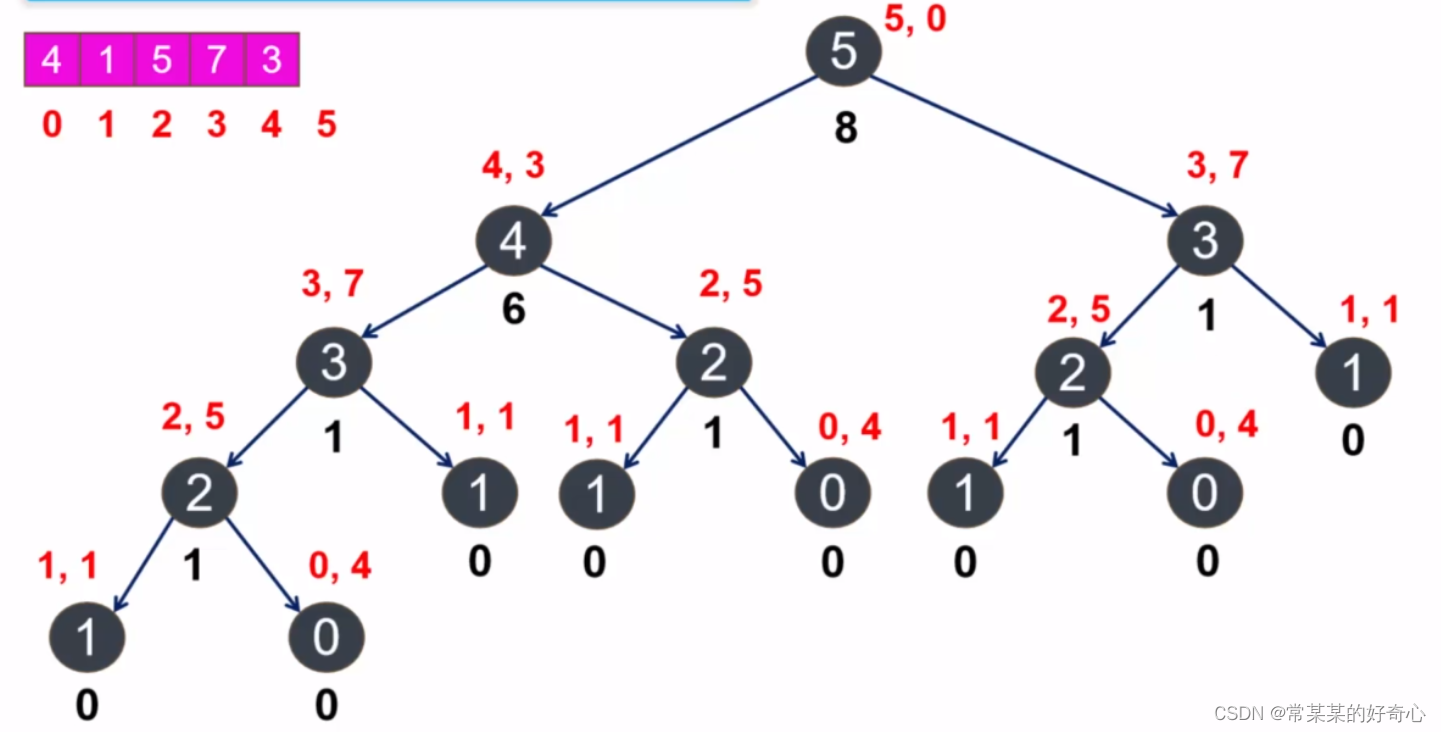
lc 746【剑指 088】:使用最小花费爬楼梯
https://leetcode.cn/problems/min-cost-climbing-stairs/
提示:
2 <= cost.length <= 1000
0 <= cost[i] <= 999
#方案一:回溯+dfs
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n=len(cost)
memo=[-1]*(n+1)
def dfs(i):
if i==0 or i==1:return 0 #从下标为 0 或下标为 1 的台阶开始爬楼梯,不需要体力值,只是从0->1或者0->2,需要cost[i]体力值
if memo[i]!=-1:return memo[i]
#
memo[i]=min(dfs(i-1)+cost[i-1],dfs(i-2)+cost[i-2])#表示爬到i-1的最低花费+cost[i-1]->爬到i
return memo[i]
return dfs(n)
#方案二:dp+压缩
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n=len(cost)
prev=curr=0
for i in range(2,n+1):
tmp=curr
curr=min(curr+cost[i-1],prev+cost[i-2])
prev=tmp
return curr
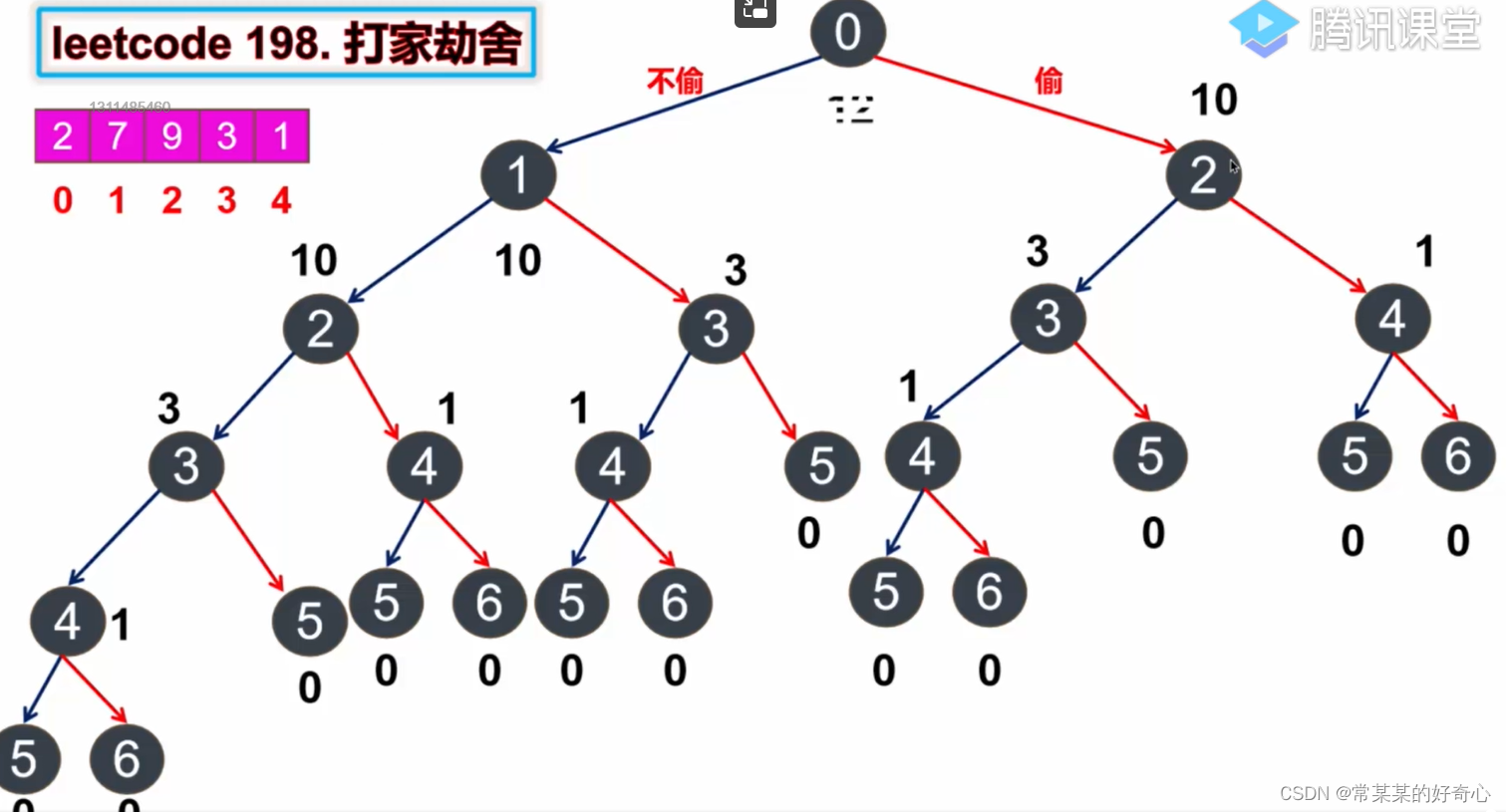
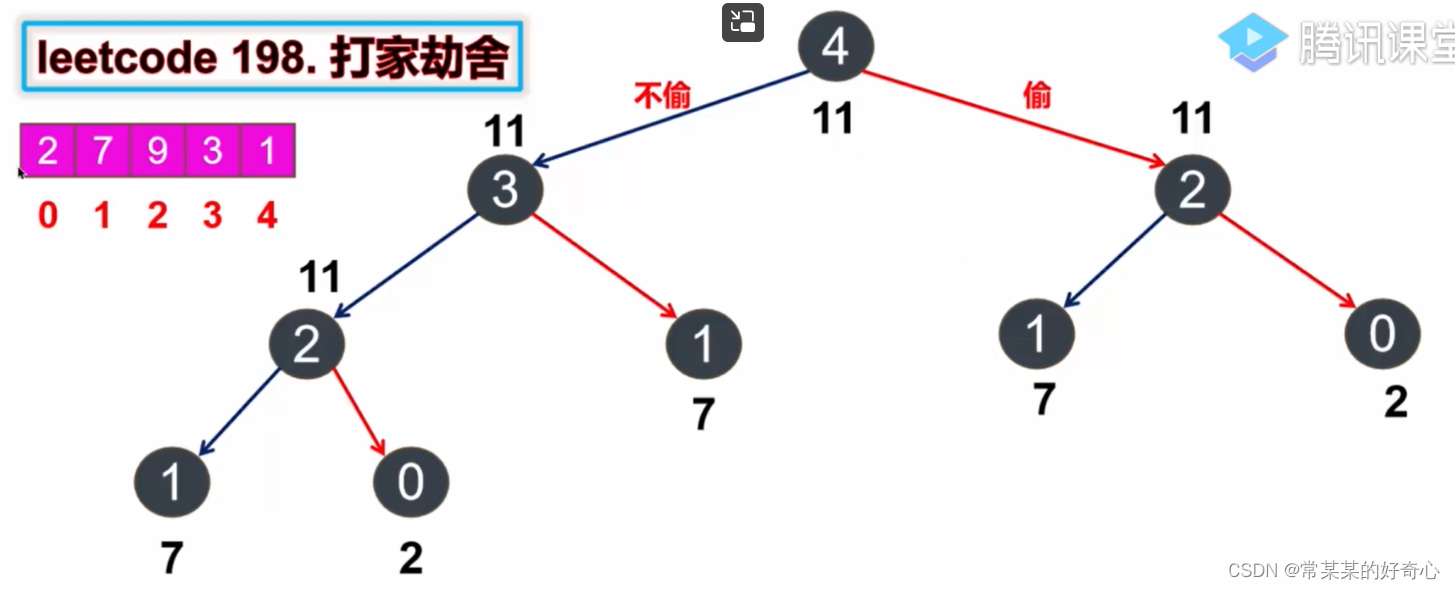
lc 198【剑指 089】【top100】:打家劫舍
https://leetcode.cn/problems/house-robber/
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 400
#方案一:回溯+记忆化
#写法一
class Solution:
def rob(self, nums: List[int]) -> int:
n=len(nums)
memo=[-1]*n # memo[i]:偷盗[i, nums.length - 1],包括i户(偷/不偷),区间房子得到的最大金额
def dfs(i):
if i>=n:return 0
if memo[i]!=-1:return memo[i]
#
memo[i]=max(dfs(i+1),dfs(i+2)+nums[i])
return memo[i]
return dfs(0)
#写法二
class Solution:
def rob(self, nums: List[int]) -> int:
n=len(nums)
memo=[-1]*n
def dfs(i):
if i<0:return 0
if memo[i]!=-1:return memo[i] #偷到i户,包括i户(偷/不偷),所能获得的最大金额
#
memo[i]=max(dfs(i-1),dfs(i-2)+nums[i])
return memo[i]
return dfs(n-1)
#方案二:dp+压缩
class Solution:
def rob(self, nums: List[int]) -> int:
n=len(nums)
if n==1:return nums[0]
dp=[-1]*n
prev=curr=0
for i in range(n):
tmp=curr
curr=max(prev+nums[i],curr)
prev=tmp
return curr
lc 213【剑指 090】:打家劫舍 II
https://leetcode.cn/problems/house-robber-ii/
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
class Solution:
def rob(self, nums: List[int]) -> int:
n=len(nums)
if n==1:return nums[0]
def rob1(i,j):
dp=[-1]*n
#
prev=curr=0
for k in range(i,j+1):
tmp=curr
curr=max(prev+nums[k],curr)
prev=tmp
return curr
return max(rob1(0,n-2),rob1(1,n-1)) #key:
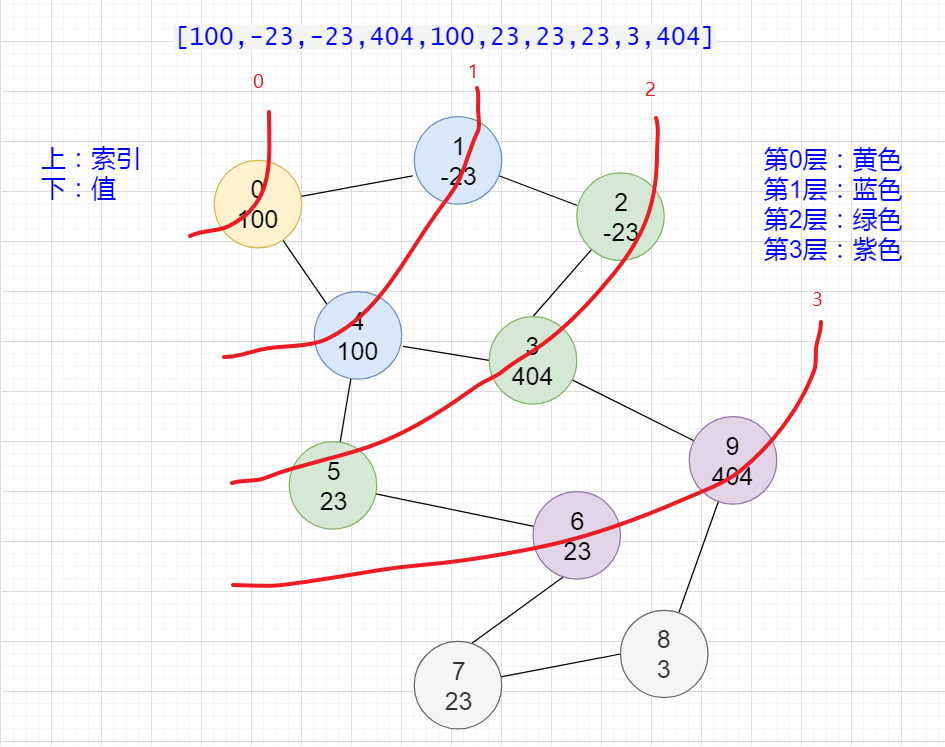
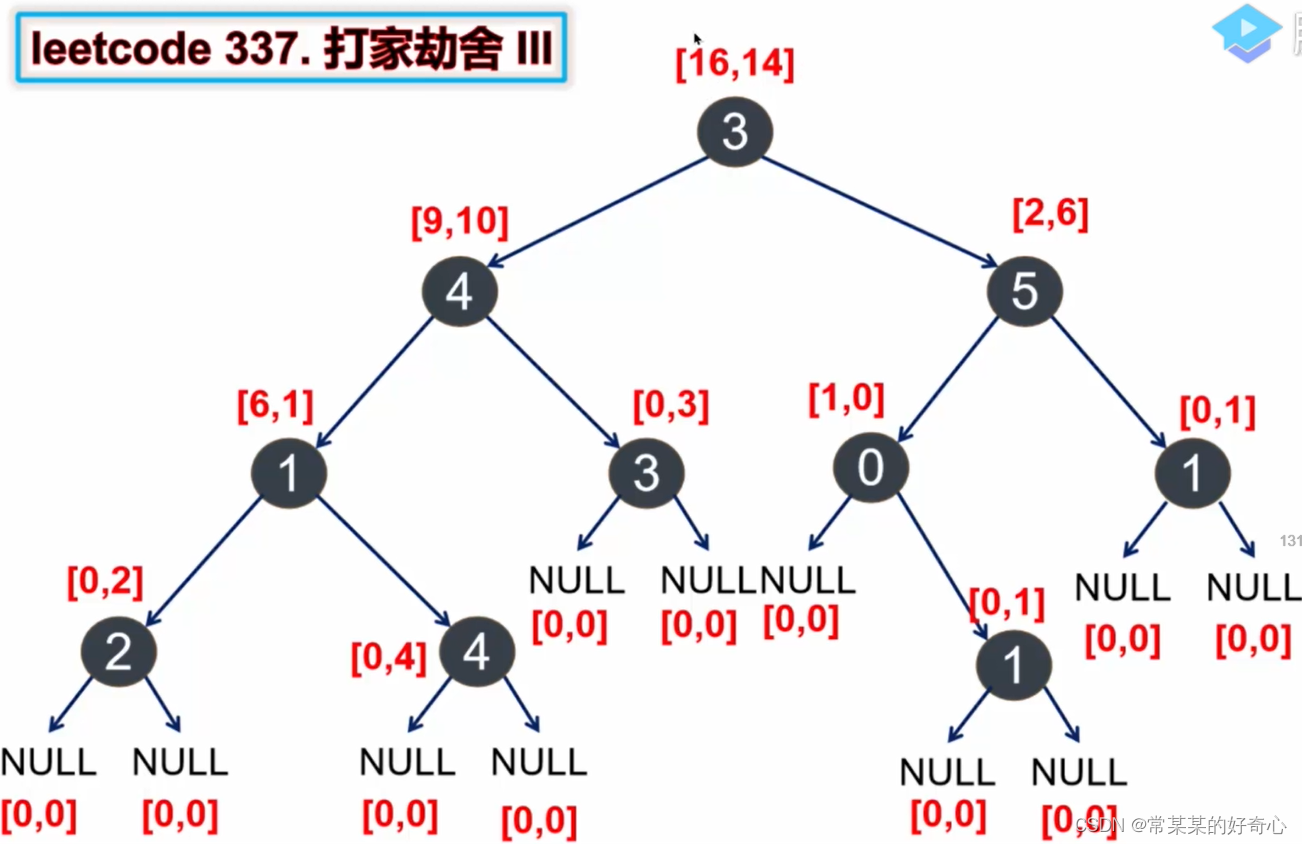
lc 337【top100】:打家劫舍 III
https://leetcode.cn/problems/house-robber-iii/
提示:
树的节点数在 [1, 10^4] 范围内
0 <= Node.val <= 10^4
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
def dfs(node):
if not node:return [0,0]
#
left,right=dfs(node.left),dfs(node.right)
#key:1)当不考虑当前节点,则在子节点中寻找到最优组合分(key-key-key)
#2)当考虑当前节点时,则累加在不选子节点的情况下,获得的最优分
res=[0]*2
res[0]=max(left[0],left[1])+max(right[0],right[1])
res[1]=left[0]+right[0]+node.val
return res
ans=dfs(root)
return max(ans[0],ans[1])
0 - 1 背包问题:每种背包只能取一次
#方案一:dfs-前序
def knapsack01(w, v, C):
maxValue = float('-inf')
def dfs(start,remain_w,curr_value):
nonlocal maxValue
maxValue=max(maxValue,curr_value) #处理当前节点
#处理子节点
for i in range(start,len(w)):
child_i=i+1
#剪枝
if child_i==len(w):continue
if remain_w-w[child_i]<0:continue
dfs(child_i,remain_w-w[child_i],curr_value+v[child_i])
dfs(-1, C, 0)
return maxValue
print(knapsack01([3,4,5],[15,14,12],10))
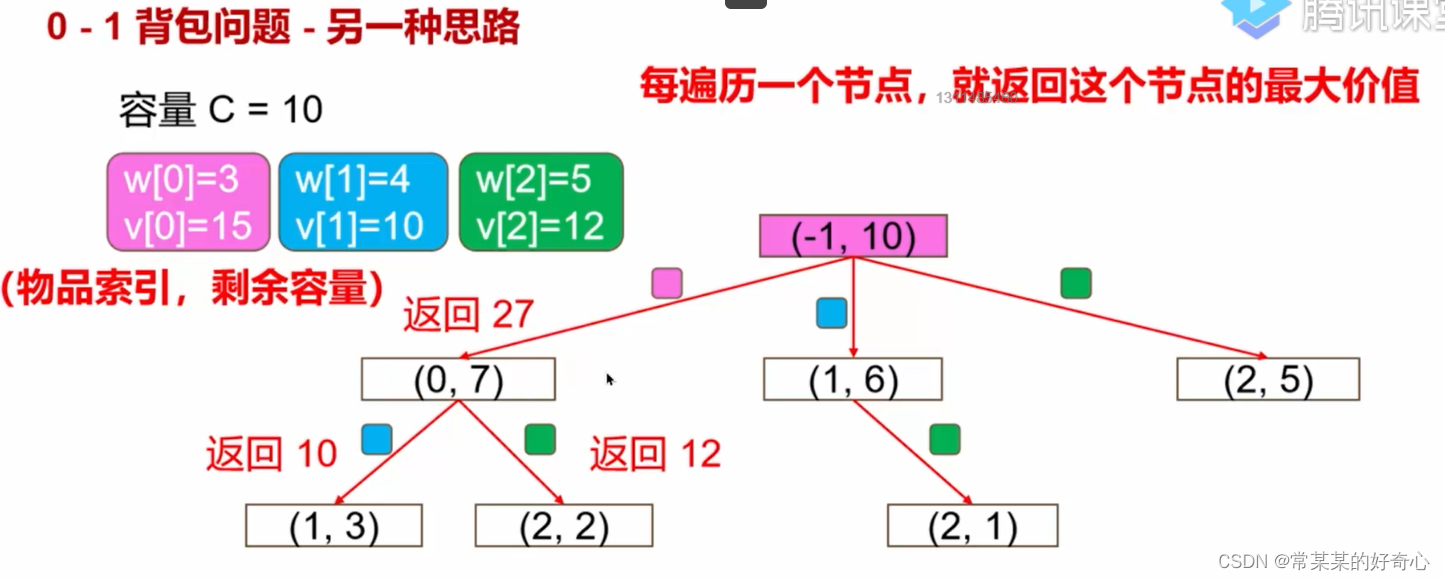
#方案二:dfs-后序
def knapsack01(w, v, C):
def dfs(start,remain_w):
maxValue = 0 #key:位置,最底子节点maxValue从0开始
#
for i in range(start,len(w)):
child_i=i+1
if child_i==len(w):continue
if remain_w-w[child_i]<0:continue
#
childmaxValue=dfs(child_i, remain_w - w[child_i])
maxValue=max(maxValue,childmaxValue) #考虑到,返回各子分支中的最大值
k=0 if start==-1 else v[start]
return maxValue+k
return dfs(-1, C)
print(knapsack01([3,6,7],[15,10,11],10))
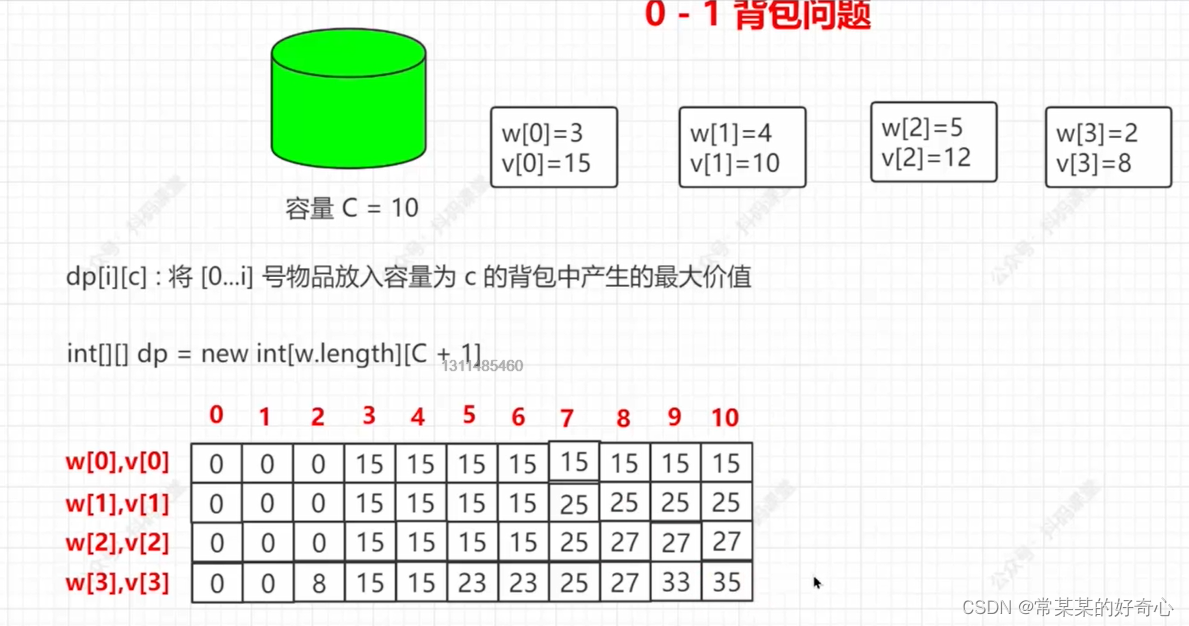
#方案三:dp
def knapsack01(w, v, c):
dp=[[0]*(c+1) for _ in range(len(w))]
for j in range(c+1):
if j>=w[0]:dp[0][j]=v[0]
for i in range(1,len(w)):
for j in range(c+1):
if j<w[i]:dp[i][j]=dp[i-1][j]
else:dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]])
return dp[len(w)-1][c]
print(knapsack01([3,6,7],[15,14,13],10))
#方案四:dp+状态压缩(注意状态转移方向)【重】
def knapsack01(w, v, c):
dp=[0]*(c+1)
#for j in range(c+1): #可以被下面统一化
#if j>=w[0]:dp[j]=v[0] #dp[j]=max(0,v[i]+0)
for i in range(len(w)):#1->0
for j in range(w[i],-1,-1): #转移方向,使基于前面的状态没有被提前改变
dp[j]=max(dp[j],v[i]+dp[j-w[i]])
return dp[c]
print(knapsack01([3,6,7],[15,14,13],10))
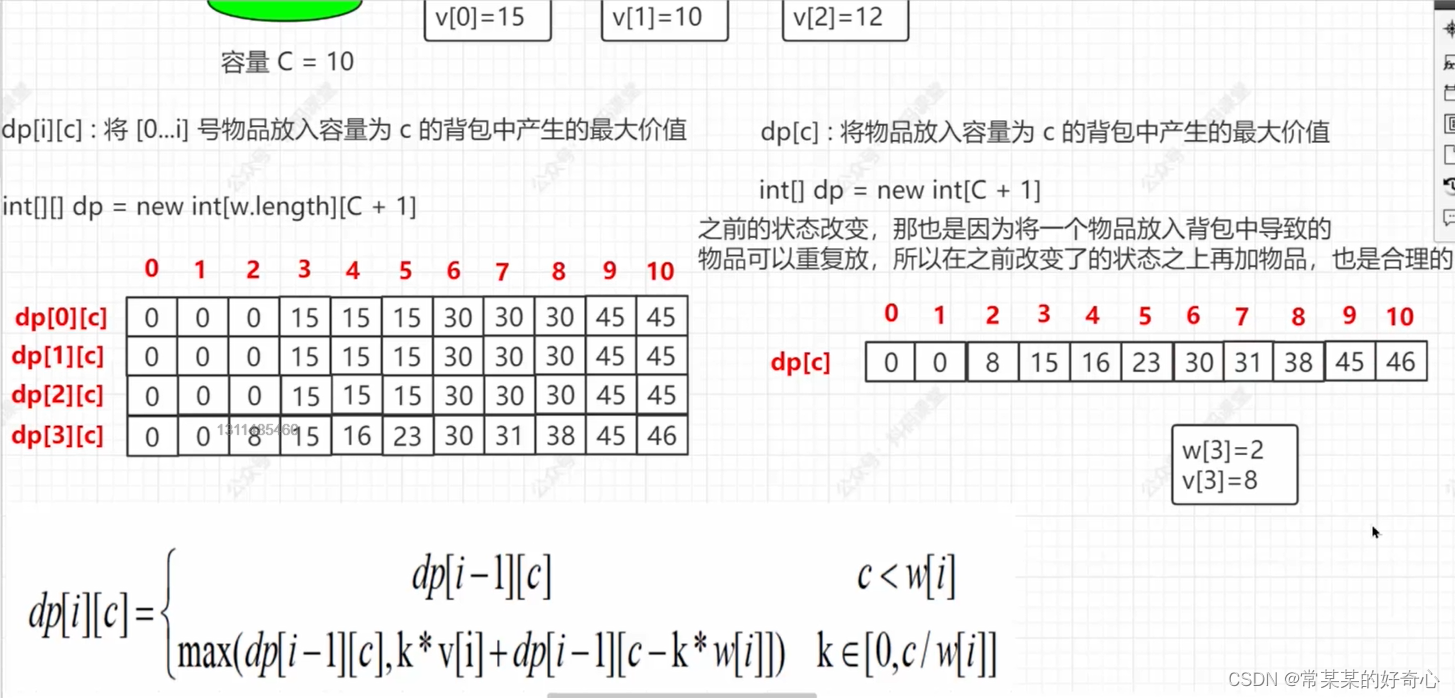
完全背包问题:每种背包可以重复取
#dfs
def knapsackComplete(w, v, c):
def dfs(start,remain_w):
maxValue=0
#处理子节点
for i in range(start,len(w)):
child_i=i
#剪枝
if child_i==-1 or child_i==len(w):continue
if remain_w-w[child_i]<0:continue
maxValue=max(maxValue,dfs(child_i,remain_w-w[child_i]))
k=0 if start==-1 else v[start]
return maxValue + k
return dfs(-1, c)
print(knapsackComplete([3,6,7],[16,14,13],10))
#dp
def knapsackComplete(w, v, c):
dp = [[0] * (c + 1) for _ in range(len(w))]
for j in range(c + 1):
dp[0][j] = (j//w[0])*v[0]
for i in range(1, len(w)):
for j in range(c + 1):
max_cnt=j//w[i]
for k in range(max_cnt+1):
dp[i][j] = max(dp[i][j], k*v[i] + dp[i - 1][j - k*w[i]]) #key
return dp[len(w) - 1][c]
print(knapsackComplete([3,3,7],[18,17,13],10))
#dp+时空优化【重】
def knapsackComplete(w, v, c):
dp = [0] * (c + 1) #空间优化
#for j in range(c + 1):
#dp[j] = (j//w[0])*v[0]
for i in range(len(w)):
for j in range(w[i],c + 1):
#放 第一个物品产生的价值永远大于等于放 第 2、3、4、5.... 个
#如果放第一个物品产生的价值比不放这个物品产生的价值要小的话,那么不放物品,产生的价值最大
dp[j]=max(dp[j],v[i]+dp[j-w[i]]) #时间优化 #key:#转移方向:使基于前面的状态被提前改变
# max_cnt=j//w[i]
# for k in range(max_cnt+1):
# dp[j] = max(dp[j], k*v[i] + dp[j - k*w[i]]) #key
return dp[c]
print(knapsackComplete([3,3,7],[18,17,13],10))
#多重背包
def knapsackM(w, v, c, p):
dp = [0] * (c + 1) #空间优化
for i in range(len(w)):
for j in range(c,w[i]-1,-1):#key:非重复选(<=p[i])
max_cnt=min(j//w[i],p[i])
for k in range(max_cnt+1):
dp[j] = max(dp[j], k*v[i] + dp[j - k*w[i]]) #key
return dp[c]
print(knapsackM([3,3,7],[18,17,13],10,[2,2,0]))
#二维背包
def knapsackComplete(w,g,W,G,v):#两种代价
dp = [[0] * (G+1) for _ in range(W+1)] #空间优化
for i in range(len(w)):
for j in range(W,w[i]-1,-1):
for k in range(G,g[i]-1,-1):
dp[j][k] = max(dp[j][k], v[i] + dp[j-w[i]][k-g[i]]) #key
return dp[w][G]

lc 322【剑指 103】:零钱兑换
https://leetcode.cn/problems/coin-change/
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp=[float('inf')]*(amount+1)
dp[0]=0 #key-遗漏
for i in range(len(coins)):
for j in range(coins[i],amount+1):
dp[j]=min(dp[j],1+dp[j-coins[i]])
return dp[amount] if dp[amount]!=float('inf') else -1
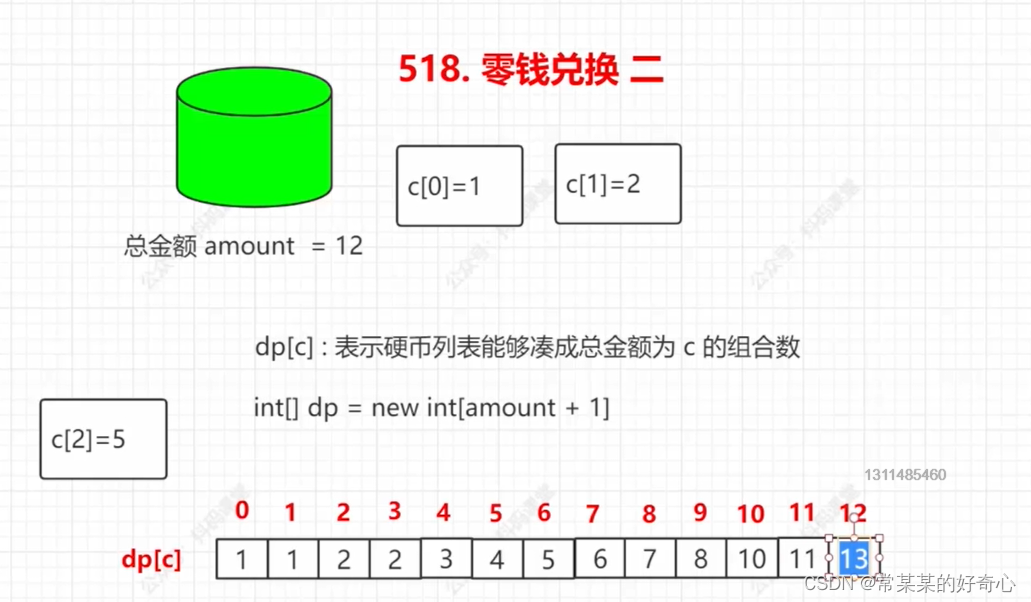
lc 518 :零钱兑换 II
https://leetcode.cn/problems/coin-change-ii/
提示:
1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp=[0]*(amount+1)
dp[0]=1 #key:例如dp[5]=dp[5]+dp[0],5凑5本身就是一种组合
for i in range(len(coins)):
for j in range(coins[i],amount+1):
dp[j]=dp[j]+dp[j-coins[i]] #上一个状态中,本身的组合数+新coins[i]带来的新状态中,能得到的组合数
return dp[amount]
lc 377【剑指 104】 :组合总和 Ⅳ
https://leetcode.cn/problems/combination-sum-iv/
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 1000
nums 中的所有元素 互不相同
1 <= target <= 1000
进阶:
如果给定的数组中含有负数会发生什么?问题会产生何种变化?如果允许负数出现,需要向题目中添加哪些限制条件?
#请注意,顺序不同的序列被视作不同的组合。
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp=[0]*(target+1)
dp[0]=1
for j in range(1,target+1): #key:for顺序
for i in range(len(nums)):
if j>=nums[i]:
dp[j]=dp[j]+dp[j-nums[i]]
return dp[target]
lc 494【剑指 102】【top100】:目标和
https://leetcode.cn/problems/target-sum/
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
# 假设数组中所有数字的总和为 sum
# 假设前面设置为负数的数字的总和是 neg。那么设置为正数的数字的总和为 sum - neg
# 那么 (sum - neg) - neg = target => neg = (sum - target)/ 2
# 所以问题转为 0-1 背包问题:
# 在数组 nums 列表中不可重复的选择数字组合,使得组合中所有数字之和为 neg
# 求有多少组合数?
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
diff=sum(nums)-target
if diff%2==1 or diff<0:return 0 #key:sum(nums)>=0,target<=sum(nums)
#
neg=diff//2
dp=[0]*(neg+1)
dp[0]=1 #遗忘
for i in range(len(nums)):
for j in range(neg,nums[i]-1,-1):
dp[j]=dp[j]+dp[j-nums[i]]
return dp[neg]
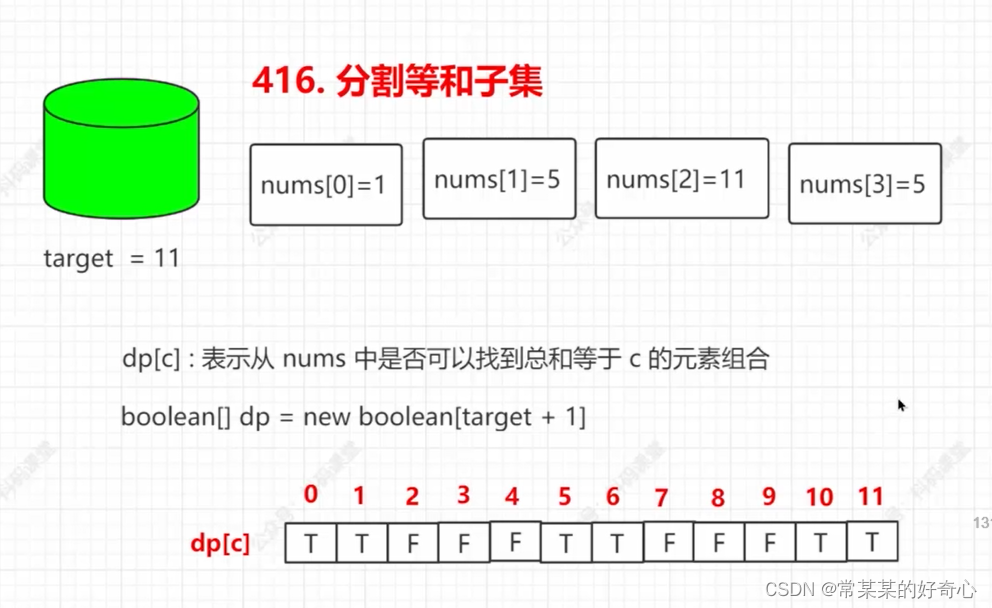
lc 416 【剑指 101】【top100】:分割等和子集
https://leetcode.cn/problems/partition-equal-subset-sum/
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
class Solution:
def canPartition(self, nums: List[int]) -> bool:
if sum(nums)%2==1:return False
target=sum(nums)//2
#
dp=[False]*(target+1)
dp[0]=True #遗忘
for i in range(len(nums)):
for j in range(target,nums[i]-1,-1):
dp[j]=dp[j] or dp[j-nums[i]]
return dp[target]
lc 279 :完全平方数【top100】
https://leetcode.cn/problems/perfect-squares/
提示:
1 <= n <= 10^4
# 完全平方数最小为 1,最大为 sqrt(n)
# 也就是我们要从 nums = [1, 2, ..., sqrt(n)] 数组里选出几个数,令其平方和为 target = n。
# 转化为是否可以用 nums 中的数(可重复选用)组合和成 n
class Solution:
def numSquares(self, n: int) -> int:
dp=[float('inf')]*(n+1)
dp[0]=0
for i in range(1,int(math.sqrt(n))+1):
for j in range(i**2,n+1):
dp[j]=min(dp[j],dp[j-i**2]+1)
return dp[n]
lc 474 :一和零
https://leetcode.cn/problems/ones-and-zeroes/
提示:
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100
# 二维费用背包问题
# 物品是字符串数组中的字符串,选择每个字符串有两个代价,分别是 0 的个数和 1 的个数
# 两个代价都有最大值,0 的个数最多为 m,1 的个数最多为 n
# 求选择字符串得到的最大子集的大小
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp=[[0]*(n+1) for _ in range(m+1)]
for i in range(len(strs)):
cnt=self.cntzeroone(strs[i])
for j in range(m,cnt[0]-1,-1): #cnt[0]->w[j],cnt[1]->v[k]
for k in range(n,cnt[1]-1,-1):
dp[j][k]=max(dp[j][k],dp[j-cnt[0]][k-cnt[1]]+1)
return dp[m][n]
def cntzeroone(self,s):
cnt=[0]*2
for i in range(len(s)):
cnt[ord(s[i])-ord('0')]+=1
return cnt
lc 139【top100】:单词拆分
https://leetcode.cn/problems/word-break/
注意:
不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅有小写英文字母组成
wordDict 中的所有字符串 互不相同
# 在 wordDict 中可重复的选择字符串组合,看看是否存在可以组成字符串 s
# dp[i]: 表示前 i 个字符组成的子串是否可以被 wordDict 中的字符串组合而成
# 注意:这里的组合的顺序是任意的,所以先选择字符,再选择每个字典字符串
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp=[False]*(len(s)+1)
dp[0]=True
for i in range(1,len(s)+1):
for word in wordDict:
if i>=len(word) and s[i-len(word):i]==word:#key:状态转移
dp[i]=dp[i] or dp[i-len(word)]
return dp[len(s)]
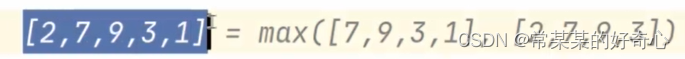

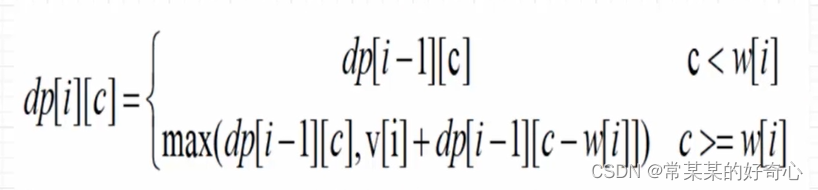






![[JavaEE]定时器](https://img-blog.csdnimg.cn/3e689866c9b9496196484c48de5f750e.png)