排序分为比较排序和非比较排序两种,常见的排序为比较排序,共有七类:直接插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序以及归并排序。另有三种非基于比较类的排序:计数排序、基数排序和桶排序。
基于比较的排序
直接插入排序
直接插入排序指的是按照顺序插入已排好的序列。就好比扑克牌,当摸到第二张牌时,如果牌大就放到第一张牌的右边,牌小就放在左边,每张牌这样处理,在摸完牌后,手中的扑克牌自然就有序了。
public static void insertSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for (; j >= 0; j--) {
if (array[j] > tmp) {
array[j + 1] = array[j];
}else {
break;
}
}
array[j + 1] = tmp;
}
}时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
当一组数据趋于有序时,直接插入排序就越快,如果一组数据是有序的(非逆序),则只需遍历一遍数据,时间复杂度为O(N)。特点是越有序越快。
希尔排序
希尔排序本质上是直接插入排序的优化,当数据较多时,直接插入排序效率很低,考虑把数据分组,局部有序之后再直接插入排序,从而提高效率。
具体实现为:两两有序成一组 -> 两组两组有序 -> 整体有序
尽量选择相距较远的两数为一组,尽可能保证大数和小数分开。例如:
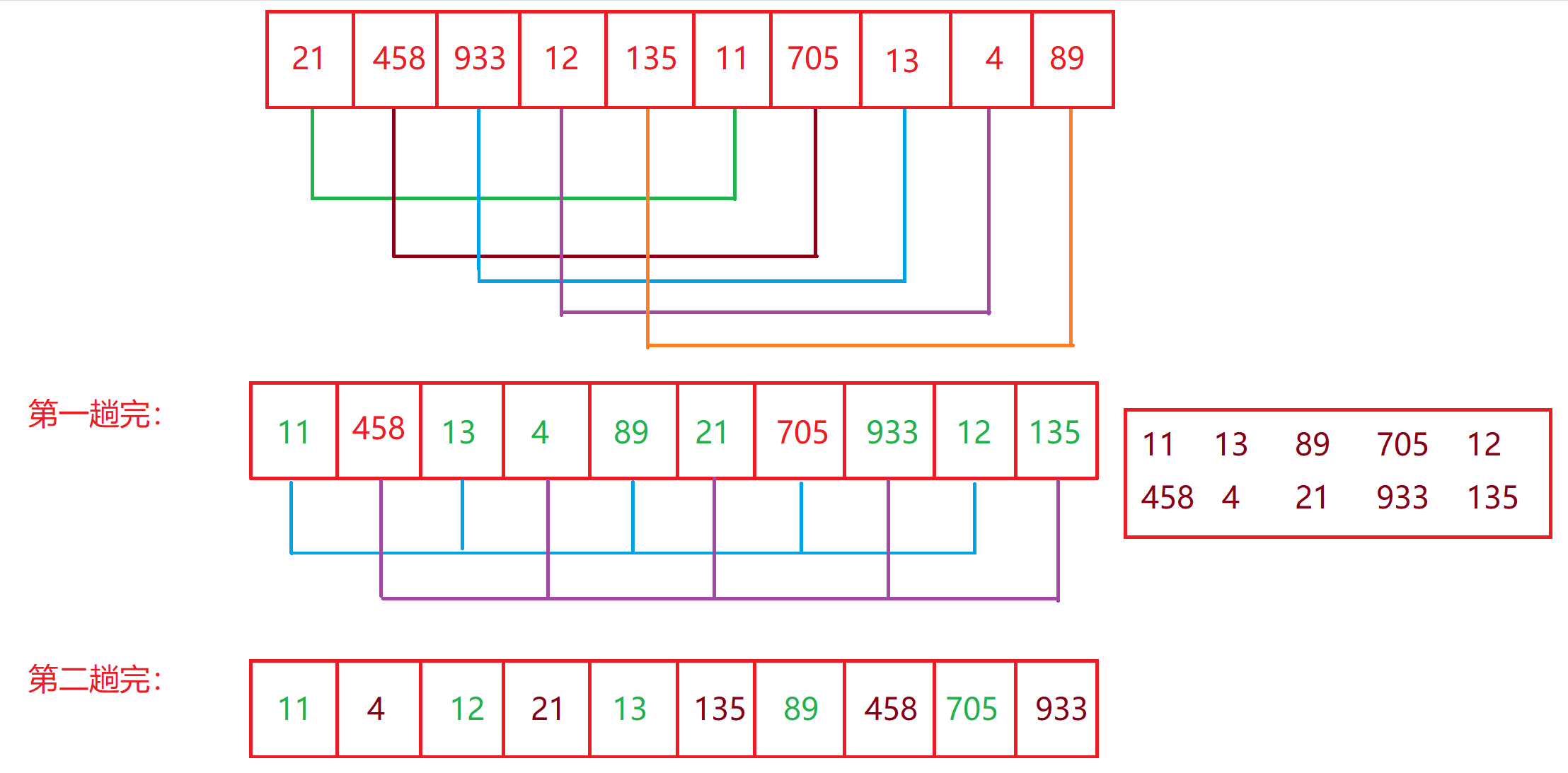
可以发现两次之后数据基本有序,这时在考虑直接插入排序效率较高:
public static void shellSort(int[] array) {
int gap = array.length;
while (gap > 1) {
shell(array, gap);
gap /= 2;
}
shell(array, 1);
}
private static void shell(int[] array, int gap) {
for (int i = 0; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
while (j >= 0) {
if (array[j] > tmp) {
array[j + gap] = array[j];
}else {
break;
}
j -= gap;
}
array[j + gap] = tmp;
}
}时间复杂度:大约在O(N^1.3) ~ O(N^1.6)之间,无法得出具体值
空间复杂度:O(1)
稳定性:不稳定
选择排序
选择排序的基本思路:遍历数组找到最小的值(或最大)与下标为0的元素交换,接着从下标为1的位置开始遍历找到最小的值(或最大)与下标为1的元素进行交换,依次遍历直到有序。
public static void selectSort(int[] array){
// write code here
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array, i, minIndex);
}
}
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}时间复杂度:O(N^2) ->任何情况下时间复杂度不变
空间复杂度:O(1)
稳定性:不稳定
冒泡排序
思路:相邻两元素进行比较,值较大的(或较小)往后放,一轮遍历后最大值(或最小值)移到最右边
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length- 1 - i; j++) {
if (array[j + 1] < array[j]) {
swap(array, j + 1, j);
}
}
}
}
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
冒泡排序与选择排序均为思路简单但效率较低的排序算法,不过冒泡排序可以进行一定程度的优化,使其在处理有序的数组时效率更高:当一轮比较结束后,没有发生交换,就代表该序列有序,可以直接结束。但即使优化,也仅仅优化了有序的情况。
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length; i++) {
boolean flag = false;
for (int j = 0; j < array.length- 1 - i ; j++) {
if (array[j + 1] < array[j]) {
swap(array, j + 1, j);
flag = true;//代表未排完
}
}
if (!flag) return;
}
}堆排序
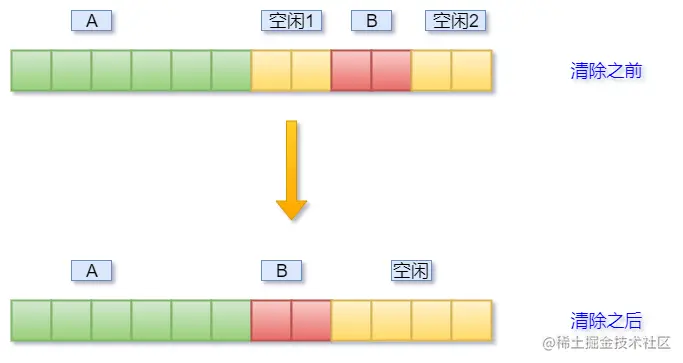
假如排升序,可以建立大根堆,每次把堆顶元素同末尾元素交换,同时堆的usedSize--(代表删除),向下调整成大根堆后重复操作,直到usedSize为0,此时堆有序。
例如:将序列[21,11,4,12,22,35,58,89,33]调整为升序序列:
首先建立大根堆:
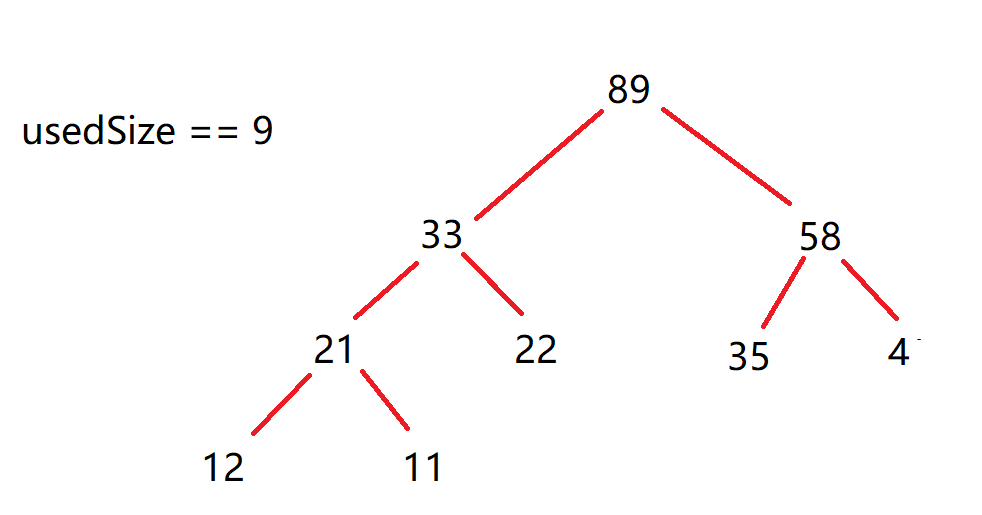
接着进行删除操作:
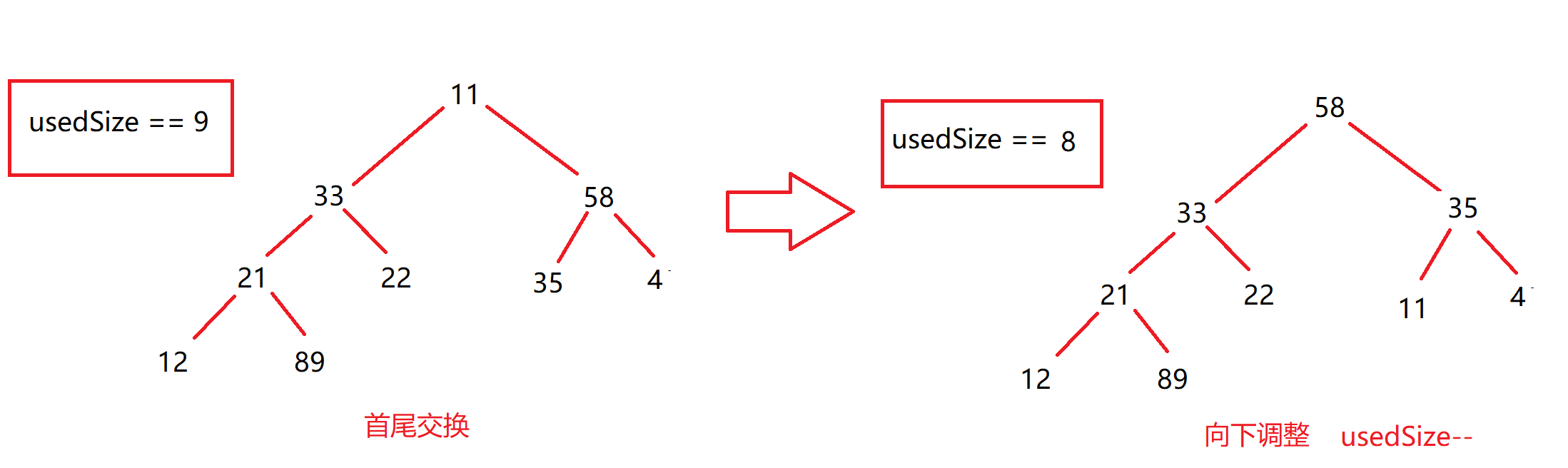
这样最大的“89”就有序了,依次进行交换和删除,最终序列有序。
可以自己模拟建堆并实现相关方法,或者直接使用PriorityQueue类也可行,PriorityQueue默认建小根堆,可以在建堆时添加构造器作为参数构建大根堆:
public static void heapSortB(int[] array) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((o1, o2) -> {
return o2.compareTo(o1);
});
for (int elem: array) {
priorityQueue.offer(elem);
}
for (int i = array.length - 1; i >= 0; i--) {
array[i] = priorityQueue.poll();
}
}new PriorityQueue<>()括号中为构造器。
时间复杂度:O(NlogN)
空间复杂度:O(1)
稳定性:不稳定
快速排序
快排属于一种二叉树式的排序,首先在待排序序列中找到某一元素作为基准值,把序列中小于基准值的放到基准值的左边,大于基准值的放到基准值的右边,这样基准值的位置是有序的。再分别出列基准值左边和右边的序列,直到整个序列有序,大体思路如下:
public static void quickSort(int[] array){
quickSortChild(array, 0, array.length - 1);
}
private static void quickSortChild(int[] array, int left, int right) {
//倘若基准值恰好是最小值,那么基准值下标为0,再去递归左边的序列会导致left = 0, right = -1
//因此left是有可能大于right的,右边同理,该情况下直接返回。
if (left >= right) return;
int pivot = partition(array, left, right);
quickSortChild(array, left, pivot - 1);
quickSortChild(array, pivot + 1, right);
}接下来就只需以基准值进行划分即可,常见方法有:Hoare法、挖坑法和前后指针法。
Hoare法:
private static int partition(int[] array, int left, int right) {
int tmp = left;//以首元素为基准值
while (left < right) {
while (left < right && array[right] >= array[tmp]) {
right--;//从后往前走,直到元素值小于基准值
}
while (left < right && array[left] <= array[tmp]) {
left++;//从前往后走,直到元素值大于基准值
}
swap(array, left, right);
}
//此时左右指针相遇,再与基准值交换
swap(array, tmp, left);
return left;
}注意一定要先走右边,先走右边可以保证相遇时左右指针指向的值一定小于基准值,若先走左,则停下时必定停在大于基准值的位置,再交换该值与基准值必然破坏序列的有序性。
挖坑法:
private static int partition1(int[] array, int left, int right) {
int pivot = array[left];
while (left < right) {
while (left < right && array[right] >= pivot) {
right--;
}
array[left] = array[right];
while (left < right && array[left] <= pivot) {
left++;
}
array[right] = array[left];
}
array[left] = pivot;
return left;
}逻辑上大体相似,依然是先走右边,找到时直接将right指向的值赋给left即可(每次right走的时候,left指向的值均是无用值,因此可以直接覆盖,left走时同理),左右相遇的位置就是基准值应在的位置。
前后指针法:
private static int partition2(int[] array, int left, int right) {
int prev = left;
int cur = left + 1;
while (cur <= right) {
if (array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array, prev, cur);
}
cur++;
}
swap(array, prev, left);
return prev;
}当cur指向的值大于基准值时,cur向前走,当小于基准值时cur和prev都向前走,这样在cur小于基准值时,prev的下一个值必定大于基准值。
时间复杂度:O(NlogN)
空间复杂度:O(logN)
稳定性:不稳定
当一组数据完全有序时,时间复杂度为O(N^2),空间复杂度为O(N)。考虑有序的情况,可以进行一定程度的优化:在选取基准值前,可以先确定首元素中间元素和尾元素中中间大小的值与首元素交换,避免完全有序的情况。也可以在数据较少时,选择其他排序方法,例如直接插入排序(此时占用的空间非常多),这样可以避免当数据量非常庞大时造成栈溢出的情况。
非递归快速排序:
利用栈的先进后出特性将序列的首尾元素入栈,需要排序时出栈即可:
public static void quickSortNor(int[] array) {
Deque<Integer> stack = new ArrayDeque<>();
int left = 0;
int right = array.length - 1;
stack.push(left);
stack.push(right);
while (!stack.isEmpty()) {
//先入的是left,所以后出的是left
right = stack.pop();
left = stack.pop();
if (right - left < 1) {
continue;//代表该段序列最多有一个元素,不用排序
}
int pivot = partition(array, left, right);
//把左边序列的left和right入栈
stack.push(left);
stack.push(pivot);
//把右边序列的left和right入栈
stack.push(pivot + 1);
stack.push(right);
}
}归并排序
归并排序:每次把待排序列均分成两个子序列,两个子序列有序后再进行合并。
大体框架如下:
public static void mergeSort(int[] array){
mergeSortChild(array, 0, array.length - 1);
}
private static void mergeSortChild(int[] array, int left, int right) {
if (left >= right) return;//此处原因同快排
int mid = (right + left) / 2;
mergeSortChild(array, left, mid);
mergeSortChild(array, mid + 1, right);
merge(array, left, right, mid);//这里的right - left是两个序列的总长度
}框架也可以由非递归实现:
public static void mergeSortNor(int[] array){
int gap = 1;//gap代表需要合并的两个序列的各自长度
while (gap < array.length) {
for (int i = 0; i < array.length; i += 2 * gap) {
//合并一组
int mid = i + gap - 1;//可能越界
if (mid >= array.length) {
mid = array.length - 1;
}
int j = mid + gap;
if (j >= array.length) {
j = array.length - 1;
}
merge(array, i, j, mid);
}
gap *= 2;
}
}那么实现这个排序地关键就是合并两个序列:
两个有序序列的合并:[9, 53, 73, 82]和[3, 7, 20, 45]
一定是首元素比较,小的放进来,往后走,再比较,直到一方走完。此时未走完的序列中所有的值一定是有序的且都大于已放入的元素,因此只需把剩余元素依次拷贝进来即可:
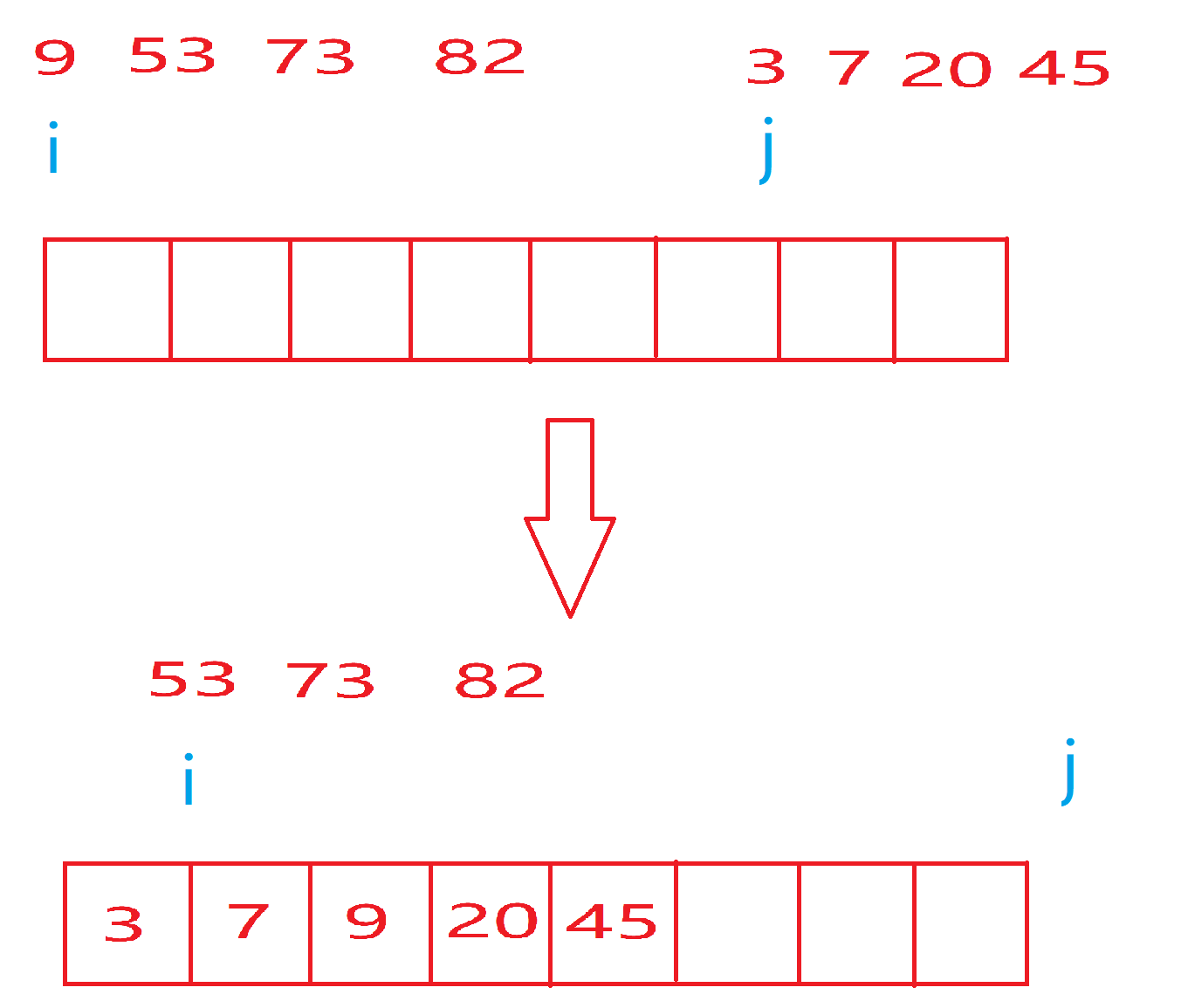
private static void merge(int[] array, int left, int right, int mid) {
int s1 = left, s2 = mid + 1;
int[] tmp = new int[right - left + 1];
int i = 0;
//s1-mid为第一段序列,mid + 1-right为第二段序列
while (s1 <= mid && s2 <= right) {
if (array[s1] < array[s2]) {
tmp[i++] = array[s1++];
}else {
tmp[i++] = array[s2++];
}
}
//剩余序列依次放入
while (s1 <= mid) {
tmp[i++] = array[s1++];
}
while (s2 <= right) {
tmp[i++] = array[s2++];
}
//注意拷贝到原数组时数组下标+left才是原数组的真正下标
//比如left为5,那么tmp[0]的值就要放到array[0 + 5]
System.arraycopy(tmp, 0, array, left, tmp.length);
}时间复杂度:O(NlogN)
空间复杂度:O(N)
稳定性:稳定
归并排序属于稳定排序,归并排序常用来处理海量数据的排序问题,归并排序的排序效率略低于快速排序
非基于比较的排序
基于比较的排序速度最快的时间复杂度也有O(NlogN),若要实现时间复杂度为线性,则需要考虑以空间换时间的做法,即计数排序、基数排序和桶排序。
计数排序
首先确定最大值和最小值,创建一个长度为最大值-最小值+1的计数数组,遍历到某个元素就在计数数组的相应下标所指的值+1,遍历完再根据计数数组返回原数组。
一种简单写法:该写法不稳定
public static void countSort(int[] array){
int min = array[0];
int max = array[0];
for (int elem : array) {
if (elem < min) {
min = elem;
} else if (elem > max) {
max = elem;
}
}
int[] tmp = new int[max - min + 1];
for (int elem : array) {
tmp[elem - min]++;
}
for (int i = 0, j = 0; i < tmp.length; i++) {
if (tmp[i] >= 1) {
array[j++] = i + min;
tmp[i--]--;
}
}
}若要实现稳定排序,需要再额外创建一个数组来存放从计数数组中返回的值,最后再复制到原数组:
public static void countSortB(int[] array) {
int min = array[0];
int max = array[0];
for (int elem : array) {
if (elem < min) {
min = elem;
} else if (elem > max) {
max = elem;
}
}
int[] tmp = new int[max - min + 1];
int[] ret = new int[array.length];
for (int elem : array) {
tmp[elem - min]++;
}
for (int i = 1; i < tmp.length; i++) {
tmp[i] += tmp[i - 1];//tmp[i] 表示比i + min小的数有tmp[i] - 1个
}
for (int i = array.length - 1; i >= 0; i--) {
//这里的array[i] - min == 上一个for循环中的i
ret[--tmp[array[i] - min]] = array[i];//前面有几个就放在下标是几的位置
//从后往前,先出现的放在后面,从而稳定
}
System.arraycopy(ret, 0, array, 0, array.length);
}时间复杂度:O(N) 实际上是N + max - min
空间复杂度:O(N) 实际上是N + max - min
稳定性:稳定
计数排序速度很快,但占用空间较多,当数据较为集中时,可以考虑计数排序。
桶排序
桶排序实际上是基于计数排序的一种变形:它不再是一个值放在一个位置,而是某个范围内的值放到某块空间,在每块空间内分别排序,直到每个空间都有序,按顺序返回原数组即有序:
比如说0~50的数据,可以分为5个桶0~9放到桶1中,10~19放到桶2中,20~29放到桶3中,30~39放到桶4中,40~49放到桶5中,还剩一个最大值50,放到桶5中。接着排序,返回。
public static void bucketSort(int[] array) {
int max = array[0];
int min = array[0];
for (int elem : array) {
if (elem > max) {
max = elem;
} else if (elem < min) {
min = elem;
}
}
//(max - min) / array.length仅为一种计算桶数量的方式,可以任意指定
int bucketNum = (max - min) / array.length + 1;//+1保证最大值也能入桶
ArrayList<ArrayList<Integer>> buckets = new ArrayList<>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
buckets.add(new ArrayList<>());//创建桶
}
for (int elem : array) {
int num = (elem - min) / array.length;//这里要保持和bucketNum一致
buckets.get(num).add(elem);//在相应桶中添加元素
}
for (ArrayList<Integer> bucket : buckets) {
Collections.sort(bucket);//每个桶内元素进行排序,也可以用其他排序方法
}
for (int i = 0, k = 0; i < buckets.size(); i++) {
for (int j = 0; j < buckets.get(i).size(); j++) {
array[k++] = buckets.get(i).get(j);
}
}
}时间复杂度:O(N)->假如有M个桶,三次遍历整个数组为O(3 * N) + 一次遍历M个桶,桶内排序一般采用最快的算法为O(NlogN),则一个桶内的时间复杂度为:O(N/M * log(N/M)),M个桶时间复杂度为:O(N*(logN - logM)),整个过程时间复杂度为:O(N*(logN - logM + 3) + M)。当N = M时,化简后为O(N)
空间复杂度:O(N + M)
稳定性:稳定 ->桶内排序算法稳定即稳定
基数排序
基数排序是一种非常神奇的排序算法,首先需要创建10个数组(不考虑负数的话)用来存放数据,接着遍历数组,个位数为几就放进哪个数组,一轮遍历后按照顺序拿出来(先进先出),再按照新的顺序遍历,十位数为几就放进哪个数组,以此类推,直到最高位也处理完,数组就是有序的了:
例如对下列数据排序:[122, 245, 78, 4, 902, 34, 56, 44, 83, 32]

第一轮遍历
按顺序拿出来为[122, 902, 32, 83, 4, 34, 44, 245, 56, 78],接着按十位放
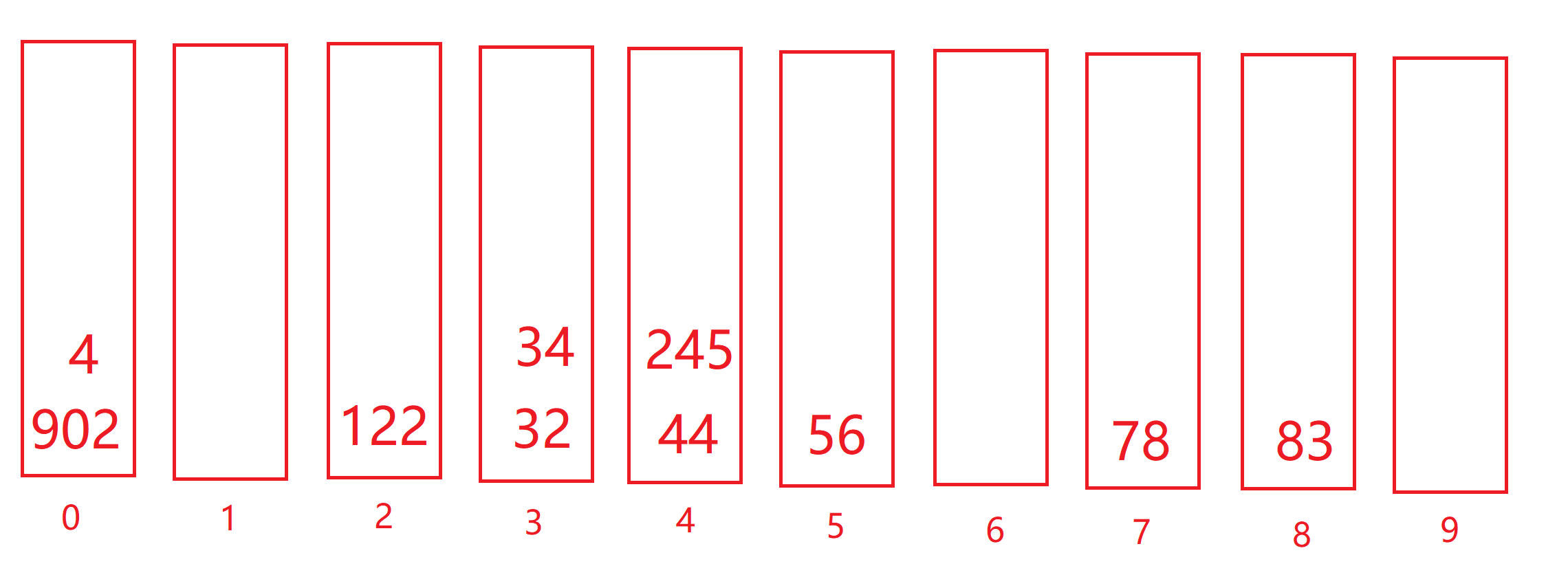
第二轮遍历
按顺序拿出来:[902, 4, 122, 32, 34, 44, 245, 56, 78, 83],再按百位放
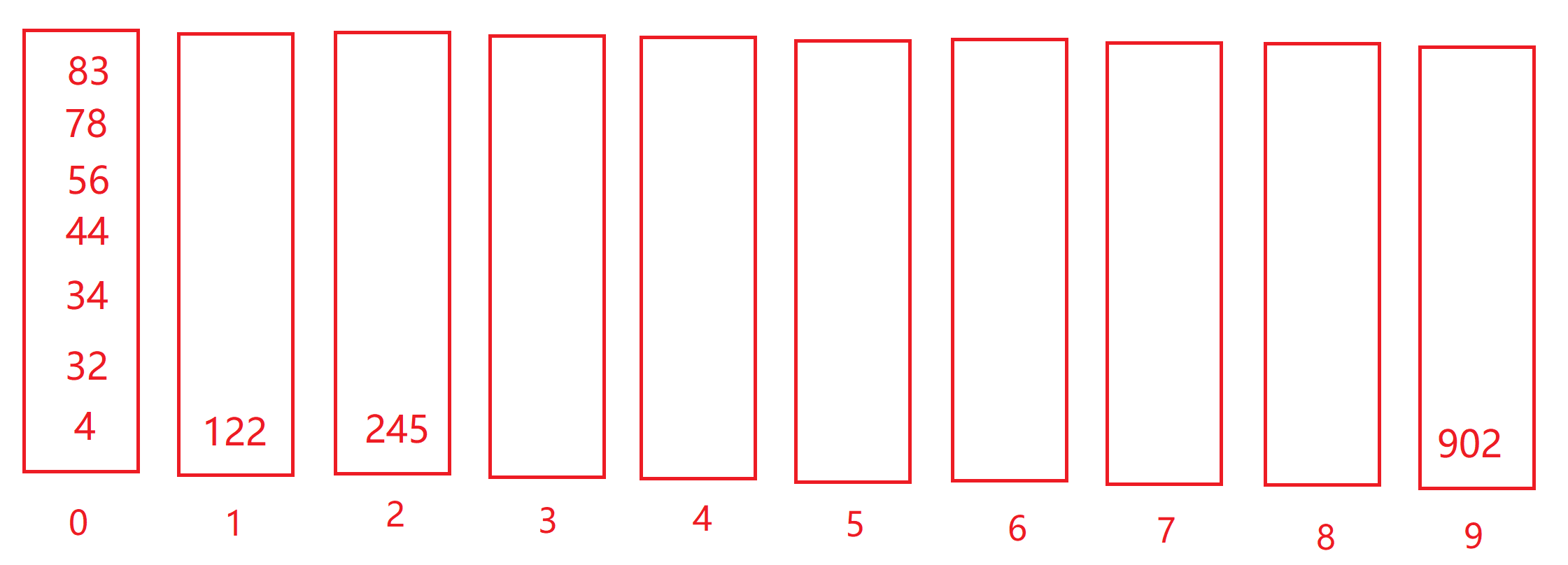
第三轮遍历
按顺序拿出来:[4, 32, 34, 44, 56, 78, 83, 122, 245, 902],可以看到已经有序。
public static void baseSort(int[] array) {
int[][] base = new int[10][array.length];
int[] count = new int[10];//存放目标位数值的个数
int maxDigit = getMaxDigit(array);//得到最大位数
int digit = 1;//当前需要的位数
while (maxDigit > 0) {
//往base数组存值
for (int value : array) {
int tmp = value / digit % 10;//目标元素目标位数上的值
base[tmp][count[tmp]++] = value;
}
//放好的值按顺序拿出来
for (int i = 0, k = 0; i < 10; i++) {
int j = 0;
while (count[i] > 0) {
array[k++] = base[i][j++];
count[i]--;
}
}
digit *= 10;
maxDigit--;
}
}
private static int getMaxDigit(int[] array) {
int max = array[0];
for (int elem : array) {
if (elem > max) {
max = elem;
}
}
int count = 0;
while (max > 0) {
count++;
max /= 10;
}
return count;
}当然,这样是不能处理负数的,为了把负数添加进来,可以创建二十个数组,前十个用来放负数,因此代码就改成:
public static void baseSort(int[] array) {
int[][] base = new int[20][array.length];
int[] count = new int[20];//存放目标位数值的个数
int maxDigit = getMaxDigit1(array);//得到最大位数
int negNum = getNegNum(array);//得到数组中的负数个数
int digit = 1;//当前需要的位数
while (maxDigit > 0) {
//往base数组存值
for (int value : array) {
if (value < 0) {
int tmp = -value / digit % 10;//目标元素目标位数上的值
base[tmp][count[tmp]++] = value;//0-9的位置存负数
}else {
int tmp = value / digit % 10;//目标元素目标位数上的值
base[tmp + 10][count[tmp + 10]++] = value;
}
}
//放好的值按顺序拿出来
int k = 0;
for (int i = 0; i < 20; i++) {
int j = 0;
while (count[i] > 0) {
array[k++] = base[i][j++];
count[i]--;
}
}
digit *= 10;
maxDigit--;
}
//负数的顺序是反的,需要交换顺序
for (int i = 0; i < negNum / 2; i++) {
swap(array, i, negNum - 1 - i);
}
}
//得到负数的个数
private static int getNegNum(int[] array) {
int count = 0;
for (int elem : array) {
if (elem < 0) {
count++;
}
}
return count;
}
private static int getMaxDigit1(int[] array) {
//负数也要考虑,因此要找到最大值和最小值
int max = array[0];
int min = array[0];
for (int elem : array) {
if (elem > max) {
max = elem;
}else if (elem < min) {
min = elem;
}
}
min = -min;
max = Math.max(max, min);
int count = 0;
while (max > 0) {
count++;
max /= 10;
}
return count;
}时间复杂度:O(N)
空间复杂度:O(N)
稳定性:稳定
该算法虽然较快,但消耗的空间较多,空间复杂度实际上是20 * N。






![[Arduino]环境安装与配置](https://img-blog.csdnimg.cn/d715d61fc5ae40639addebd10c8c6041.png)