目录
LeetCode55跳跃游戏
LeetCode45. 跳跃游戏 II
LeetCode1306. 跳跃游戏 III
LeetCode1345. 跳跃游戏 IV
LeetCode55跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
public boolean canJump(int[] nums) {
int k = 0;
for (int i = 0; i < nums.length; i++) {
//k追不上i就认为没法跳到最后一步
if (i > k) return false;
k = Math.max(k, i + nums[i]);
}
return true;
}LeetCode45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4] 输出: 2
public int jump(int[] nums) {
int length = nums.length;
//因为要统计步数所以引入边界值end
int end = 0;
int maxPosition = 0;
int steps = 0;
for (int i = 0; i < length - 1; i++) {
maxPosition = Math.max(maxPosition, i + nums[i]);
//跳到边界时用maxPosition更新边界end
//步数steps加1
if (i == end) {
end = maxPosition;
steps++;
}
}
return steps;
}LeetCode1306. 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5 输出:true 解释: 到达值为 0 的下标 3 有以下可能方案: 下标 5 -> 下标 4 -> 下标 1 -> 下标 3 下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0 输出:true 解释: 到达值为 0 的下标 3 有以下可能方案: 下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2 输出:false 解释:无法到达值为 0 的下标 1 处。
/**
* 广度优先,利用used减枝
**/
public boolean canReach(int[] arr, int start) {
if (arr[start] == 0) {
return true;
}
int n = arr.length;
//标记已经访问过的节点
Set<Integer> used = new HashSet<Integer>();
used.add(start);
LinkedList<Integer> deque = new LinkedList<>();
deque.add(start);
while (deque.size() > 0) {
Integer u = deque.poll();
ArrayList<Integer> list = new ArrayList<>();
list.add(u - arr[u]);
list.add(u + arr[u]);
for(Integer v: list) {
if (v >= 0 && v < n && !used.contains(v)) {
if (arr[v] == 0) {
return true;
}
deque.offer(v);
used.add(v);
}
}
}
return false;
}LeetCode1345. 跳跃游戏 IV
给你一个整数数组 arr ,你一开始在数组的第一个元素处(下标为 0)。
每一步,你可以从下标 i 跳到下标 i + 1 、i - 1 或者 j :
i + 1需满足:i + 1 < arr.lengthi - 1需满足:i - 1 >= 0j需满足:arr[i] == arr[j]且i != j
请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。
注意:任何时候你都不能跳到数组外面。
示例 1:
输入:arr = [100,-23,-23,404,100,23,23,23,3,404] 输出:3 解释:那你需要跳跃 3 次,下标依次为 0 --> 4 --> 3 --> 9 。下标 9 为数组的最后一个元素的下标。
示例 2:
输入:arr = [7] 输出:0 解释:一开始就在最后一个元素处,所以你不需要跳跃。
示例 3:
输入:arr = [7,6,9,6,9,6,9,7] 输出:1 解释:你可以直接从下标 0 处跳到下标 7 处,也就是数组的最后一个元素处。
提示:
1 <= arr.length <= 5 * 104-108 <= arr[i] <= 108
直接递归,再通过缓存减枝,结束循环会超时
class Solution {
//记录从下标0到index处所需的最少步数
private Map<Integer,Integer> indexCache = new HashMap<Integer,Integer>();
//key 数组值,value 数组下标
private Map<Integer,List> numberCache = new HashMap<Integer,List>();
private Integer minStep=Integer.MAX_VALUE;
public int minJumps(int[] arr) {
getNumberCache(arr);
minStep(0,0,arr);
return minStep;
}
private void getNumberCache(int[] arr){
for(int i=0;i<arr.length;i++){
List list = numberCache.get(arr[i]);
if(list!=null){
list.add(i);
}else{
list = new ArrayList();
list.add(i);
numberCache.put(arr[i],list);
}
}
}
private void minStep(int index,int step,int[] arr){
if(index==arr.length-1){
minStep = Math.min(minStep,step);
}
Integer last = indexCache.get(index);
if(last!=null){
//遇到更小的步数更新indexCache的值否则直接结束循环
if(step < last) {
indexCache.put(index,step);
}else {
return;
}
}else {
indexCache.put(index,step);
}
List<Integer> params = new ArrayList();
if(index-1 >= 0){
params.add(index-1);
}
if(index+1 < arr.length){
params.add(index+1);
}
List<Integer> list = numberCache.get(arr[index]);
for(int i=0;i<list.size() && list.size()>1;i++){
if(index!=list.get(i)){
params.add(list.get(i));
}
}
for(int i=0;i< params.size();i++){
minStep(params.get(i),step+1,arr);
}
}
}BFS的思路
根据题目描述,我们可以把给定数组整理成一个无向图,数组中相邻的元素或者元素值相同的元素相连即可。
比如,以示例1,给定的数组 arr = [100,-23,-23,404,100,23,23,23,3,404] 为例,转换成无向图为:
可以看到,我们只需要搜索下标从0到9的最短路径就可以了。
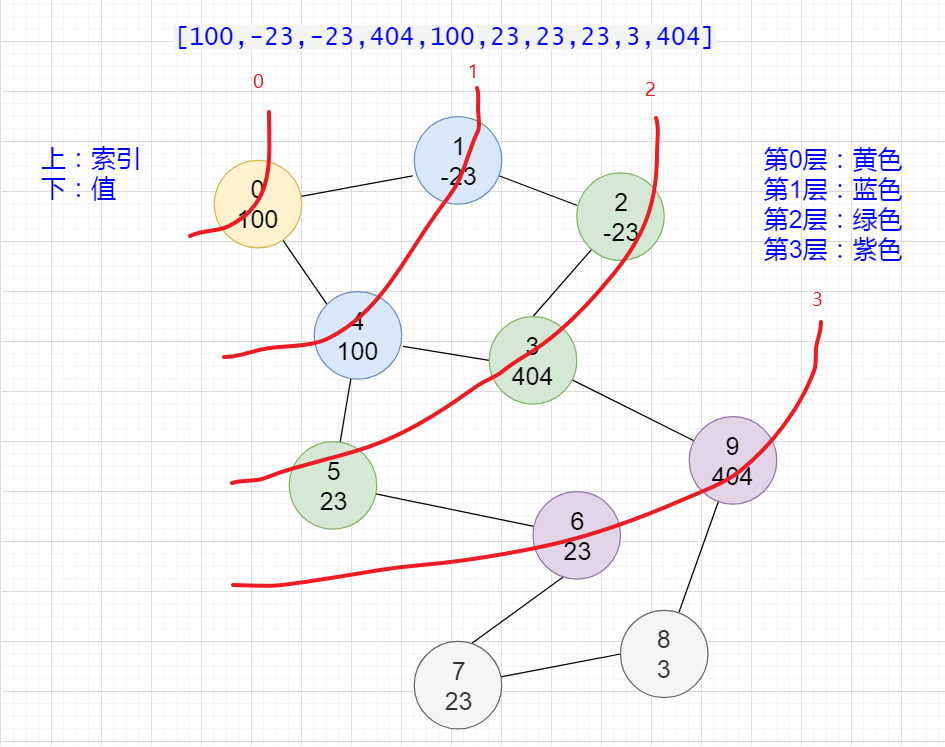
那当然是使用BFS了,图中,我也标记出来了遍历的过程,其实,就是类似于二叉树的层序遍历,BFS本身也是非常擅长最短路的查找的,只需要三层查找就可以找到9这个下标,所以,答案就是3。
理解了这个思路,再看代码就简单多了,我们先整理一下值相同的下标,使用 Map + List 来存储,然后就是BFS遍历,代码的书写方式跟二叉树的层序遍历的模板是一样的,区别是二叉树是有向图,而我们这里是无向图,所以,我们需要一个 visited 记录已经访问过的元素,防止重复访问。
另外,对于值相同的元素访问一次就够了,所以,还加入了一个剪枝的逻辑,只要map中的一个key遍历过,就把它移除防止重复遍历。
public int minJumps2(int[] arr) {
// 可以看成一张无向图,每个元素与它相邻的元素相连,同时还与它值相同的元素相连
// 使用BFS从0搜索到n-1即可
int n = arr.length;
if (n == 1) {
return 0;
}
// 记录相同值的元素有哪些下标
Map<Integer, List<Integer>> map = new HashMap<>();
for (int i = 0; i < n; i++) {
map.computeIfAbsent(arr[i], v -> new ArrayList<>()).add(i);
}
// BFS使用的队列
Queue<Integer> queue = new LinkedList<>();
// 记录已经访问过的元素
// 数组范围:1 <= arr.length <= 5 * 10^4
// 使用数组比Set效率更优
// 使用位图更优
boolean[] visited = new boolean[n];
queue.offer(0);
visited[0] = true;
int ans = 0;
while (!queue.isEmpty()) {
// 与二叉树的层序遍历类似
int size = queue.size();
while (size-- > 0) {
int index = queue.poll();
// 满足条件,直接返回
if (index == n - 1) {
return ans;
}
// 把它相边的直接入队
if (map.containsKey(arr[index])) {
for (int next : map.get(arr[index])) {
if (next != index && !visited[next]) {
queue.offer(next);
visited[next] = true;
}
// 剪枝:这个元素相连的都处理过了,后面再遍历到再处理肯定都已经访问过了,不如直接移除,可以减少遍历的次数
map.remove(arr[index]);
}
}
if (index + 1 <= n - 1 && !visited[index + 1]) {
queue.offer(index + 1);
visited[index + 1] = true;
}
if (index - 1 >= 0 && !visited[index - 1]) {
queue.offer(index - 1);
visited[index - 1] = true;
}
}
ans++;
}
// 不会走到这里
return -1;
}






![[Arduino]环境安装与配置](https://img-blog.csdnimg.cn/d715d61fc5ae40639addebd10c8c6041.png)