C++/C 线性插值

news2024/12/24 9:13:16

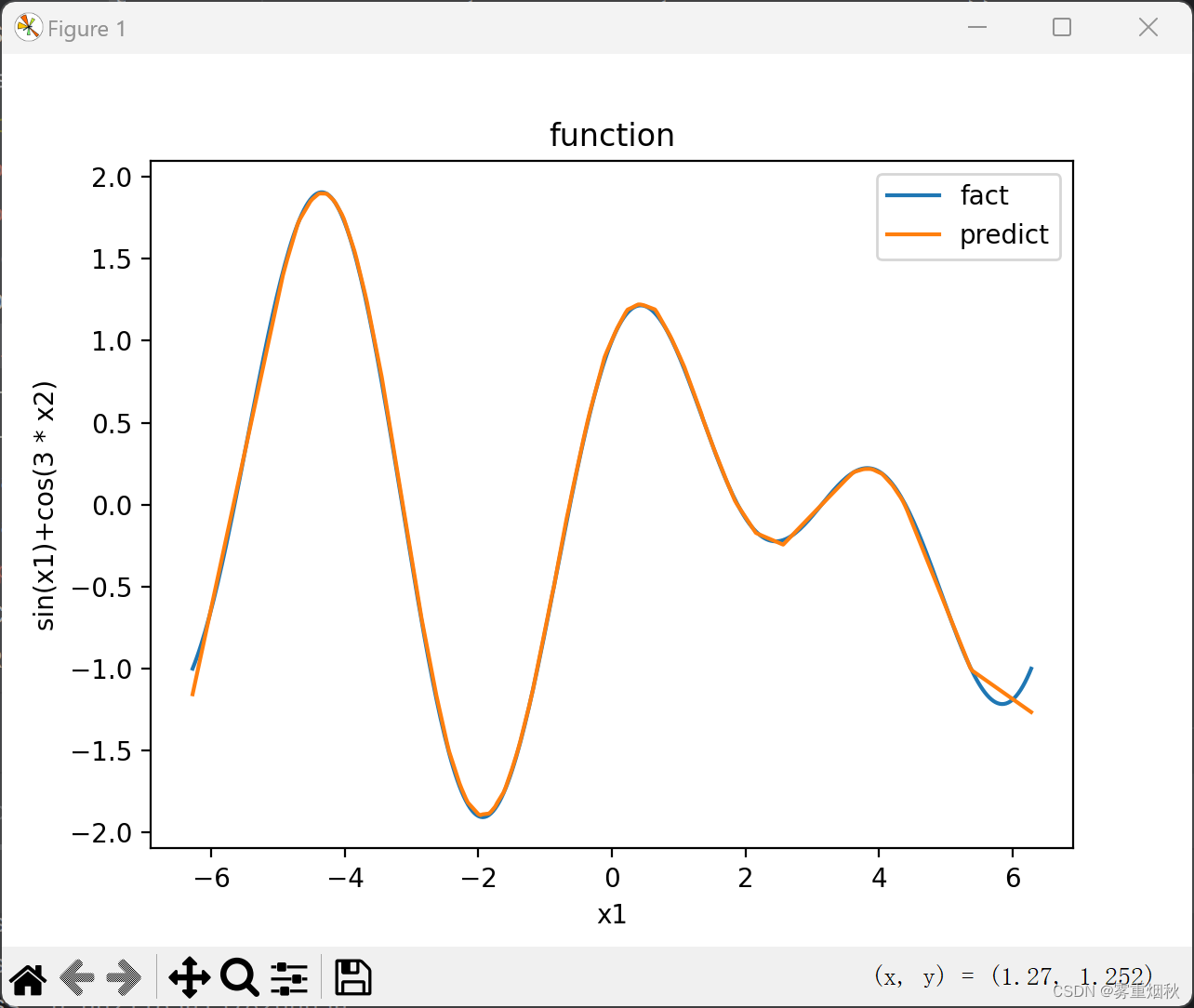
插值

插值，是根据已知的数据序列（可以理解为你坐标中一系列离散的点），找到其中的规律，然后根据找到的这个规律，来对其中尚未有数据记录的点

应用

对缺失的数据进行补偿
对图像进行放大缩小

通用公式

在这里插入图片描述
如上图，该公式为通用公式。可以看到，该公式为线性变化

常见的传统插值方法有

最邻近插值（0阶线性插值）

解释：取相邻最近的值。实际中可用四舍五入操作
这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近邻的像素灰度赋给待求象素。设为待求象素坐标(x+u,y+v) ，【注：x,y为整数， u，v为大于零小于1的小数】则待求象素灰度的值 f(x+u,y+v)为，选取距离插入的像素点（x+u, y+v)最近的一个像素点，用它的像素点的灰度值代替插入的像素点。

特点：最近邻插值法虽然计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

线性插值

解释：根据公式计算得出中间值，只有一个未知量。若两边界之差为最小单位时，则与最邻近插值一致
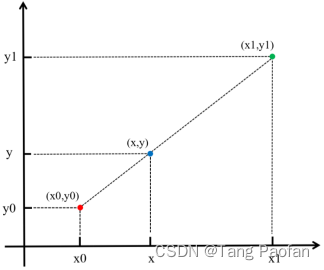
在这里插入图片描述
上图是一个一维线性插值的定量示意图，x0 和 x1 都是原有的坐标点，灰度值分别对应为 y0 和 y1。而灰度值未知的插值点 x，根据线性插值法约束，在 (x0, y0) 和 (x1, y1) 构成的一次函数上，其灰度值 y 即为

双线性插值

解释：双线性插值常见于二维平面，通过坐标关系，求解xy。核心思想是在两个方向上分别进行一次线性插值.
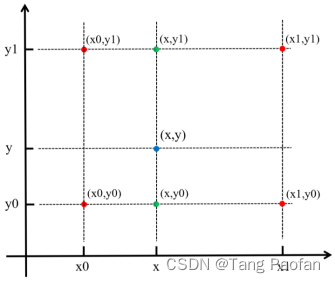
在这里插入图片描述
上图是一个二维双线性插值的定量俯视示意图 (点位稍有变动但不影响)，我们换个顺序。先由像素坐标点 (x0, y0) 和 (x1, y0) 在 x 轴向作一维线性插值得到 f(x, y0)、由像素坐标点 (x0, y1) 和 (x1, y1) 在 x 轴向作一维线性插值得到 f(x, y1)：
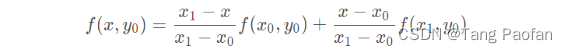
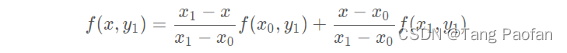
在这里插入图片描述

然后再由 (x, y0) 和 (x, y1) 在 y 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)：

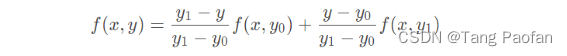
合并上式，得到最终的双线性插值结果：

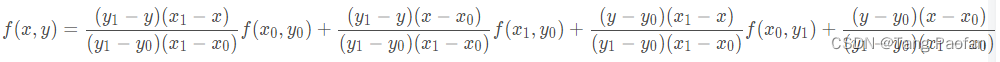
特点：双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点，结果基本令人满意。它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。

e.g.

// 二维图像缩放
void imagePixelProcess(BYTE* destData, int destW, int destH, BYTE* srcData, int srcW, int srcH, bool redFull, int* idList, int channel /*= 3*/)
{
	auto funcImageNearestScale = [destData, srcData, destW, srcW, channel](int destX, int destY, double scaleX, double scaleY) -> void
	{
		// NOTE 缩放，公式：destX * rx = srcW, destY * ry = srcH
		int srcX = std::round(scaleX * destX), srcY = std::round(scaleY * destY);
		memcpy(destData + (destY * destW + destX) * channel, srcData + (srcY * srcW + srcX) * channel, sizeof(BYTE) * channel);
	};

	auto funcDrawReconstructionArea = [destData, destW, srcW, idList, channel](int destX, int destY, double scaleX, double scaleY) -> void
	{
		int srcX = std::round(scaleX * destX), srcY = std::round(scaleY * destY);

		int lSrcX = destX < 1 ? 0 : std::ceil(scaleX * destX - scaleX), rSrcX = destX == (destW - 1) ? srcW - 1 : std::floor(scaleX * destX + scaleX);
		for (int i = lSrcX; i <= rSrcX; i++)
		{
			if (idList[srcY * srcW + i] != -1)
			{
				destData[(destY * destW + destX) * channel] = 0;
				destData[(destY * destW + destX) * channel + 1] = 0;
			}
		}
	};

	auto funcRedFullImage = [destData, destW, channel](int destX, int destY) -> void
	{
		auto redPxielIndex = (destY * destW + destX) * channel;
		if (destData[redPxielIndex] == 255 && destData[redPxielIndex + 1] == 255 && destData[redPxielIndex + 2] == 255)
		{
			destData[redPxielIndex + 1] = 0;
			destData[redPxielIndex + 2] = 0;
		}
	};

	double rx = srcW / (double)destW, ry = srcH / (double)destH;

	memcpy(destData, srcData, sizeof(BYTE) * channel);

	for (int destY = 0; destY < destH; destY++)
	{
		for (int destX = 0; destX < destW; destX++)
		{
			funcImageNearestScale(destX, destY, rx, ry);

			if (idList != nullptr)
			{
				funcDrawReconstructionArea(destX, destY, rx, ry);
			}

			if (redFull)
			{
				funcRedFullImage(destX, destY);
			}
		}
	}

	destData += (destW * destH) * channel;
}