相信大家对于二叉树的遍历并不陌生,对于二叉树的递归遍历我们也可以信手拈来。但是如果让我们将二叉树修改成为非递归的形式呢?是不是有点疑惑了?那么本次博客我们就来梳理一下二叉树的非递归遍历。
由于递归遍历二叉树的代码以及逻辑都很简单,所以我们直接给出代码的结果,之后直接进行输出结果的比较即可。
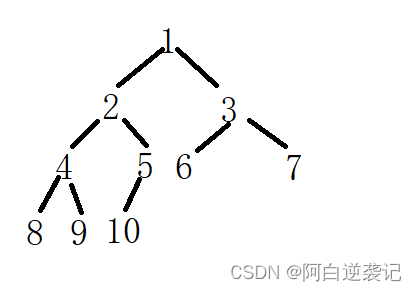
我们手动构建的树的形式如下图所示。
遍历结果如下:

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
//创建一个节点,用于创建树的节点
typedef struct BTNodeTree
{
int _val;
struct BTNodeTree* left;
struct BTNodeTree* right;
BTNodeTree(int data)
:_val(data)
,left(nullptr)
,right(nullptr)
{}
}*BTNode;
//使用递归的形式实现二叉树的前中后序遍历
void preOrder(BTNode root)
{
if (root == nullptr)
{
return;
}
cout << root->_val << " ";
preOrder(root->left);
preOrder(root->right);
}
void midOrder(BTNode root)
{
if (root == nullptr)
{
return;
}
midOrder(root->left);
cout << root->_val << " ";
midOrder(root->right);
}
void posOrder(BTNode root)
{
if (root == nullptr)
{
return;
}
posOrder(root->left);
posOrder(root->right);
cout << root->_val << " ";
}
BTNode& createTree()
{
//由于我们从堆当中申请空间,在此函数结束的时候,并不会释放栈帧,因此可以使用&返回
BTNode data1 = new BTNodeTree(1);
BTNode data2 = new BTNodeTree(2);
BTNode data3 = new BTNodeTree(3);
BTNode data4 = new BTNodeTree(4);
BTNode data5 = new BTNodeTree(5);
BTNode data6 = new BTNodeTree(6);
BTNode data7 = new BTNodeTree(7);
BTNode data8 = new BTNodeTree(8);
BTNode data9 = new BTNodeTree(9);
BTNode data10 = new BTNodeTree(10);
data1->left = data2;
data1->right = data3;
data2->left = data4;
data2->right = data5;
data3->left = data6;
data3->right = data7;
data4->left = data8;
data4->right = data9;
data5->left = data10;
return data1;
}
int main()
{
BTNode root = createTree();
cout << "preOrder:";
preOrder(root);
cout << endl;
cout << "midOrder:";
midOrder(root);
cout << endl;
cout << "posOrder";
posOrder(root);
cout << endl;
return 0;
}使用栈编写迭代形式的树的遍历
之后的内容就是我们本次博客的重头戏了。我们需要将上述的过程修改成为非递归的形式。(为了便于区分我们可以将递归的形式遍历树的操作封装到一个命名空间域当中,避免访问冲突的情况产生)根据我们所学的知识来说:所有的递归函数都会创建一个栈帧,之后以栈的形式进行访问并输出数据,以达到我们的预期效果,所以我们就可以使用栈这个数据结构模拟实现我们栈帧的开辟。
先序遍历
首先是我们的先序遍历。首先我们需要创建一个栈,之后根据我们的输出要求向栈当中压入数据。首先我们向栈中压入我们的首节点,之后根据栈是否为空进行判断是否需要继续循环。之后我们因为需要先读取左子树当中的数据,因此我们栈顶的元素应该是左子树的数据节点,那么也就是说我们需要先向栈当中加入右子树的节点。之后每一次进行循环的时候,从栈当中拿出一个数据,删除并加入其左右子树即可。过程如图所示:
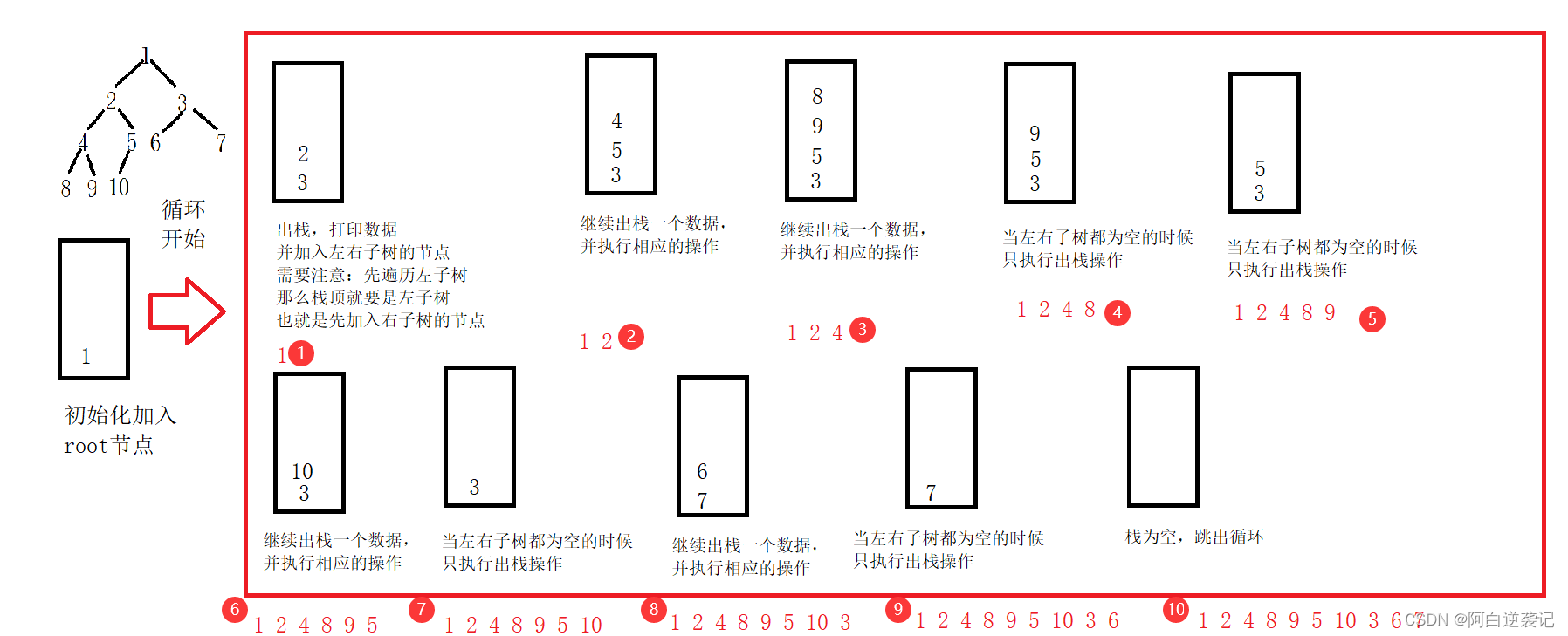
根据上述步骤我们可以编写出如下的代码:
void preOrder(BTNode root)
{
stack<BTNode> ret;
ret.push(root);
while (!ret.empty())
{
cout << ret.top()->_val << " ";
BTNode tmp = ret.top();
ret.pop();
if (tmp->right)
{
ret.push(tmp->right);
}
if (tmp->left)
{
ret.push(tmp->left);
}
}
}中序遍历
想要进行中序遍历操作,我们需要先清楚中序遍历执行遍历节点的步骤。首先我们需要先访问左子树,当左子树已经访问完毕之后才访问根节点进行打印数据。因此我们就需要设置一个指针进行遍历操作。首先我们从根节点开始,向左进行执行,如果左子树不为空就将该节点压入栈中继续访问,形成循环,当我们的左子树为空的时候,我们就需要将栈顶的元素赋值给cur,打印输出并访问右子树。过程如图所示:
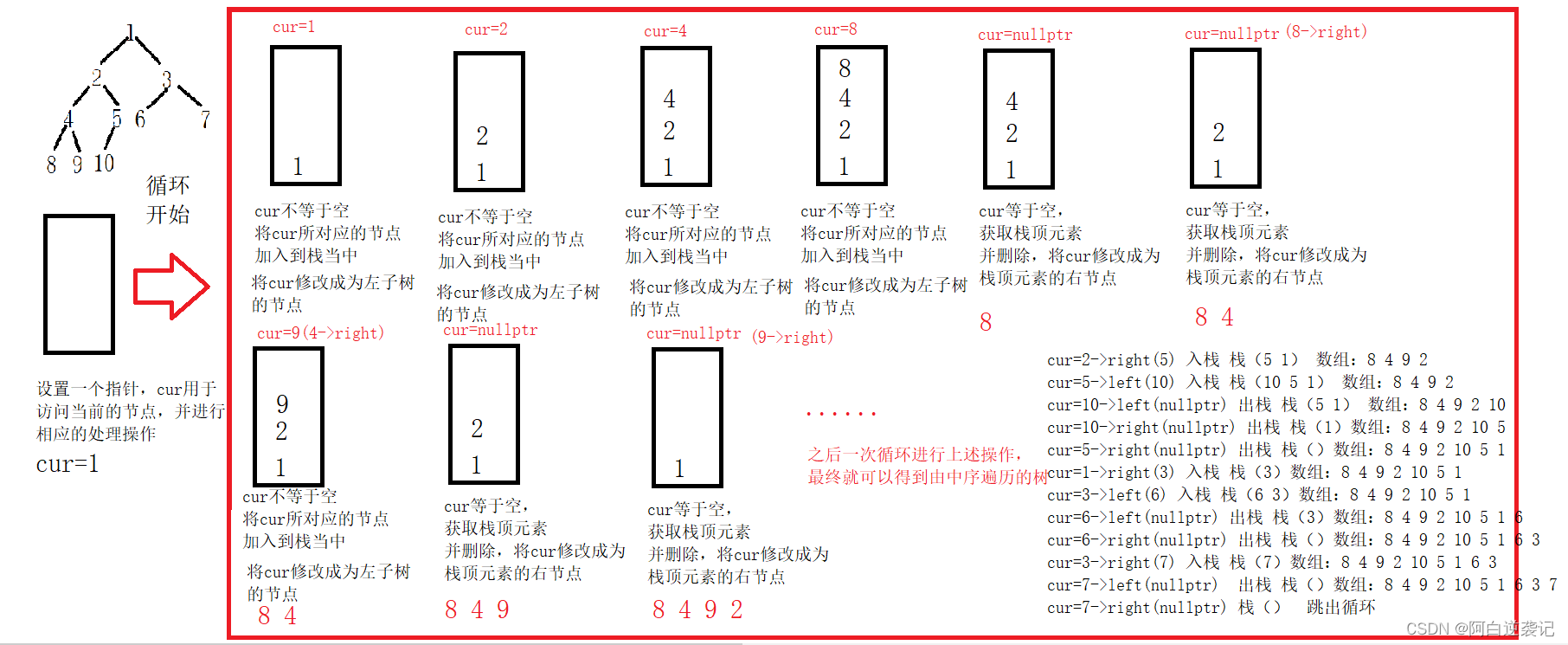
根据上述步骤我们可以编写出如下代码:
void midOrder(BTNode root)
{
stack<BTNode> ret;
BTNode cur = root;
while (cur != nullptr || !ret.empty())
{
if (cur)
{
ret.push(cur);
cur = cur->left;
}
else
{
cur = ret.top();
ret.pop();
cout << cur->_val << " ";
cur = cur->right;
}
}
}后序遍历
对于后序遍历的实现我们有两种方式。
后序遍历1:
我们可以根据后序遍历的特点进行观察,后序遍历操作会先访问左子树,之后再访问右子树,等到所有的节点都访问完毕的时候我们才会输出相应的数据。所以我们的执行顺序就为:左右根
而我们的前序遍历,我们需要进行的遍历顺序为:根左右。那是不是说我们只需要对前序遍历进行略微的修改,再进行逆序就可以得到我们后序遍历的执行效果呢?我们可以尝试编写代码:
需要注意的是:对于前序遍历我们需要修改加入栈中的节点的顺序,如果想要逆序得到左右根的话,我们正序就需要是根右左,我们就需要将栈顶元素时刻保持为右子树的状态,这是和前序遍历的唯一区别。
void posOrder1(BTNode root)
{
vector<int> data;
stack<BTNode> ret;
ret.push(root);
while (!ret.empty())
{
data.push_back(ret.top()->_val);
BTNode tmp = ret.top();
ret.pop();
if (tmp->left)
{
ret.push(tmp->left);
}
if (tmp->right)
{
ret.push(tmp->right);
}
}
reverse(data.begin(), data.end());
for (auto e : data)
{
cout << e << " ";
}
}后序遍历2:
前面的后序遍历是使用先序遍历进行复现的,那么有没有方法可以直接实现后序遍历呢?当然有了。这个方法和我们的中序遍历有些许类似之处,但是我们需要多设置几个变量进行数据的保存。
首先我们需要设置一个栈用于保存节点的数据。之后我们还需要设置一个cur指针,用于作为节点移动的标志,我们还需要设置一个prev指针,用于记录我们是否已经遍历过右边子树的节点,防止重复遍历。因为我们的遍历顺序是:左右根,根是最后访问的,那么我们就需要遍历完右子树之后再访问根节点。但是我们有需要和从根节点进入右节点当中的情况进行区分,所以我们需要设置一个prev指针进行记录。其中保存的是刚刚执行过操作的右子树的节点的指针。
我们需要进行的操作大致如下:首先我们需要找到左子树的根节点,当我们一直进行访问并将节点的指针加入到栈当中,直到遇到空节点之后。这个时候cur指向nullptr,我们需要让cur拿到栈顶的元素,也就是最近的左子树的节点,这个时候我们需要对该节点的右子树进行判断。因为我们想要先访问右子树的节点。所以如果右子树的节点不为空的时候我们需要将cur的值修改成为右子树的指针。如果为空就删除拿到的top节点。并打印输出数据。因为这个时候我们的右子树为空,也就是说应该遍历根节点了。在打印输出数据之后,就代表以该节点为根节点的树已经全部遍历完成了。那么我们就需要将prev设置成为该节点的指针,防止在执行下一次操作的时候,重复进入该子树当中造成死循环。过程如图所示:
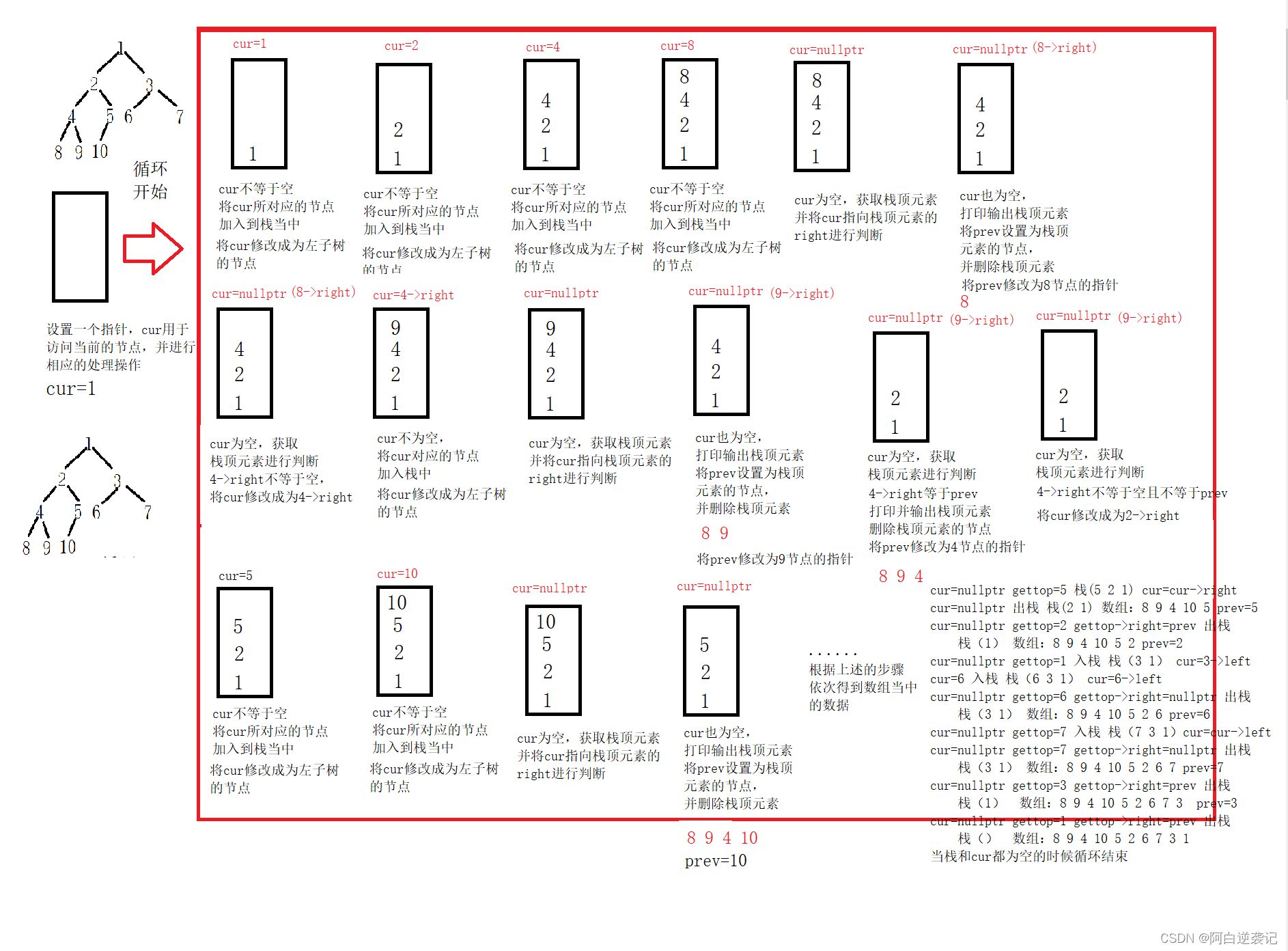
根据上述步骤我们可以编写出如下的代码:
void posOrder2(BTNode root)
{
stack<BTNode> ret;
BTNode prev = nullptr;
BTNode cur = root;
while (cur|| !ret.empty())
{
while (cur)
{
ret.push(cur);
cur = cur->left;
}
BTNode top = ret.top();
if (top->right == nullptr || top->right == prev)
{
ret.pop();
cout << top->_val << " ";
prev = top;
}
else
{
cur = top->right;
}
}
}测试一遍我们使用栈进行树的遍历的输出结果:
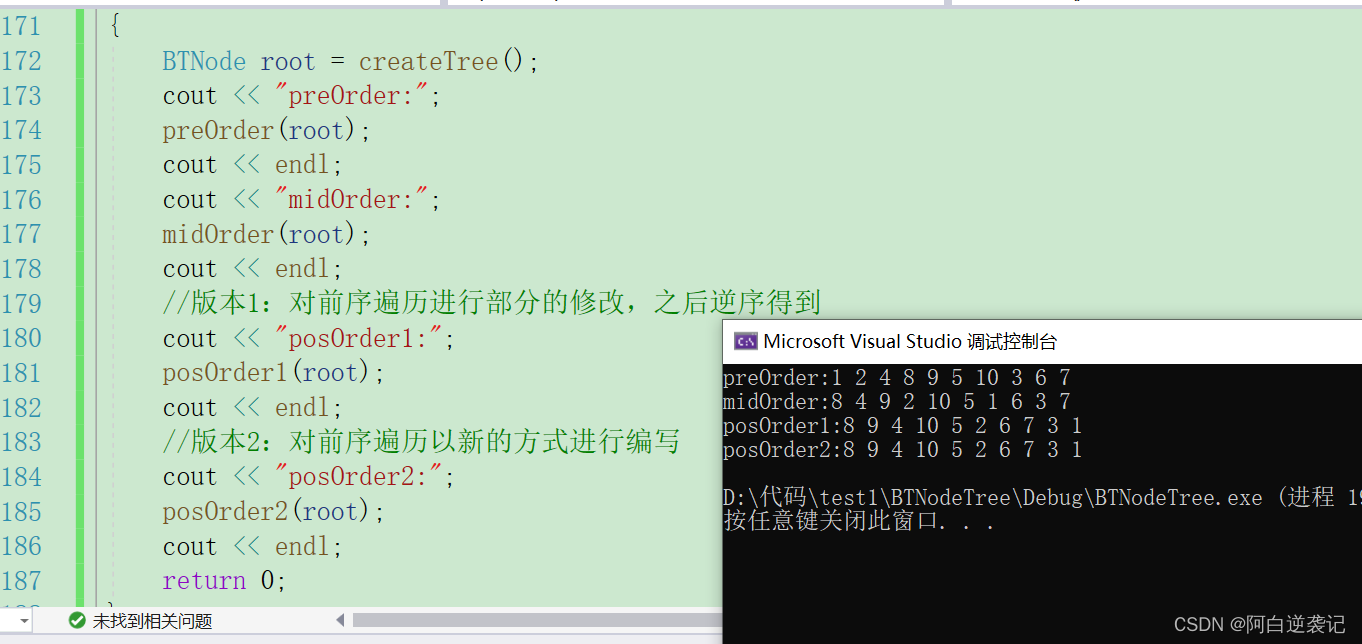
对比我们之前使用递归的形式编写的代码,结果一切正常。