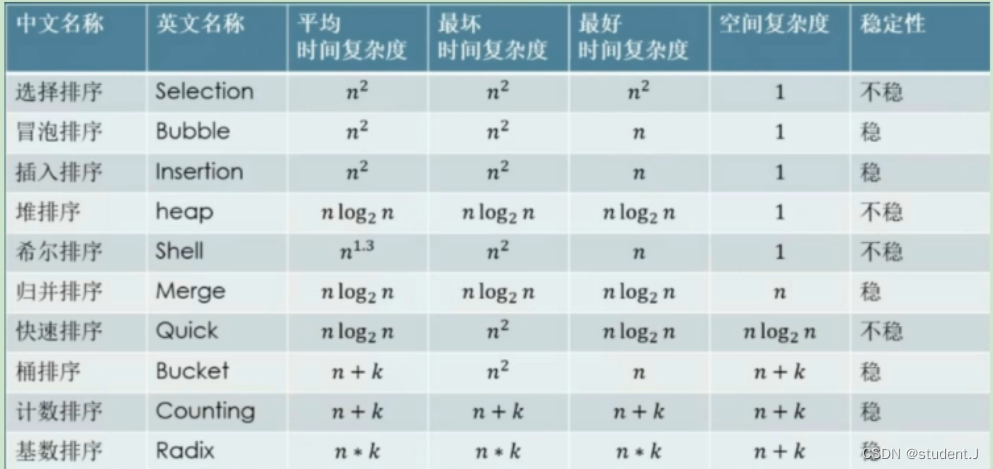
动画演示

各种算法：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
6种常见排序算法：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

1、冒泡排序

//1、冒泡排序Bubble Sort: 比较前后相邻的数据，按照升序或者降序规则调整
// 由于每次调整没有开辟新的内存空间，一直都是使用一个新内存空间，所以空间复杂度为O(1)
// 由于需要n轮调整，每轮调整 n-- 个数据，时间复杂度为O(n^2)
// data[]是int*指针，数组名，size 是数组的长度，有效数据个数
int* BubbleSort(int data[], size_t size)
{
	int max;//临时存储最大值
	//共循环n = size轮
	for (int i = 0; i < size; i++)
	{
		//每一轮操作的数据为n = size-i，循环完一轮就排好了一个数，那么需要操作的数就每次-1
		for (int j = 1; j < size - i; j++)
		{
			//如果前面的数大于后面的数，就交换，每一轮找到最大的数，并放到最后
			if (data[j-1] > data[j])
			{
				max = data[j-1];
				data[j-1] = data[j];
				data[j] = max;
			}
		}
	}
	return data;
}

2、快速排序

//快速排序QuickSort,对冒泡排序的优化
//分而自治的思想，找一个参考值，左边小于参考值，右边大于参考值，再更换参考值继续
//时间和空间复杂度为O(nlog_2 n)
int* QuickSort(int data[], int left , int right)
{
	if (left >= right)
		return data;
	int i = left;
	int j = right;
	int base = data[left];
	while ( i < j )
	{
		//此方法必须先从后面找小的，先从前面会出错
		while (data[j] >= base && (i < j))//右边边是大的就继续找到小的
			j--;
		while (data[i] <= base && (i < j))//左边是小的就继续找到大的
			i++;
		if (i < j)
		{
			int temp = data[i];
			data[i] = data[j];
			data[j] = temp;
		}
	}
	data[left] = data[i];
	data[i] = base;//将base放在中间，左边都是小的，右边是大的
	QuickSort(data, left, i-1);//先递归左边区域
	QuickSort(data, i+1, right);
	return data;
}

3、选择排序

//2、选择排序SelectSort:每一次在所有数据中找出最小值或者最大值，然后在最开始或最末尾进行交换
//需要找n = size次数据，每次找n-i个数据，时间复杂度为O(n^2),空间复杂度为O(1)
int* SelectSort(int data[], size_t size)
{
	int min, temp;//临时存储最小值和最小值所在的下标
	for (int i = 0; i < size; i++)
	{
		min = data[i];//把需要交换的位置做好标记
		temp = i;
		for (int j = i + 1; j < size; j++)
		{
			if (data[j] < min)
			{
				min = data[j];//如果找到新的最小值，做好标记
				temp = j;
			}
		}
		data[temp] = data[i];//进行位置的交换，如果当前就是最小值，返回自己
		data[i] = min;
	}
	return data;
}

4、插入排序

//3、直接插入排序InsertSort:每次从后面新增一个数据，然后排好序再新增数据
//新增n = size-1个数据，新增了之后重排i+1个数据，时间复杂度O(n^2),空间复杂度O(1)
int* InsertSort(int data[], size_t size)
{
	int temp;
	for (int i = 0; i < size - 1; i++)
	{
		for (int j = i + 1; j > 0; j--)//每次从后面新增一个数据，并判断大小
		{
			if (data[j] < data[j - 1])//如果后面的值大于前面的就交换
			{
				temp = data[j-1];
				data[j - 1] = data[j];
				data[j] = temp;
			}
		}
	}
	return data;
}

5、希尔排序

//4、希尔排序SheelSort，对插入排序的优化
//时间复杂度O(n^1.3),空间复杂度O(1)
int* SheelSort(int data[], size_t size)
{
	int temp;
	size_t gap = size / 2;
	while (gap > 0)//最小间隔为1
	{
		for (size_t i = gap; i < size; i++)//从第一个间隔位置开始
		{
			size_t j = i;
			while ((j>=gap)&&(data[j]<data[j-gap]))//插入排序
			{
				temp = data[j - gap];
				data[j - gap] = data[j];
				data[j] = temp;
				j -= gap;//如果当前位置超过了2倍gap，还需要继续判断，相当于插入排序
			}
		}
		gap /= 2;//每次将gap减半
	}
	return data;
}