文章目录
- 图的简介
- 图的定义
- 图的结构
- 图的分类
- 无向图
- 有向图
- 带权图（Wighted Graph）
- 图的存储
- 邻接矩阵（Adjacency Matrix）
- 邻接表
- 代码实现
- 图的遍历
- 深度优先搜索（DFS，Depth Fisrt Search）
- 遍历抖索过程
- 广度优先搜索（BFS，Breadth First Search）
- 遍历搜索过程
- 完整代码
图的简介
图的定义
图（Graph）一种比线性表和树更加复杂的结构。在图形结构中，顶点（vertex）之间的关系是任意的，途中任意两个顶点之间都有可能关联。
图的结构
- 顶点（vertex）：图中的元素，就叫做顶点。如图：ABCDEF。
- 边（edge）: 顶点之间建立的连接关系，就叫做边。如图：顶点A和顶点B中间的连线。
- 度（drgree）: 跟顶点相连的边的条数，就叫做度。如图：顶点A与B、C、D相连，则A的度就是3。
图的分类
无向图
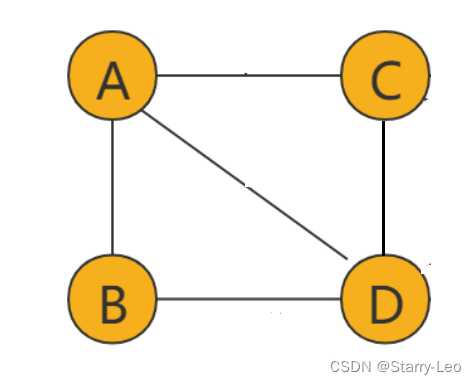
如上图，边（edge）没有方向的图叫做无向图。
有向图
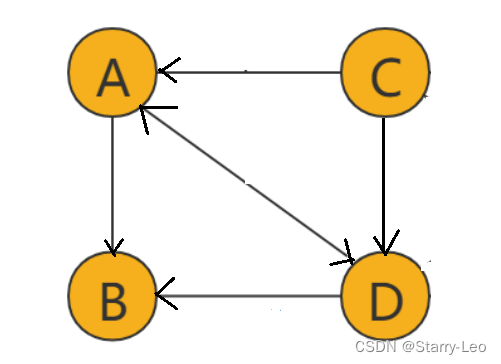
如上图，边（edge）有方向的图叫做有向图。
带权图（Wighted Graph）
如上图中，每条边都带有一个权重（weight）的图，就是带权图。
图的存储
邻接矩阵（Adjacency Matrix）
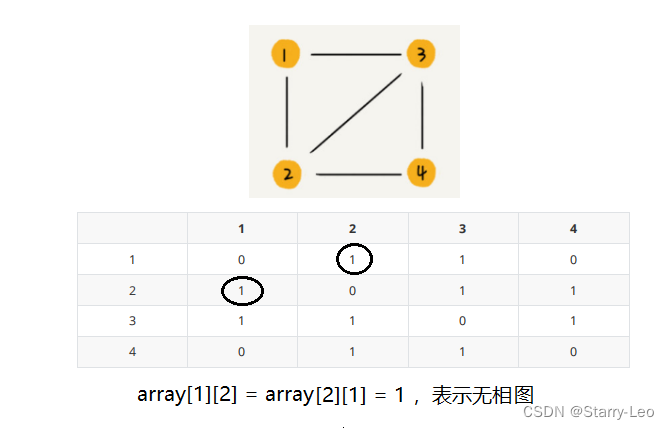
邻接矩阵的底层是一个二维数组，如下图，该图可以转化为一个二维数据表格。
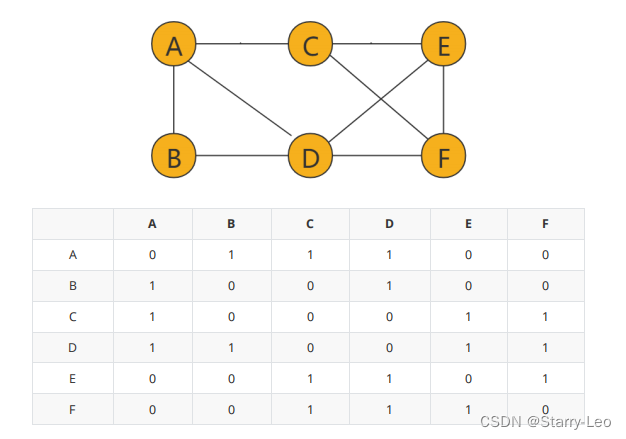
- 无向图
如果顶点 i 和顶点 j 之间有边但是没有方向和权重，那么我们就用array[i][j] = array[j][i] = 1，来表示无向图。
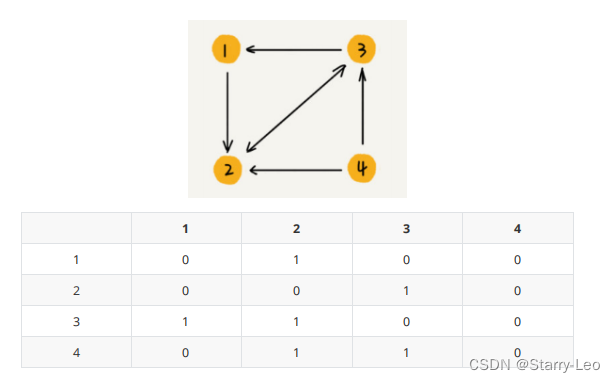
- 有向图
如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j]标记为 1。同理，如果有一条箭头从顶点 j 指向顶点 i 的边，我们就将 A[j][i]标记为 1。
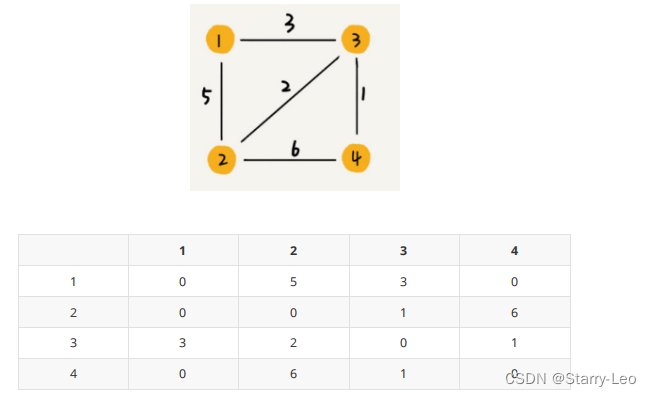
- 带权图
数组中就存储相应值当作权重。
邻接表
邻接表中每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。
图中的一个有向图的邻接表的存储方式，前面的数组存储的是所有的顶点，每个顶点后面链接的块代表：前面顶点所指向的顶线和边的权值。如果该点还有其它顶点，则继续在块后面添加即可。
代码实现
定点（Vertex）类：
package com.xxliao.datastructure.graph;
/**
* @author xxliao
* @description: 图 - 定点类
* @date 2024/5/29 16:56
*/
public class Vertex {
// 顶点名称
protected String name;
// 该顶点出发的边
protected Edge edge;
public Vertex(String name, Edge edge) {
this.name = name;
this.edge = edge;
}
}
边（Edge）类：
package com.xxliao.datastructure.graph;
/**
* @author xxliao
* @description: 图 - 边类
* @date 2024/5/29 16:57
*/
public class Edge {
// 被指向的顶点
protected String name;
// 权重
protected int weight;
// 顶点的下一条边
protected Edge next;
public Edge(String name, int weight, Edge next) {
this.name = name;
this.weight = weight;
this.next = next;
}
}
图（Graph）类：
package com.xxliao.datastructure.graph;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
* @author xxliao
* @description: 邻接表实现图
* @date 2024/5/29 16:00
*/
public class Graph {
// 存储顶点容器
private Map<String,Vertex> vertexes;
public Graph() {
this.vertexes = new HashMap<String,Vertex>();
}
/**
* @description 添加顶点
* @author xxliao
* @date 2024/5/29 17:02
*/
public void addVertex(String vertexName) {
vertexes.put(vertexName,new Vertex(vertexName,null));
}
/**
* @description 添加边
* @author xxliao
* @date 2024/5/29 17:05
*/
public void addEdge(String beginVertexName,String endVertexName,int weight) {
// 获取出发顶点
Vertex beginVertex = vertexes.get(beginVertexName);
if(beginVertex == null) {
// 没有开始顶点，创建
beginVertex = new Vertex(beginVertexName,null);
vertexes.put(beginVertexName,beginVertex);
}
// 创建边对象
Edge edge = new Edge(endVertexName,weight,null);
if(beginVertex.edge == null) {
//当前顶点还没有边，直接设置
beginVertex.edge = edge;
}else {
Edge lastEdge = beginVertex.edge;
while(lastEdge.next != null) {
lastEdge = lastEdge.next;
}
// 设置到末尾
lastEdge.next = edge;
}
}
}
图的遍历
图的遍历是指，从给定图的任意顶点（可以称为初始顶点）出发，按照某种搜索方法沿着图边访问所有的顶点，且每个顶点仅被访问一次，这个过程就是图的遍历。图的遍历根据搜索过程不用，可以分为深度优先搜索和广度优先搜索。
深度优先搜索（DFS，Depth Fisrt Search）
深度优先搜索，从起点出发，从规定的方向中选择一个方向，不段的往前走，直到无法继续位置，然后尝试另外一个方向，直到最后走完所有顶点。
遍历抖索过程
假设我们有这么一个图，里面有A、B、C、D、E、F、G、H 8 个顶点，点和点之间的联系如下图所示：
必须依赖栈（Stack），特点是后进先出（LIFO）。
-
第一步，选择一个起始顶点，例如从顶点 A 开始。把 A 压入栈，标记它为访问过（用红色标记），并输出到结果中。
-
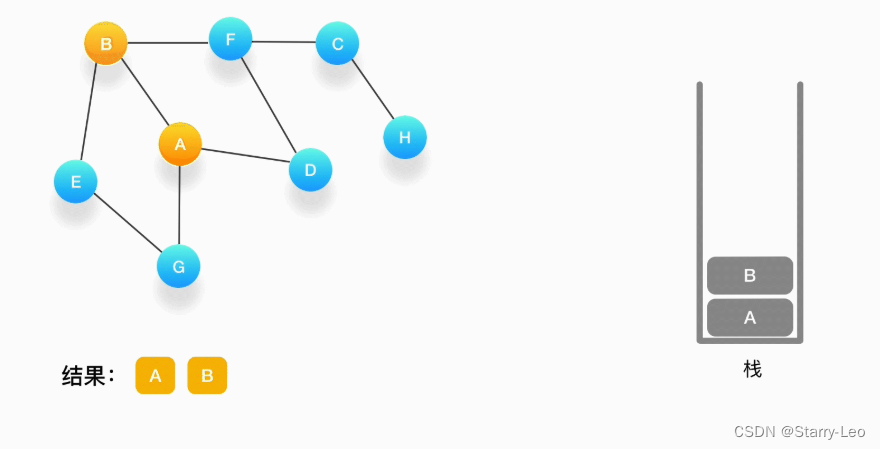
第二步，寻找与 A 相连并且还没有被访问过的顶点，顶点 A 与 B、D、G 相连，而且它们都还没有被访问过，我们按照字母顺序处理，所以将 B 压入栈，标记它为访问过，并输出到结果中。
-
第三步，现在我们在顶点 B 上，重复上面的操作，由于 B 与 A、E、F 相连，如果按照字母顺序处理的话，A 应该是要被访问的，但是 A 已经被访问了，所以我们访问顶点 E，将 E 压入栈，标记它为访问过，并输出到结果中。
-
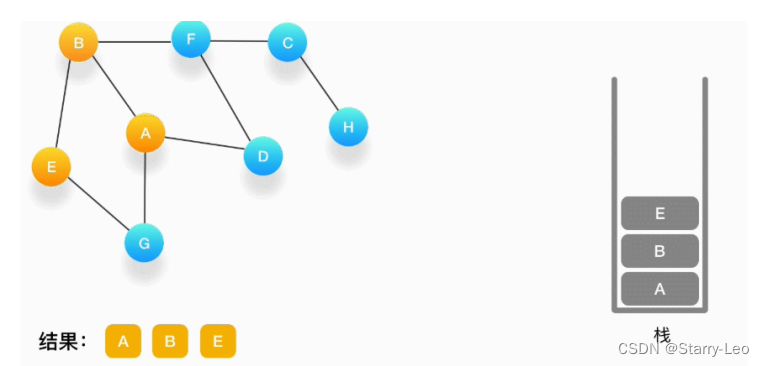
第四步，从 E 开始，E 与 B、G 相连，但是B刚刚被访问过了，所以下一个被访问的将是G，把G压入栈，标记它为访问过，并输出到结果中。
-
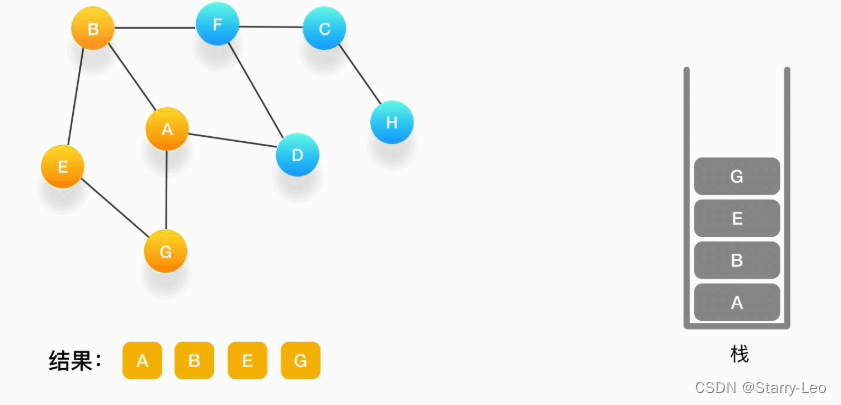
第五步，现在我们在顶点 G 的位置，由于与 G 相连的顶点都被访问过了，类似于我们走到了一个死胡同，必须尝试其他的路口了。所以我们这里要做的就是简单地将 G 从栈里弹出，表示我们从 G 这里已经无法继续走下去了，看看能不能从前一个路口找到出路。
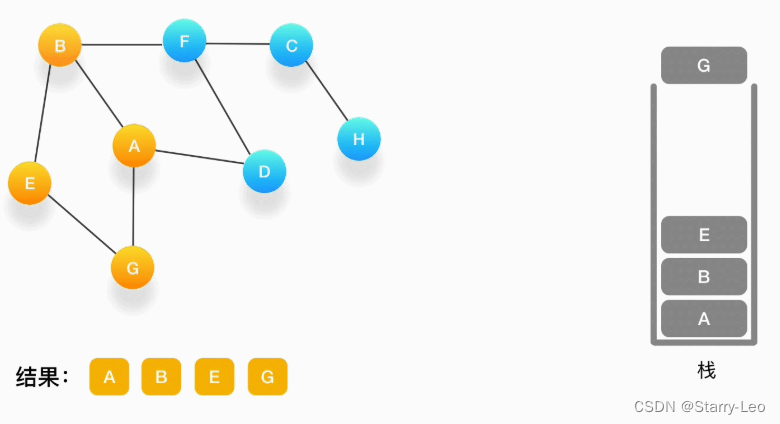如果发现周围的顶点都被访问了，就把当前的顶点弹出。 -
第六步，现在栈的顶部记录的是顶点 E，我们来看看与 E 相连的顶点中有没有还没被访问到的，发现它们都被访问了，所以把 E 也弹出去。
-
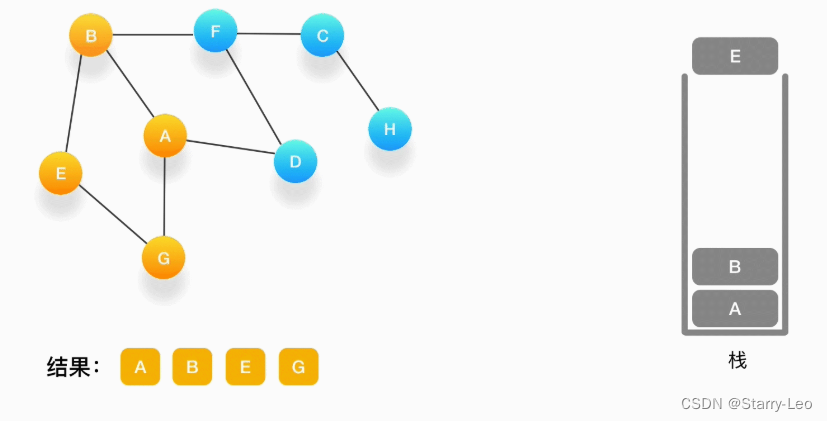
第七步，当前栈的顶点是 B，看看它周围有没有还没被访问的顶点，有，是顶点 F，于是把 F 压入栈，标记它为访问过，并输出到结果中。
-
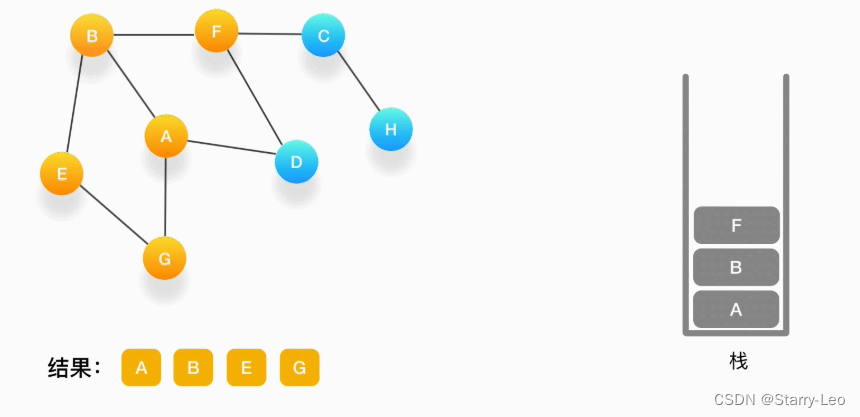
第八步，当前顶点是 F，与 F 相连并且还未被访问到的点是 C 和 D，按照字母顺序来，下一个被访问的点是 C，将 C 压入栈，标记为访问过，输出到结果中。
-
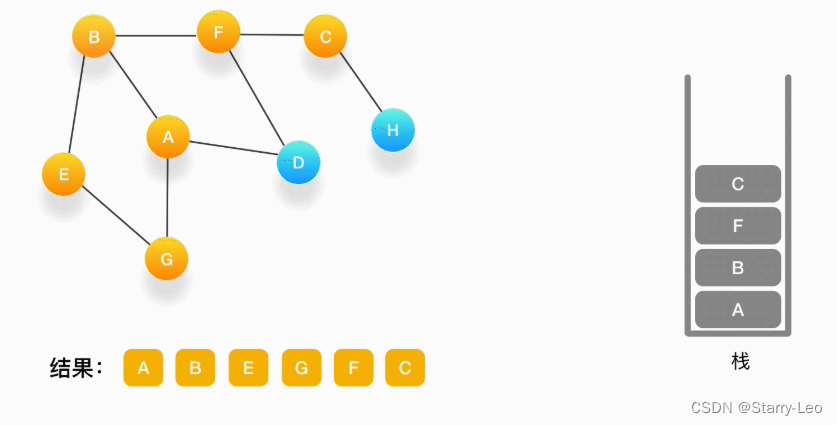
第九步，当前顶点为 C，与 C 相连并尚未被访问到的顶点是 H，将 H 压入栈，标记为访问过，输出到结果中。
-
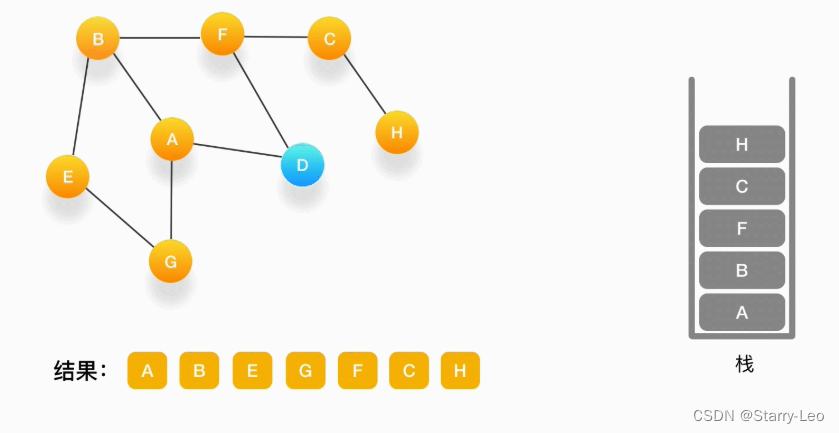
第十步，当前顶点是 H，由于和它相连的点都被访问过了，将它弹出栈。
-
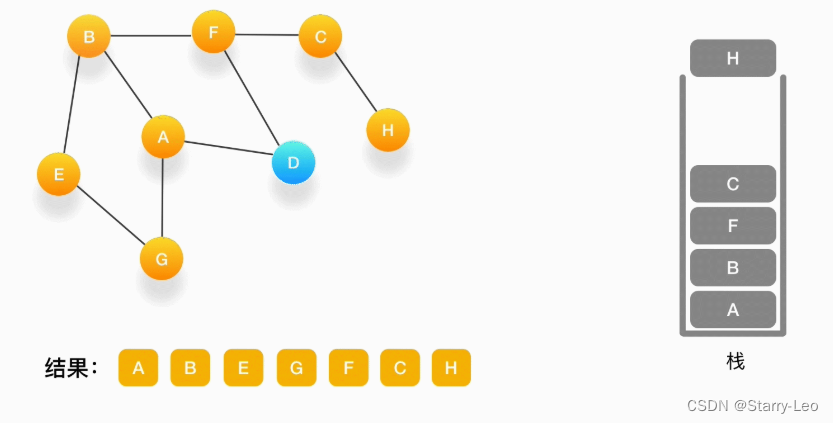
第十一步，当前顶点是 C，与 C 相连的点都被访问过了，将 C 弹出栈。
-
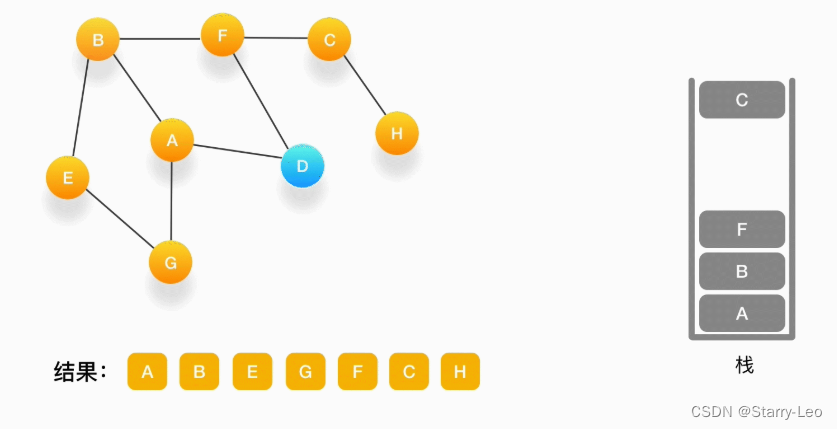
第十二步，当前顶点是 F，与 F 相连的并且尚未访问的点是 D，将 D 压入栈，输出到结果中，并标记为访问过。
-
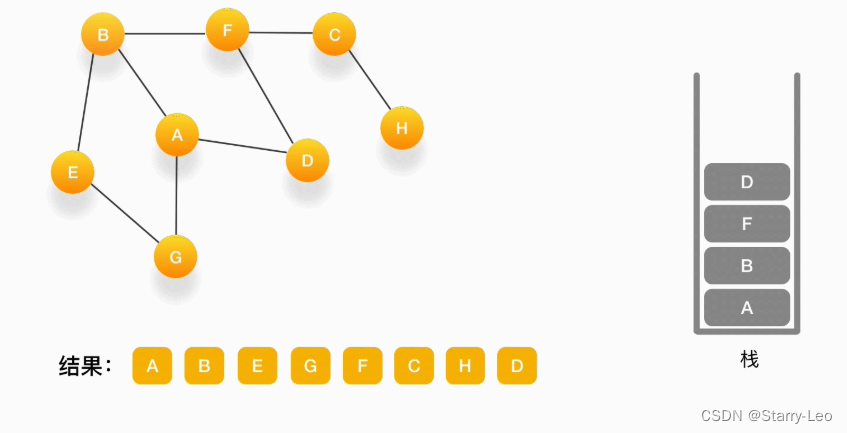
第十三步，当前顶点是 D，与它相连的点都被访问过了，将它弹出栈。以此类推，顶点 F，B，A 的邻居都被访问过了，将它们依次弹出栈就好了。最后，当栈里已经没有顶点需要处理了，我们的整个遍历结束。
广度优先搜索（BFS，Breadth First Search）
遍历搜索过程
假设我们有这么一个图，里面有A、B、C、D、E、F、G、H 8 个顶点，点和点之间的联系如下图所示，
对这个图进行深度优先的遍历。
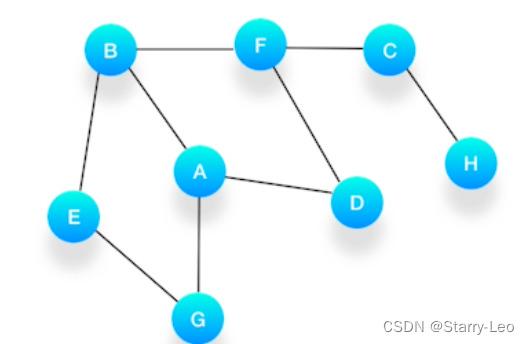
依赖队列（Queue），先进先出（FIFO）。
一层一层地把与某个点相连的点放入队列中，处理节点的时候正好按照它们进入队列的顺序进行。
- 第一步，选择一个起始顶点，让我们从顶点 A 开始。把 A 压入队列，标记它为访问过（用红色标记）。
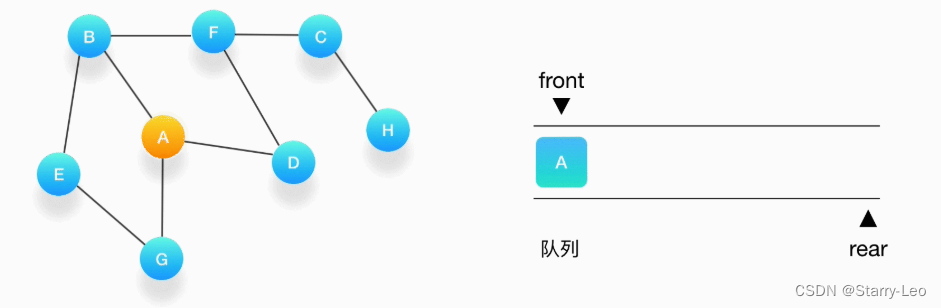
- 第二步，从队列的头取出顶点 A，打印输出到结果中，同时将与它相连的尚未被访问过的点按照字母大
小顺序压入队列，同时把它们都标记为访问过，防止它们被重复地添加到队列中。
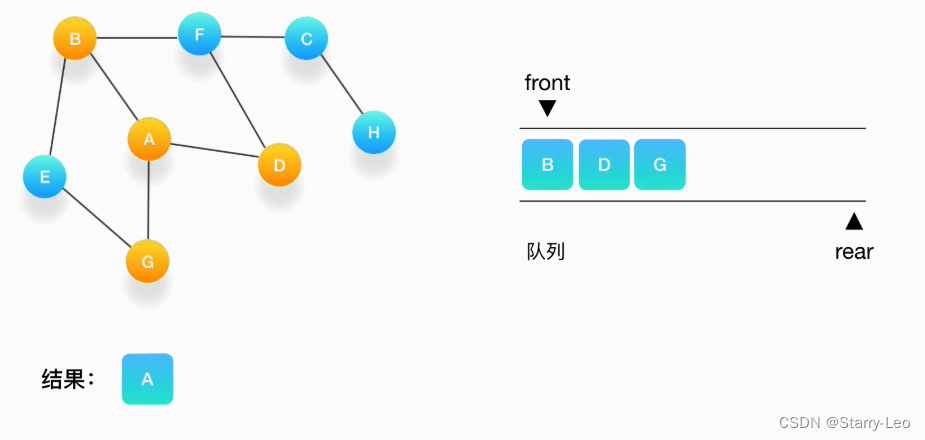
- 第三步，从队列的头取出顶点 B，打印输出它，同时将与它相连的尚未被访问过的点（也就是 E 和 F）
压入队列，同时把它们都标记为访问过。
- 第四步，继续从队列的头取出顶点 D，打印输出它，此时我们发现，与 D 相连的顶点 A 和 F 都被标记
访问过了，所以就不要把它们压入队列里。
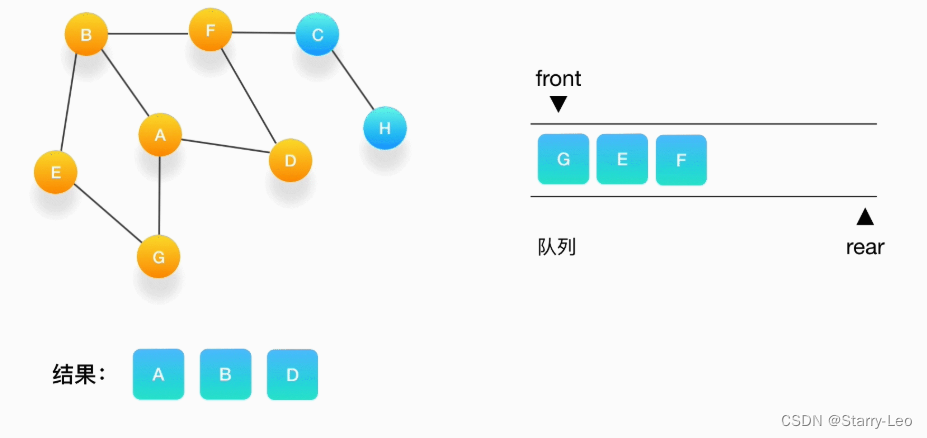
- 第五步，接下来，队列的头是顶点 G，打印输出它，同样的，G 周围的点都被标记访问过了。我们不做
任何处理。
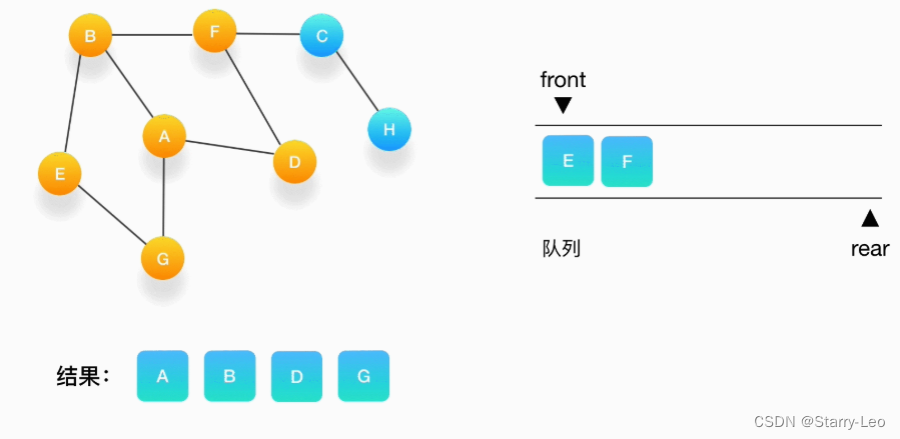
- 第六步，队列的头是 E，打印输出它，它周围的点也都被标记为访问过了，我们不做任何处理。
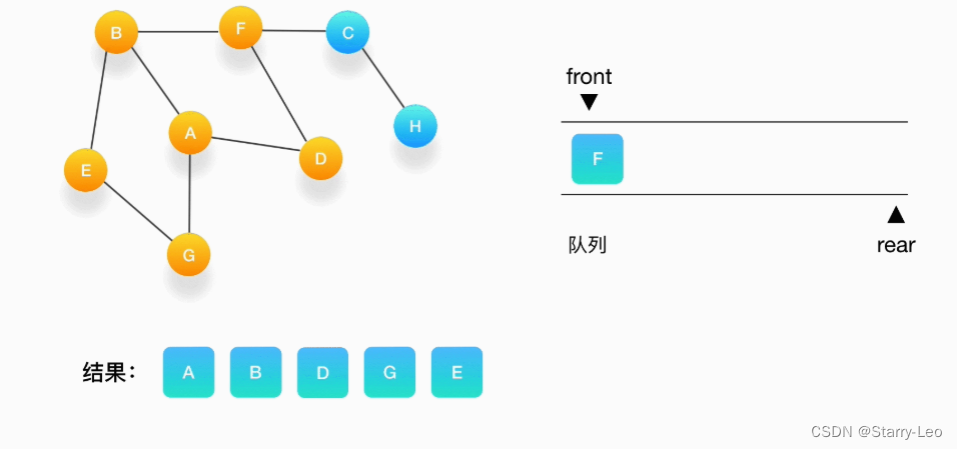
- 第七步，接下来轮到顶点 F，打印输出它，将 C 压入队列，并标记 C 为访问过。
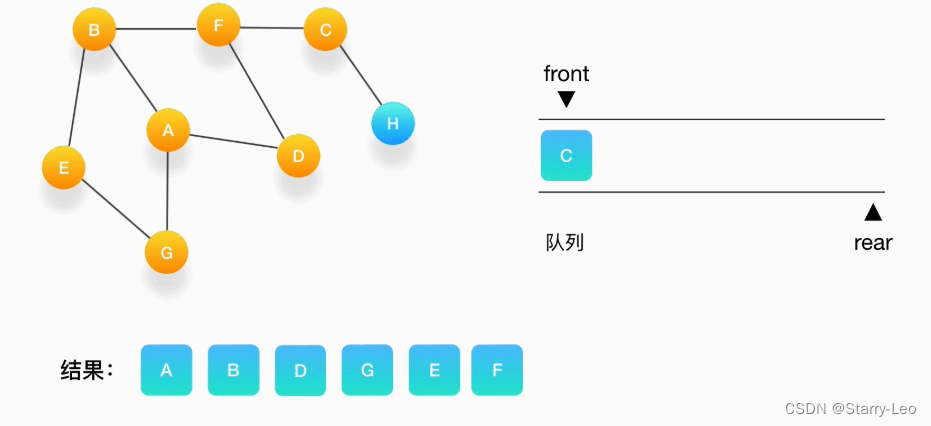
- 第八步，将 C 从队列中移出，打印输出它，与它相连的 H 还没被访问到，将 H 压入队列，将它标记为
访问过。
9.第九步，队列里只剩下 H 了，将它移出，打印输出它，发现它的邻居都被访问过了，不做任何事情。
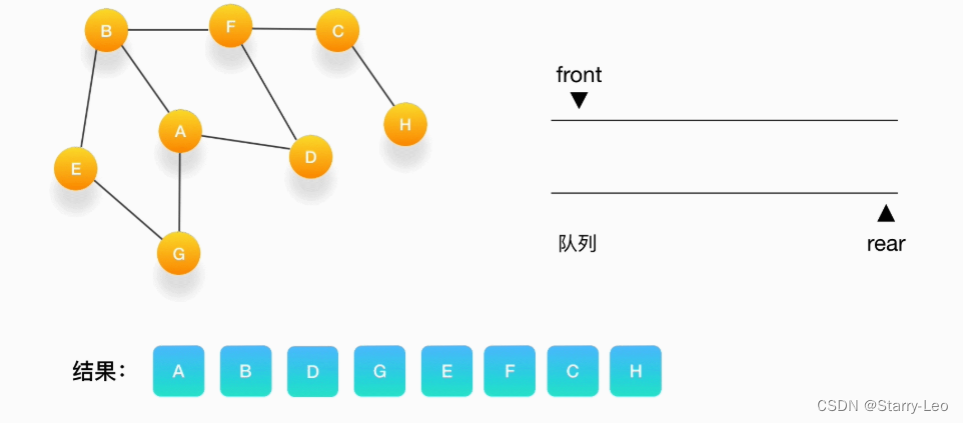
- 第十步，队列为空，表示所有的点都被处理完毕了，程序结束。
完整代码
https://github.com/xxliao100/datastructure_algorithms.git
