由浅入深二叉树刷题指南与讲解

news2024/11/15 11:26:52

目录

  • 前言
  • 二叉树OJ基础题目
    • 1. 单值二叉树
    • 2. 检查两棵树是否相同
    • 3. 二叉树的前中后序遍历
    • 4. 另一棵树的子树
    • 5. 对称二叉树
    • 6. 二叉树的构建以及遍历
  • 二叉树其他方法的实现
    • 1. 二叉树的销毁
    • 2. 层序遍历
    • 3. 判断二叉树是否是完全二叉树
  • 二叉树的其他性质
  • 总结

前言

上一篇我们已经了解了二叉树的实现方式, 那么本篇重在进入二叉树OJ刷题环节, 我也会分享我在写题的思路, 帮助我们更好的理解二叉树, 并且本篇也进行二叉树其他方法的实现, 也欢迎不同观点评论区留言.

博客主页: 酷酷学!!!
创作不易, 感谢关注~

在这里插入图片描述

二叉树OJ基础题目

1. 单值二叉树

题目链接: 单值二叉树

题目描述:

在这里插入图片描述
在这里插入图片描述
题目分析:

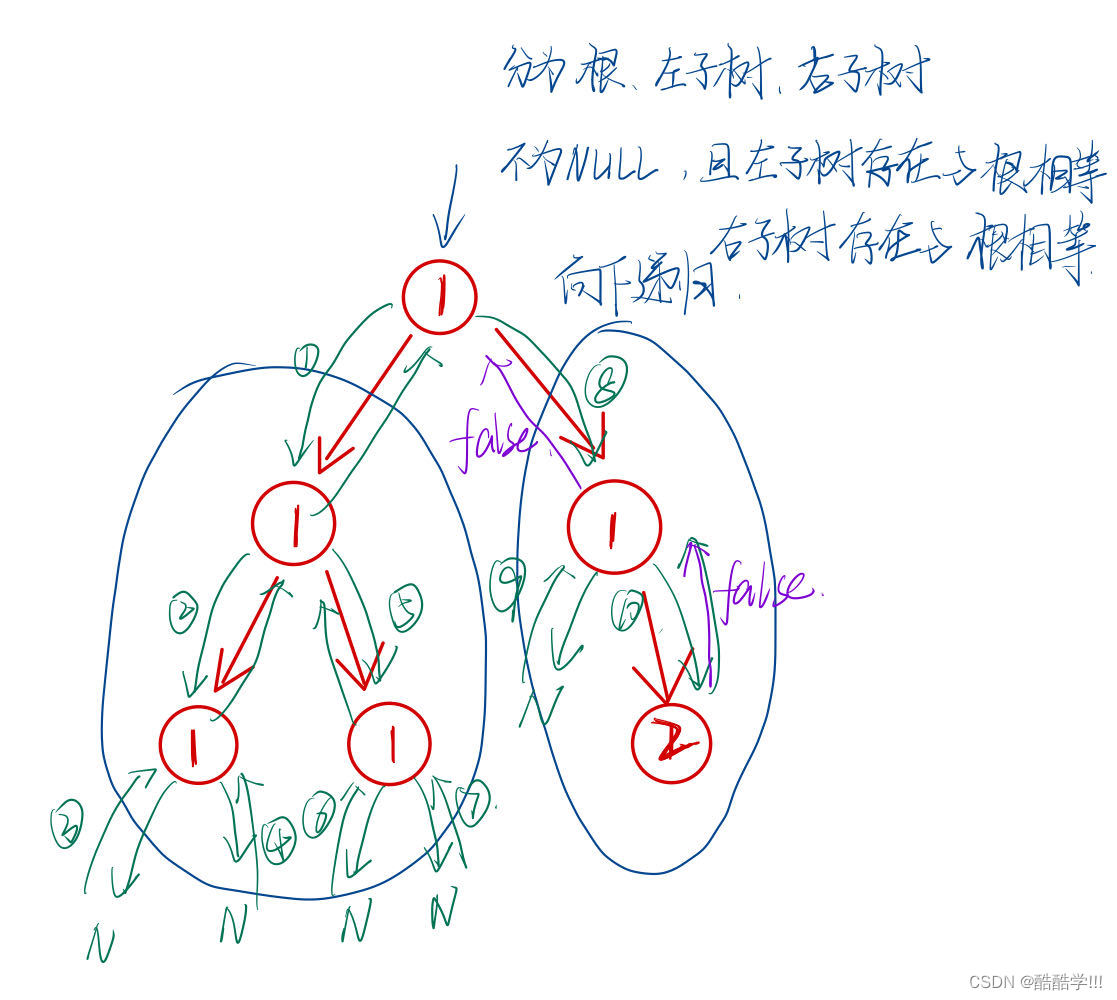
首先此题是要求判断一棵二叉树是否为单值二叉树, 也就是说每一个结点的值是否都相等, 因为二叉树递归定义的, 所以这里我们也可以采用递归的思路去解题, 二叉树可以分为根和子树, 可以判断根和子树是否相等, 然后递归进行判断子树的根和子树是否相等. 如果相等就继续下一层递归, 如果不相等就直接返回false.

判断条件是如果一颗树的左子树存在且值和根不相等, 或者右子树存在且根和右子树的值不相等, 则返回false, 如果判断到的子树为NULL,则说明其他子树都与根结点相同.

在这里插入图片描述

代码如下:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    if(root==NULL)
    {
        return true;
    }
    if(root->left && root->val != root->left->val)
    {
        return false;
    }
    if(root->right && root->val !=root->right->val)
    {
        return false;
    }
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

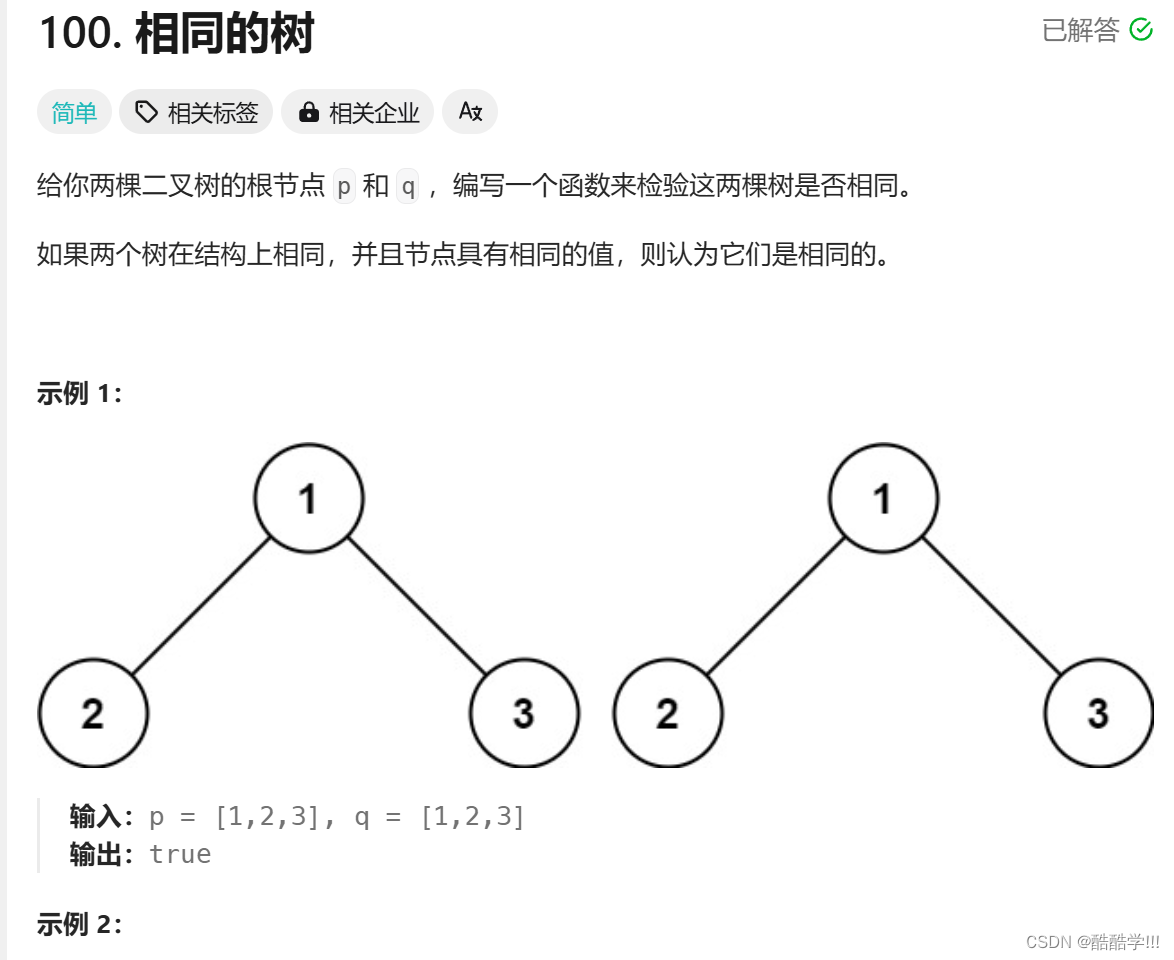
2. 检查两棵树是否相同

题目链接: 相同的树

题目描述:

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
代码如下:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left) && 
    isSameTree(p->right,q->right);
}

代码分析:

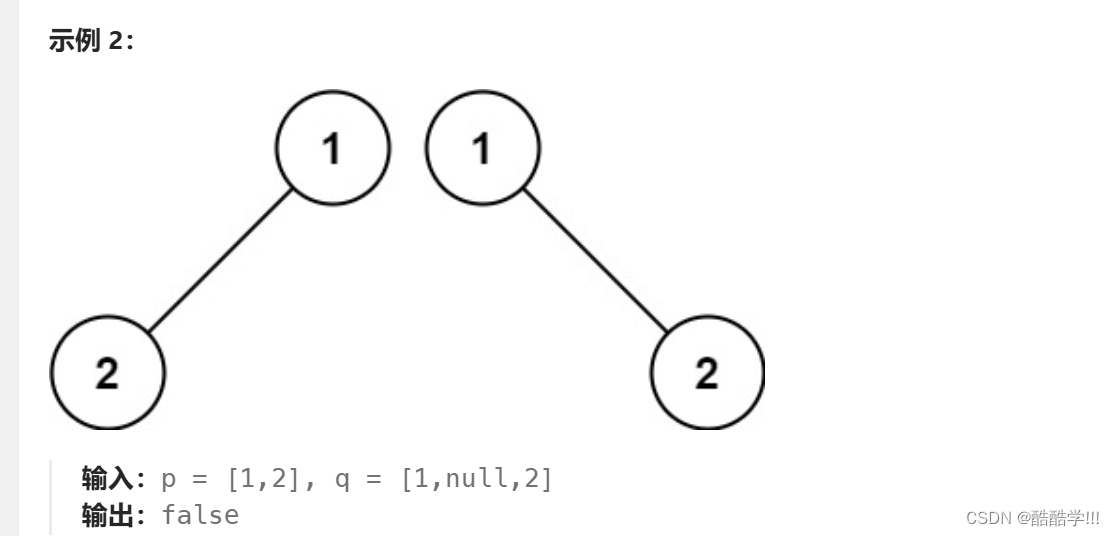
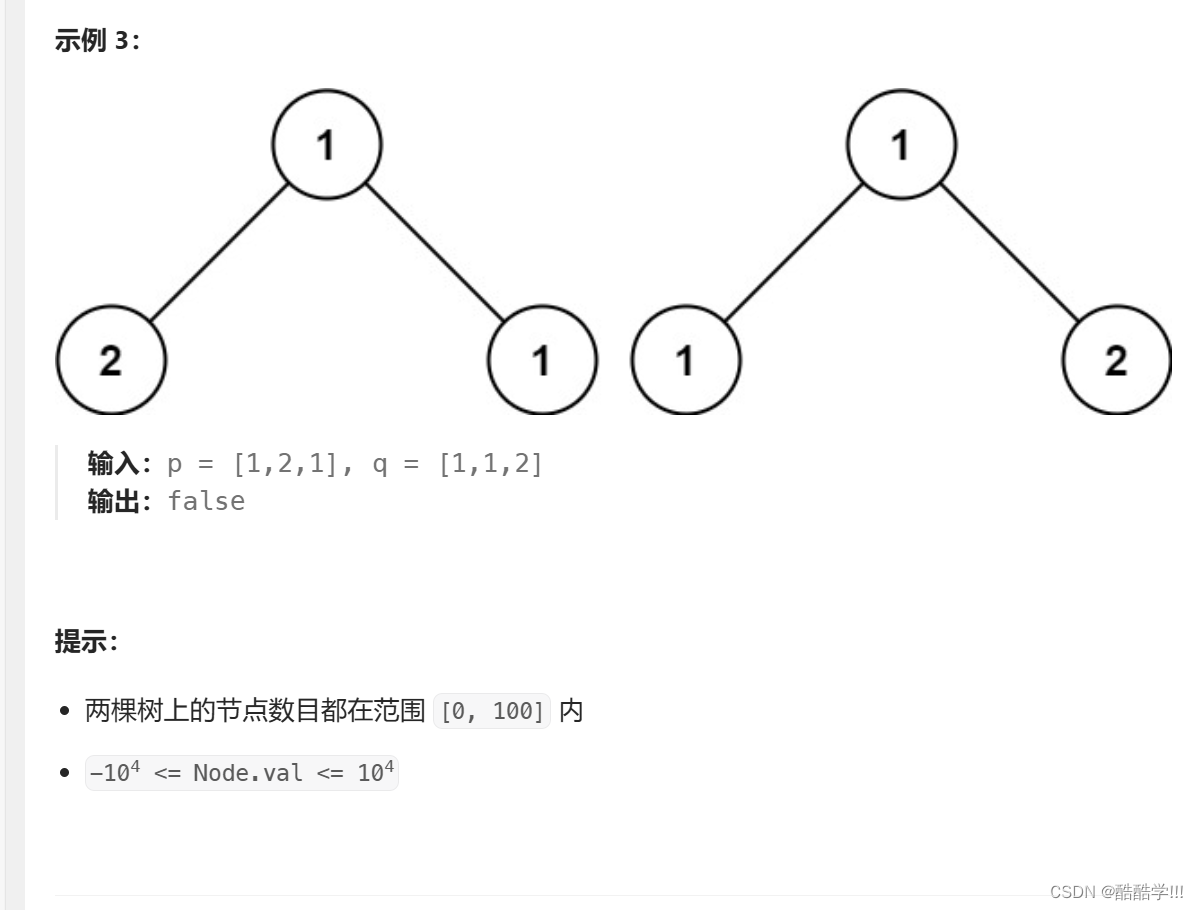
递归比较子树的根结点是否相同, 如果两个根都为空, 则表示已经比较到叶子节点的下一层, 则其它结点都比较完毕, 说明相同, 如果一个结点为NULL,另一个不为NULL,则一定不相同, 然后比较根节点是否相同, 不相同返回false,相同则继续递归比较.子树的左树和右树都相同, 则说明两棵树相同.

3. 二叉树的前中后序遍历

题目链接:

前序遍历
中序遍历
后序遍历

这里以前序遍历做讲解, 其他遍历题目解题方法类似

题目描述:

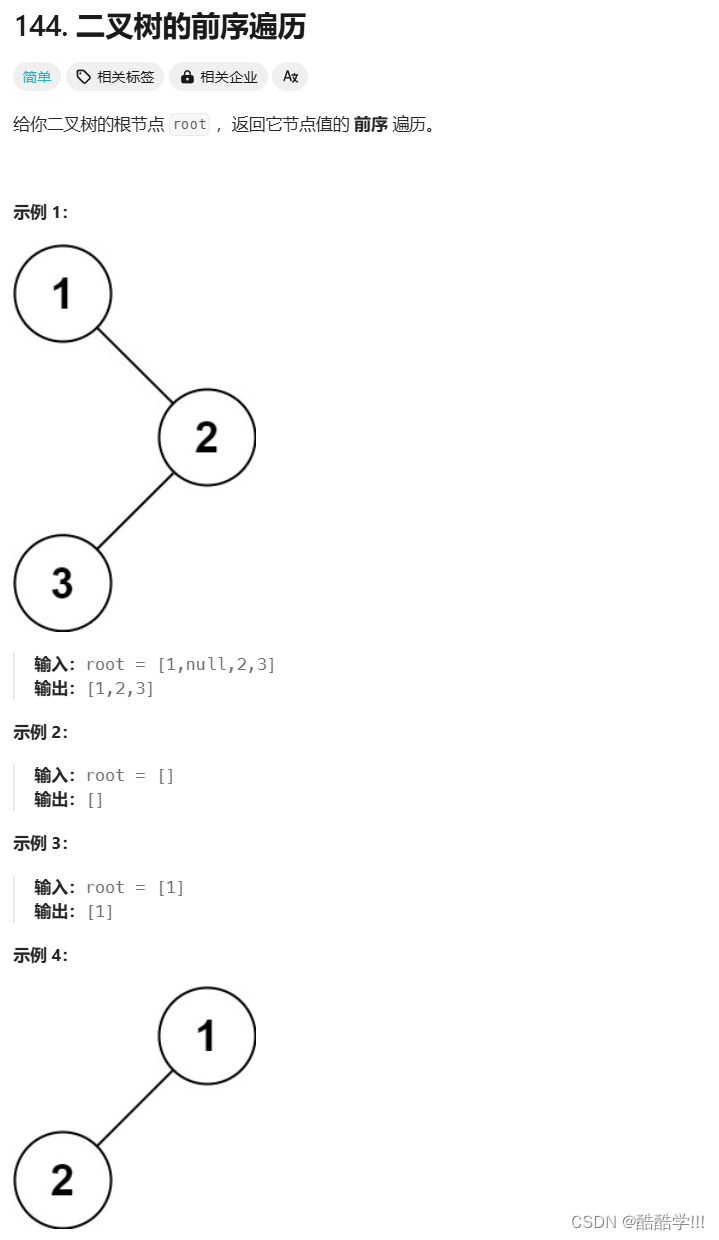
在这里插入图片描述

代码如下:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0: TreeSize(root->left) + TreeSize(root->right) + 1; 
}

void PrevOrder(struct TreeNode* root,int* arr,int* i)
{
    if(root==NULL)
    {
        return;
    }
    arr[*i] = root->val;
    (*i)++;
    PrevOrder(root->left,arr,i);
    PrevOrder(root->right,arr,i);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    PrevOrder(root,arr,&i);
    return arr;
}

代码解析:

首先*returnSize表示的是数组元素的个数, 这里传递过来的是一个指针类型变量, 因为函数外面可能会用到这个值, 想要改变只能传递实参, 题目要求遍历的结果存放在数组中, 因为我们不知道开辟多大空间, 所以可以先求一下结点个数, 也比较简单, 然后用returnSIze接收一下, 接着创建数组, 进行前序遍历, 需要另外定义一个函数, 因为遍历二叉树需要递归, 所以不可以直接递归函数, 因为不能每次都开辟一个数组, 递归结构存放在数组中, 然后返回数组即可.

4. 另一棵树的子树

题目链接: 另一棵树的子树

题目描述:

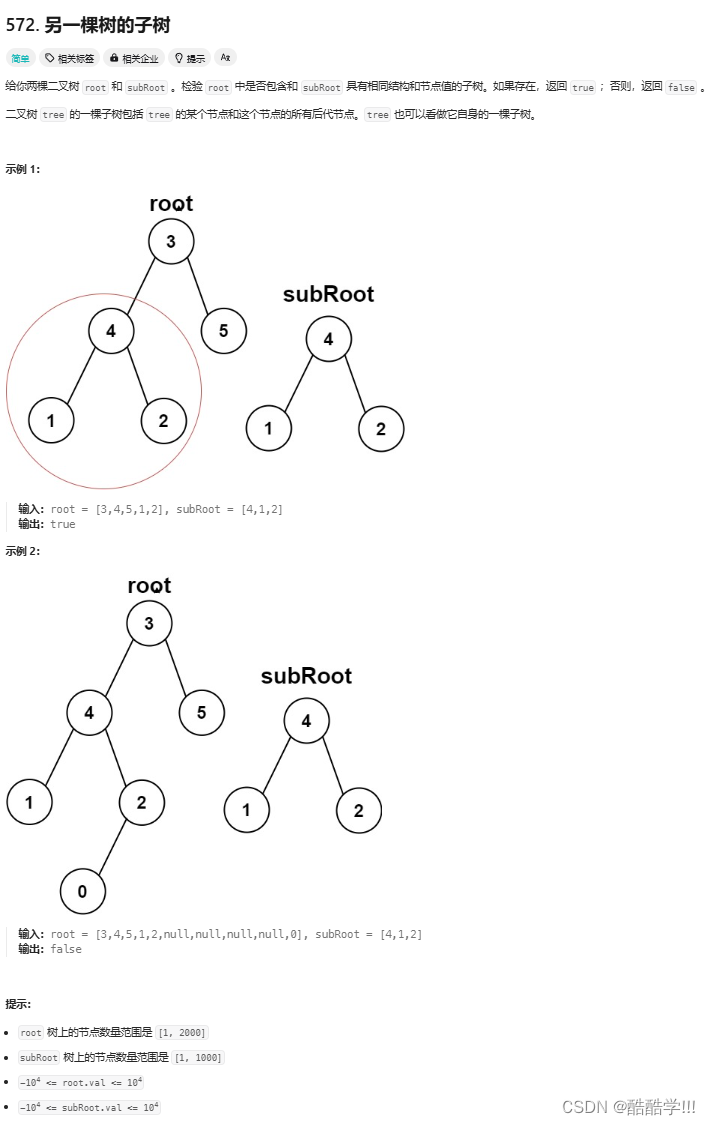
在这里插入图片描述
代码如下:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isSameTree(struct TreeNode* p,struct TreeNode* q)
{
    if(p==NULL && q==NULL)
    {
        return true;
    }
    if(p==NULL || q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left) && 
    isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root==NULL)
    {
        return false;
    }
    if( isSameTree(root,subRoot))
    {
        return true;
    }
    return isSubtree(root->left,subRoot) || 
    isSubtree(root->right,subRoot);
}

代码分析:

判断一棵树是否是另一棵树的子树, 也就是root的子树是否和subroot相同, 我们只需判断每一棵root的子树和subroot相同即可, 这里我们用到了上面写的代码, 判断两棵树是否相同, 这里我们需要依次去递归调用左子树和右子树与subroot进行判断, 只要有一棵树相同就说明为另一棵树的子树, 如果判断到NULL了,则说明遍历了所有子树的根都无法找到与之相同的树, 则不为另一棵树的子树.

5. 对称二叉树

题目链接: 对称二叉树

题目描述:

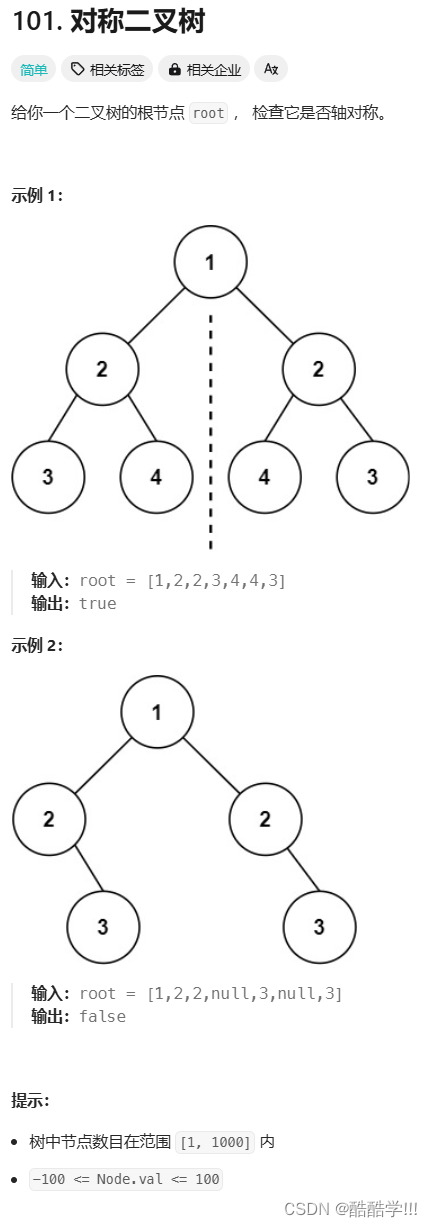
在这里插入图片描述
代码如下:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool _isSameTree(struct TreeNode* left,struct TreeNode* right)
{
    if(left == NULL && right == NULL)
    {
        return true;
    }
    if(left == NULL || right == NULL)
    {
        return false;
    }
    if(left->val != right->val)
    {
        return false;
    }
    return _isSameTree(left->left,right->right)
    &&_isSameTree(left->right,right->left);

}


bool isSymmetric(struct TreeNode* root) {
    return _isSameTree(root->left,root->right);
}

代码解析:

对称二叉树, 则就是比较这棵树的两个子树, 左子树的左孩子是否和右子树的有孩子是否相同, 左子树的右孩子是否和右子树的左孩子相同, 我们可以使用判断两个相同的树的代码进行改写, 只不过传递参数不同.

6. 二叉树的构建以及遍历

题目链接: 二叉树的构建以及遍历

题目描述:

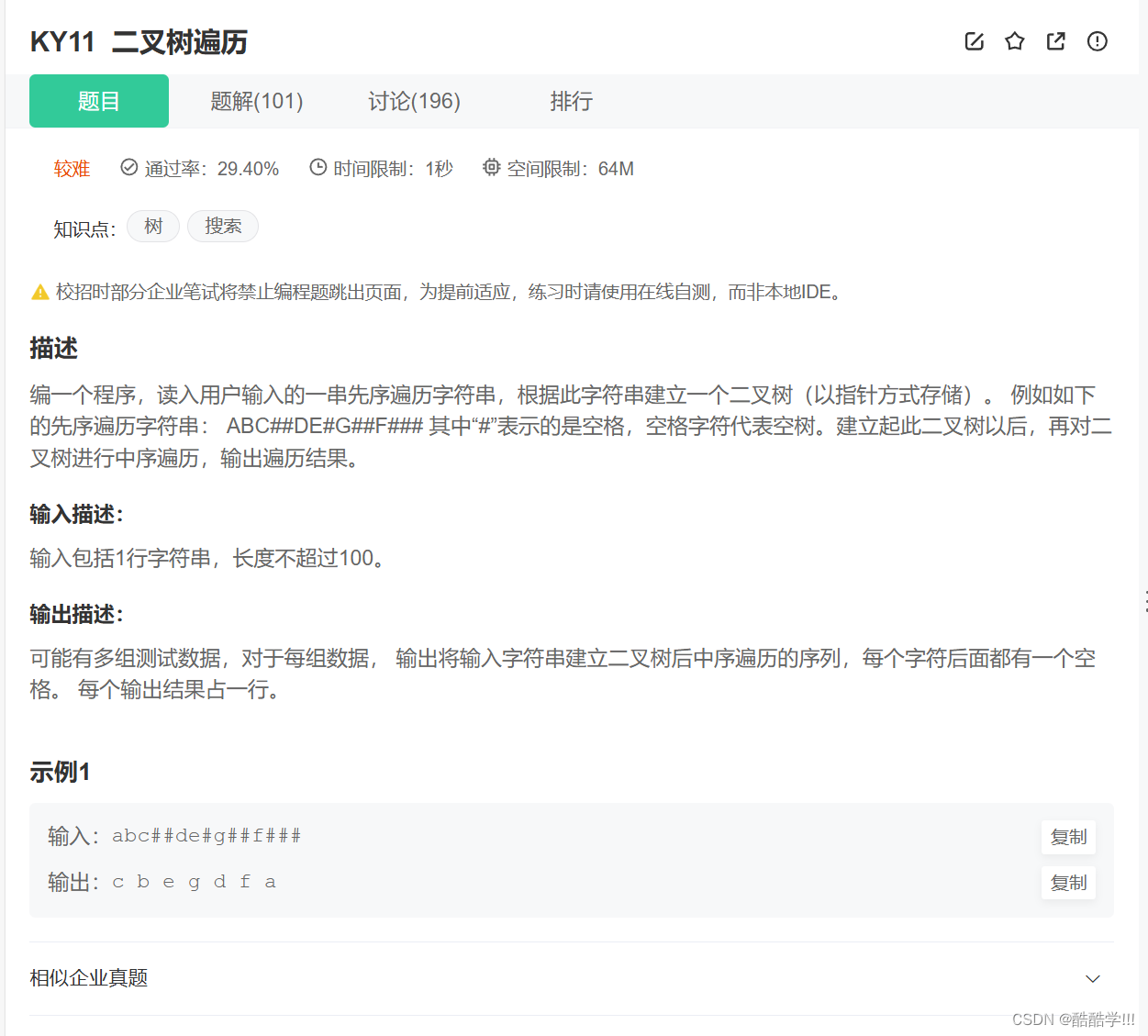
在这里插入图片描述

代码如下:

#include <stdio.h>
#include<stdlib.h>

typedef char Datatype;
typedef struct BTnode
{
    struct BTnode* left;
    struct BTnode* right;
    Datatype val;
}BTnode;

BTnode* CreateTree(char* str,int* pi)
{
    if(str[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    BTnode* newnode = (BTnode*)malloc(sizeof(BTnode));
    newnode->val = str[*pi];
    (*pi)++;
    newnode->left = CreateTree(str,pi);
    newnode->right = CreateTree(str, pi);
    return newnode;
}

void InOrder(BTnode* root)
{
    if(root == NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}

int main() {
    char str[100] = {0};
    scanf("%s",str);
    int i = 0;
    BTnode* root = CreateTree(str,&i); 
    InOrder(root);
    return 0;
}

代码分析:

首先题目给定一个字符串, 这个字符串是先序遍历的, 需要我们创建一个二叉树, 然后中序遍历输出, 首先我们读取输入到的字符串到字符数组中, 然后创建二叉树, 使用递归进行创建, 定义一个树的结点, 每次申请一个结点, 如果读取到’#'则跳过, 进行下一次读取, 然后存到val中, 依次创建左子树右子树, 最后中序遍历并且打印.

二叉树其他方法的实现

1. 二叉树的销毁

这里销毁一棵二叉树肯定要先从子树进行销毁, 不然销毁了根, 就无法找到子树的结点, 递归进行销毁操作, 代码如下

void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

2. 层序遍历

所谓层序遍历就是一层一层的输出, 如下图这棵树, 层序遍历的结果为1 2 3 4 5 6, 这里层序遍历, 我们可以创建一个队列, 存放树的指针, 先让根节点入队列, 每次出队列, 若孩子结点不为空, 则入队, 队列为空, 则所有结点都出队列完毕, 出队列并且打印对头元素指向的树的值

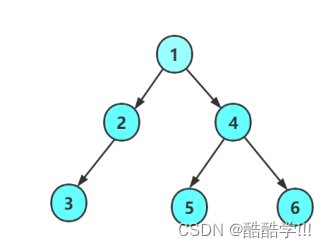
在这里插入图片描述

代码如下:

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* Front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", Front->val);
		if (Front->left)
		{
			QueuePush(&q, Front->left);
		}
		if (Front->right)
		{
			QueuePush(&q, Front->right);
		}
	}
	QueueDestroy(&q);
}

3. 判断二叉树是否是完全二叉树

这里我们走层序遍历, 因为层序遍历二叉树, 非空和空一定都是连续的, 这里我们不管空还是非空结点都入队列, 如果出队列到第一个NULL,则说明所有结点都以及入队列, 包括其孩子结点, 然后开始判断, 后面是否全是空, 是空则是完全二叉树, 不是空则不是完全二叉树.
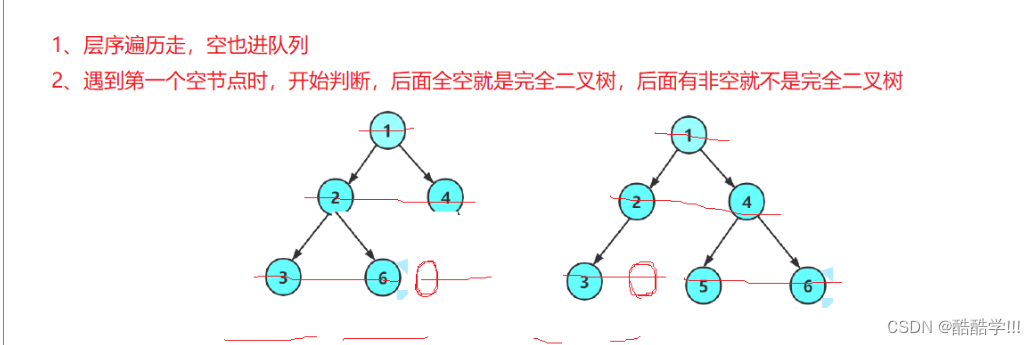
在这里插入图片描述
代码如下:

bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* Front = QueueFront(&q);
		QueuePop(&q);
	
		if (Front == NULL)
		{
			break;
		}
		QueuePush(&q, Front->left);

		QueuePush(&q, Front->right);

	}
	while (!QueueEmpty(&q))
	{
		BTNode* Front = QueueFront(&q);
		QueuePop(&q);
		if (Front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

二叉树的其他性质

在这里插入图片描述
其中性质3我们可以来分析一下, 一棵树初始状态 n0表示度为0的结点, n1表示度为1的结点, n2表示度为2的结点, 初始时为一个节点, 则n0 = 1 , n2 = 0, 增加结点, 向下插入, 每增加一个度为1的结点, 度为1的结点一定是由一个度为0的结点变过来的, 增加一个度为0, 减少一个度为0 ,则只是影响了度为1的结点, 增加一个度为2的结点,则度为1的结点变成度为2的结点, 一等增加一个度为0的结点, 减少一个度为1的结点, 依次只有增加一个度为2的结点才会影响度为0的结点个数, 并且一直保持初始状态.

在这里插入图片描述

总结

本篇旨在介绍二叉树初学者刷题题目讲解与接上篇二叉树其他方法的实现, 以及二叉树其他性质, 如果此文有帮助, 创作不易, 感谢关注.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1714328.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

整理三维空间内4点的209个结构

整理三维空间内4点的209个结构

4点的209个结构按照旋转对称的关系可分成73组 如1&#xff0c;72&#xff0c;177为一组, z y x z y x 1 72 177 1 2 10 93 4 * 4 74 39 2 * 3 73 179 5 * 5 76 178 3 * 6 75 133 6 7 77 180 7 8 8 89 34 9 11 95 35 * 35 91 …
阅读更多...
编译安装MySQL服务（LAMP2）

编译安装MySQL服务（LAMP2）

目录 1.初始化设置&#xff0c;将安装mysql 所需软件包传到/opt目录下 &#xff08;1&#xff09;关闭防火墙 &#xff08;2&#xff09;上传软件包到/opt目录 2.安装环境依赖包 3.配置软件模块 4.编译及安装 5.创建mysql用户 6.修改mysql 配置文件 7.更改mysql安装目…
阅读更多...
AB实验人群定向HTE模型1 - Causal Tree

AB实验人群定向HTE模型1 - Causal Tree

背景 论文给出基于决策树估计实验对不同用户的不同影响。并提出Honest&#xff0c;variance Penalty算法旨在改进CART在tree growth过程中的过拟合问题。 我们举个例子&#xff1a;科研人员想衡量一种新的降血压药对病人的效果&#xff0c;发现服药的患者有些血压降低但有些血…
阅读更多...
APP逆向之调试的开启

APP逆向之调试的开启

很基础的一个功能设置&#xff0c;大佬轻喷。 背景 在开始进行对APP逆向分析的时候&#xff0c;需要对APP打开调试模式。 打开调试的模式有多种方式可以通过直接改包方式也可以通过借助第三方工具进行打开调试模式。 下面就整理下这个打开调试模式的一些方式。 改包修改模…
阅读更多...
vue+element-ui时间级联动态表单，新增行，删除行，表单验证

vue+element-ui时间级联动态表单，新增行，删除行，表单验证

需求背景： 需要实现配置一种时间去执行定时任务，可能是每年一次，每月一次，每周一次，每天一次四种情况，最少配置一条，最多配置五条。年，月，周，日，时分秒是级联关系。点击提交，整体表单校验。 效果图 代码实现，具体看里面的注释 完整代码 <template><e…
阅读更多...
elastich运维

elastich运维

Elastichsearch是一种高度可扩展的开源全文搜索和分析引擎&#xff0c;可以用来实现快速、高效的数据检索。 集群规划与部署&#xff1a;首先需要根据业务需求规划Elastichsearch集群的节点数量和角色&#xff08;如主节点、副本节点、协调节点等&#xff09;。在部署时&#x…
阅读更多...
深度学习创新点不大但有效果，可以发论文吗？

深度学习创新点不大但有效果，可以发论文吗？

深度学习中创新点比较小&#xff0c;但有效果&#xff0c;可以发论文吗&#xff1f;当然可以发&#xff0c;但如果想让编辑和审稿人眼前一亮&#xff0c;投中更高区位的论文&#xff0c;写作永远都是重要的。 那么怎样“讲故事”才能让论文更有吸引力&#xff1f;我总结了三点…
阅读更多...
QT7_视频知识点笔记_67_项目练习（页面以及对话框的切换，自定义数据类型，DB数据库类的自定义及使用）

QT7_视频知识点笔记_67_项目练习（页面以及对话框的切换，自定义数据类型，DB数据库类的自定义及使用）

视频项目&#xff1a;7----汽车销售管理系统&#xff08;登录&#xff0c;品牌车管理&#xff0c;新车入库&#xff0c;销售统计图表&#xff09;-----项目视频没有&#xff0c;代码也不全&#xff0c;更改项目练习&#xff1a;学生信息管理系统。 学生信息管理系统&#xff1…
阅读更多...
智能除螨—wtn6040-8s语音芯片方案引领除螨仪新时代

智能除螨—wtn6040-8s语音芯片方案引领除螨仪新时代

语音螨仪开发背景&#xff1a; 随着物联网技术的快速发展&#xff0c;除螨仪作为家庭清洁的重要工具&#xff0c;其智能化、人性化的设计成为提升市场竞争力的关键。置入语音芯片的除螨仪&#xff0c;通过开机提示、工作状态反馈、操作指引、故障提醒等内容。用户可以更加直观…
阅读更多...
文献解读-群体基因组第二期|《中国人群中PAX2新生突变的检测及表型分析：一项单中心研究》

文献解读-群体基因组第二期|《中国人群中PAX2新生突变的检测及表型分析：一项单中心研究》

关键词&#xff1a;应用遗传流行病学&#xff1b;群体测序&#xff1b;群体基因组&#xff1b;基因组变异检测&#xff1b; 文献简介 标题&#xff08;英文&#xff09;&#xff1a;Detection of De Novo PAX2 Variants and Phenotypes in Chinese Population: A Single-Cente…
阅读更多...
AI智能分析技术与安防视频融合当前面临的困难与挑战

AI智能分析技术与安防视频融合当前面临的困难与挑战

人工智能与安防视频的融合为现代安全领域带来了革命性的变化&#xff0c;提高了安全管理水平、降低了管理成本并为用户提供了更加便捷和高效的服务。随着技术的不断进步和应用场景的不断拓展&#xff0c;未来人工智能与安防的融合将展现出更加广阔的发展前景。然而&#xff0c;…
阅读更多...
Pi 母公司将开发情感 AI 商业机器人；Meta 科学家：Sora 不是视频生成唯一方向丨RTE 开发者日报 Vol.214

Pi 母公司将开发情感 AI 商业机器人；Meta 科学家：Sora 不是视频生成唯一方向丨RTE 开发者日报 Vol.214

开发者朋友们大家好&#xff1a; 这里是 「RTE 开发者日报」 &#xff0c;每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE&#xff08;Real-Time Engagement&#xff09; 领域内「有话题的新闻」、「有态度的观点」、「有意思的数据」、「有思考的文章」、「…
阅读更多...
不用写采集规则的网页采集软件

不用写采集规则的网页采集软件

传统的网页采集工具采集网页数据&#xff0c;需要查看和研究网页代码&#xff0c;编写复杂繁琐的采集规则&#xff0c;对于有技术基础的人&#xff0c;配置一个采集规则也要花费不少时间&#xff0c;更何况对于不懂技术的普通用户来说&#xff0c;简直是一项不太可能完成的任务…
阅读更多...
开源表单流程设计器有哪几个突出的优势特点？

开源表单流程设计器有哪几个突出的优势特点？

当前&#xff0c;传统的表单制作已经无法满足现在企业的发展需求了。想要实现高效率发展&#xff0c;需要引进先进的低代码技术平台、开源表单流程设计器等优秀软件平台助力发展。它们具有可视化操作界面、灵活好操作、易维护、效率高等诸多优势特点&#xff0c;在推动企业实现…
阅读更多...
如何使用 .htaccess 删除文件扩展名

如何使用 .htaccess 删除文件扩展名

本周有一个客户&#xff0c;购买Hostease的虚拟主机&#xff0c;询问我们的在线客服&#xff0c;如何使用 .htaccess 删除文件扩展名&#xff1f;我们为用户提供相关教程&#xff0c;用户很快解决了遇到的问题。在此&#xff0c;我们分享这个操作教程&#xff0c;希望可以对您有…
阅读更多...
Docker化Spring Boot3应用：从镜像构建到部署

Docker化Spring Boot3应用：从镜像构建到部署

随着容器化技术的发展&#xff0c;越来越多的应用采用了容器化部署的方式。容器化部署极大地减少了因部署环境不同带来的差异&#xff0c;实现了一次构建、随处运行的效果。此外&#xff0c;容器化还具有版本管理、快速启动、持续集成等优点。今天&#xff0c;我们将介绍如何在…
阅读更多...
【linux】运维-基础知识-认知hahoop周边

【linux】运维-基础知识-认知hahoop周边

1. HDFS HDFS&#xff08;Hadoop Distributed File System&#xff09;–Hadoop分布式文件存储系统 源自于Google的GFS论文&#xff0c;HDFS是GFS的克隆版 HDFS是Hadoop中数据存储和管理的基础 他是一个高容错的系统&#xff0c;能够自动解决硬件故障&#xff0c;eg&#xff1a…
阅读更多...
解读 | 上海房地产政策松绑，售楼电话被“打爆”

解读 | 上海房地产政策松绑，售楼电话被“打爆”

图片来源千图网 自5月27日晚间上海发布房地产政策松绑消息以来&#xff0c;城市楼市气氛仿佛被一股暖流席卷&#xff0c;售楼电话几乎在一夜之间被“打爆”。这一次调整的政策涉及到多个方面&#xff0c;包括首套房首付比例的下调、二套房首付比例的调整、房贷利率的优惠等&am…
阅读更多...
JAVA：Random详解

JAVA：Random详解

Java中的java.util.Random类用于生成伪随机数。它提供了多种方法来生成不同类型的随机数&#xff0c;包括整数、浮点数和布尔值。以下是对Random类及其主要方法的详细介绍 一、生成随机数 创建一个Random对象&#xff0c;可以使用以下两种方式&#xff1a; 无参构造函数&…
阅读更多...
地图下钻，双击返回上一级

地图下钻，双击返回上一级

介绍&#xff1a; 看了好多地图下钻的案例&#xff0c;要么json文件不全胡&#xff0c;要么返回功能不全胡&#xff0c;有的返回是直接写死&#xff0c;返回到首页&#xff0c;我这个小案例是使用地理小工具的数据&#xff0c;本案例可以逐步一级一级的返回&#xff0c;地图的其…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023