【贪心算法】C++ 解决算法题：买卖股票 / K次取反 / 按身高排序 / 优势洗牌

1. 前言

1.1 贪心算法介绍

贪心算法（Greedy Algorithm）是一种在每一步选择中都采取当前状态下最优决策的算法。贪心算法通常用来解决最优化问题，其核心思想是通过局部最优解逐步推导出全局最优解。

在贪心算法中，我们并不总是考虑到未来可能发生的情况，而是只关注当前的最优选择。这种贪心选择性质使得贪心算法特别适合解决那些具有最优子结构性质的问题，即局部最优解能够推导出全局最优解的问题。

贪心算法的基本思路可以总结为以下几步：

确定问题的最优子结构：问题的最优解可以通过子问题的最优解逐步推导得到。
构造贪心选择：在每一步都做出当前状态下的最优选择，即局部最优解。
证明贪心选择性质：证明每一步的贪心选择都是最优的，能够推导出全局最优解。

需要注意的是，贪心算法并不适用于所有的问题，因为并非所有问题都具有最优子结构性质。在某些情况下，贪心算法得到的结果可能并不是全局最优解，而只是一个较好的解。因此，在应用贪心算法时，需要仔细分析问题的特性，以确定贪心算法是否适用于该问题。

下面会介绍一些用贪心解决的算法题：

2. 算法题

2.1_买卖股票的最佳时机

分析：

买卖股票类的问题首先有一个通用解法，就是动态规划（之前有写），这里用贪心解：
题目要求最多只能进行一次交易，因此我们可以利用循环解题

思路：

创建两个变量，ret负责记录统计过的当前最大利润，以及一个minPrev用于记录最小的买入价格
通过遍历数组，每次对两变量进行更新，最后的ret就是结果

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int ret = 0;
        for(int i = 0, minPrev = INT_MAX; i < prices.size(); ++i)
        {
            ret = max(ret, prices[i] - minPrev); // 更新结果
            minPrev = min(minPrev, prices[i]);
        }

        return ret;
    }
};

2.2_买卖股票的最佳时机II

分析：

本题与上一题的区别在于：上一题只有一次交易机会，本题可以多次交易，但是不能同时进行多笔交易，必须保证当前未持股时才能买入。

思路：

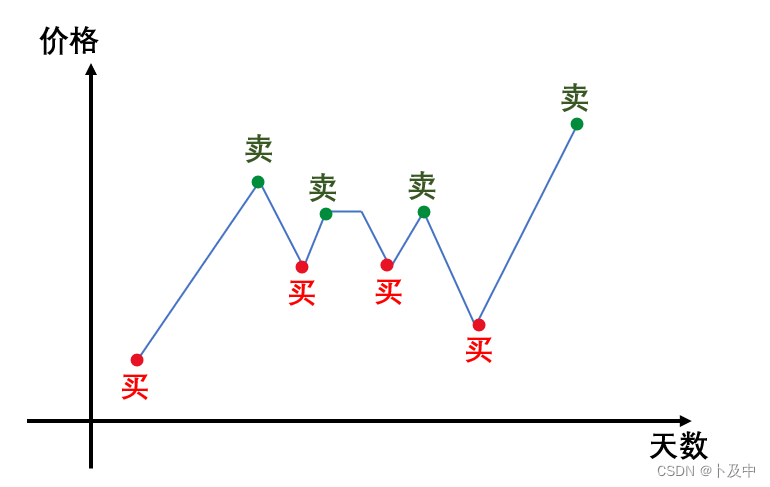
我们只要保证每次做到低进高出即可，即在递增起点买入，终点卖出；
此时有两种解决方法：
- ① 以天数为指标：遍历数组，只要出现递增，那么就将这段递增的值加入到结果ret中
- ② 利用双指针：本质是一样的，int i遍历数组，当找到一处递增时，用指针j将该递增区间统计，当走出递增时，将i和j间的距离就是这一段的递增值（利润）

代码：

利用天数：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 利用天计算
        int ret = 0, n = prices.size();
        for(int i = 1; i < n; ++i)
        {
            if(prices[i] > prices[i-1])
                ret += prices[i] - prices[i-1];
        }

        return ret;
    }
};

利用双指针：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 利用双指针
        int ret = 0, n = prices.size();
        for(int i = 0; i < n; ++i)
        {
            int j = i;
            while(j + 1 < n && prices[j+1] > prices[j])
                j++;
            ret += prices[j] - prices[i];
            i = j; // 更新i到j+1
        }

        return ret;
    }
};

2.3_K次取反后最大化的数组和

分析：

题目要求找到对整数数组nums的元素进行k次取反操作后的最大和，自然要先对负数取反，其次再对罪小的正数进行取反（贪心）

思路：

首先统计负数的个数，先将可以反转的负从最小的进行开始反转，如果所有负数均反转，且仍k>0
此时从小到大反转正数
（这个过程也可以通过一个priority_queue来完成）

代码：

class Solution {
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        int n = nums.size(), minElem = INT_MAX;
        int m = 0;
        for(auto x : nums) // 统计负数个数m
        {
            if(x < 0) ++m;
            minElem = min(minElem, abs(x)); // 找数组中绝对值最小的数
        }

        int ret = 0;
        if(m > k)
        {
            sort(nums.begin(), nums.end());
            // 将前k小的负数转正，并统计到ret
            for(int i = 0; i < k; ++i)
                ret += abs(nums[i]);

            for(int i = k; i < n; ++i)
                ret += nums[i];
        }
        else // m == k: 将所有负数转正
        {
            // m < k:
            // 先将所有负数转正；后根据k-m的奇偶性进行编写
            for(auto x : nums)
                ret += abs(x);

            if((k - m) % 2) // 奇数 // 将当前数组的绝对值最小逆号
                ret -= minElem * 2;
        }

        return ret;
    }
};

2.4_按身高排序

分析：

本质就是根据数组2的数据对数组1进行排序，可以利用vector 以及 pair<type, type> 二元组来完成；也可以创建一个下标数组，根据身高对下标数组进行排序，最后直接输出names[index[i]]；

思路：

① 创建一个vector<pair<int, string>> people，再将身高信息和姓名信息存放到该people进行降序排序
② 创建并初始化一个下标映射的数组index，排序index（利用lambda表达式）根据身高信息逆序排序，最后返回姓名names[index[i]]

代码：

利用二元组：

class Solution {
public:
    vector<string> sortPeople(vector<string>& names, vector<int>& heights) {
        // 利用二元组
        int n = names.size();
        vector<pair<int, string>> people;
        for (int i = 0; i < n; ++i) {
            people.push_back(make_pair(heights[i], names[i]));
        }

        // 根据身高降序
        sort(people.rbegin(), people.rend());

        // 提取结果
        vector<string> ret;
        for (const auto& p : people) {
            ret.push_back(p.second);
        }
        return ret;
    }
};

利用下标数组：

class Solution {
public:
    vector<string> sortPeople(vector<string>& names, vector<int>& heights) {
        // 根据身高对下标进行排序: 
        // 创建下标数组
        int n = heights.size();
        vector<int> index(n);
        for(int i = 0; i < n; ++i)
            index[i] = i;

        // 排序数组
        sort(index.begin(), index.end(), [&](const int i, const int j){
            return heights[i] > heights[j];
        });

        vector<string> ret;
        // 提取结果到数组
        for(int i = 0; i < n; ++i)
        {
            ret.push_back(names[index[i]]);
        }
        return ret;
    }
};

2.5_优势洗牌

分析：

要使优势最大，则应该尽量使用较小的大值（在nums1中找大于nums2[i]的最小值），类似田忌赛马的排列规则；

思路：

首先对nums1进行排序（便于找大于nums2[i]的最小值），由于要根据nums2更改nums1，所以不能排序nums2，创建一个下标数组并根据nums2进行排序，就可以利用index按大小顺序访问nums2的元素
创建ret，用于存放nums1改变后的位置
遍历nums1，此时的思路就是田忌赛马的思路，对于当前元素（nums1未匹配的最小元素）：
- 如果大于nums2[index2[left]]（当前最小元素），就直接匹配该元素
- 如果小于nums2[index2[left]]，那就匹配nums2的最大的元素

代码：

class Solution {
public:
    vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {
        // 1. 排序数组
        int n = nums1.size();
        sort(nums1.begin(), nums1.end());
        // 1.5 创建下标数组
        vector<int> index2(n);
        for(int i = 0; i < n; ++i)
            index2[i] = i;
        sort(index2.begin(), index2.end(), [&](const int i, const int j){
            return nums2[i] < nums2[j]; 
        });

        // 2. 田忌赛马: 如果当前比得过，则插入当前位置
        // 如果比不过，则匹配对方最大的
        int left = 0, right = n-1;
        vector<int> ret(n);
        for(auto x : nums1)
        {
            if(x > nums2[index2[left]]) ret[index2[left++]] = x;
            else ret[index2[right--]] = x;
        }

        return ret;
    }
};