思路:
这题和之前做的不大一样,之前的动态规划转化成背包问题一般都是求能放入的最大重量,这个是求组合数。
求组合数的状态转移方程之前在1和0提到过:
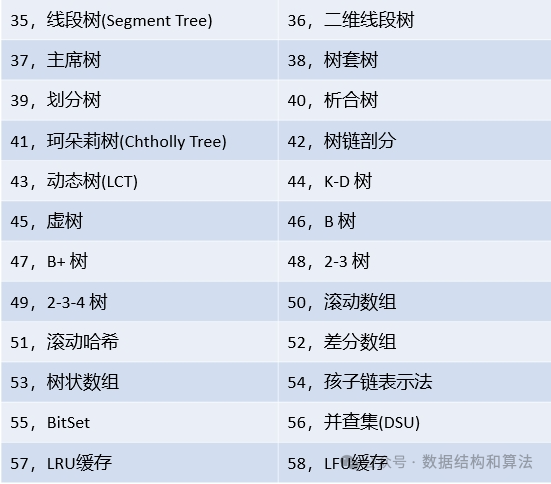
dp[j]+=dp[j-nums[]i];
这里重点分析一下遍历顺序:
这段代码里面是先遍历了物品在遍历背包容量。
在完全背包问题里面,如果是求最大重量的话,那么这两个遍历顺序是无所谓的。但是这里求的是组合数,因此遍历顺序会影响求解。
首先区分一下组合数和排列数:
组合数内部的顺序不影响答案,排序数内部的数字的顺序也可以构成不同答案。
那么对于这个二重循环:
如果先遍历物品,可以理解为把每个物品分别放到不同容量的背包里面试试,看看能不能装下。这里其实放入的顺序已经定了
如果先遍历背包容量,可以看作是对于每一种背包容量,依次把每个物品放进去试试,而因为当前背包容量与之前背包的状态有关,那么这个步骤我觉得可以看作就是对数的一个排列,顺序不同也会影响到结果
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int>dp(6000,0);
dp[0]=1;
for(int i=0;i<coins.size();i++){
for(int j=0;j<=amount;j++){
if(j>=coins[i])
dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
};











![[ C++ ] 类和对象( 下 )](https://img-blog.csdnimg.cn/direct/5f2b3c0c463d425dadae2a0bc6442f27.png)