向量
既有大小又有方向的量叫做向量
向量的模
向量的长度
单位向量 (只表示方向不表示长度)
向量的加减运算
向量求和
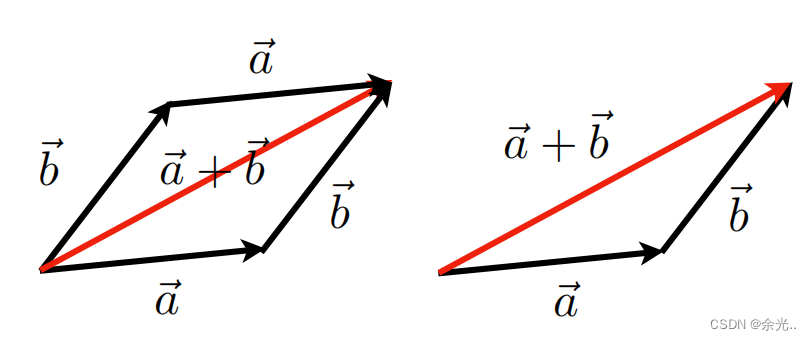
行向量与列向量的置换

图形学中竖着写
向量的长度计算
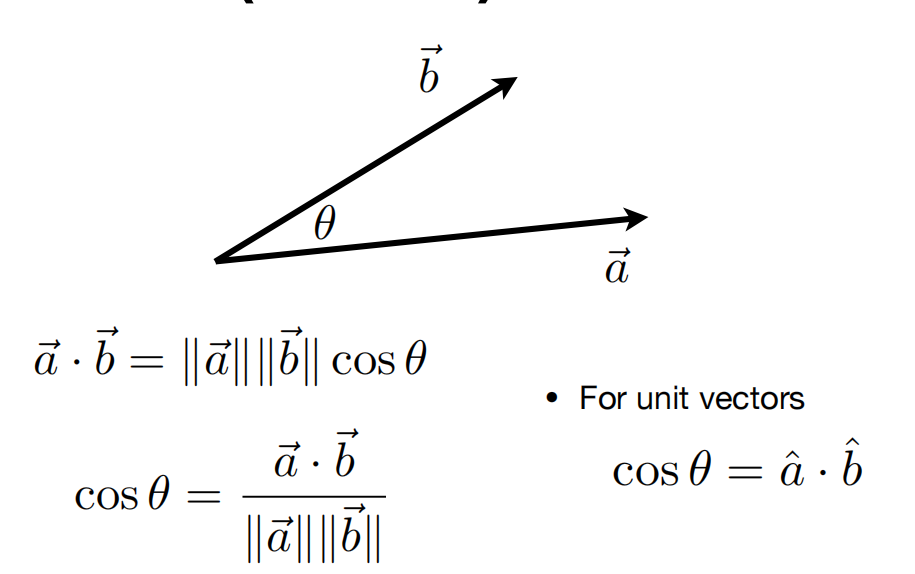
点乘(计算向量间夹角)
点乘满足的运算规律
交换律、结合律、分配律
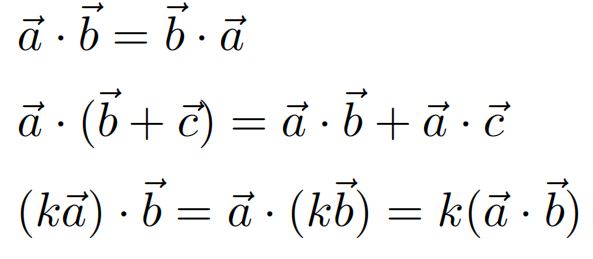
在笛卡尔坐标系下点乘的运算 (对应元素相乘)

点乘的作用
1.衡量两个方向之间的接近程度 因为一般给的两个方向都是单位向量,或者说我们应该转化为单位向量,那么点乘的值其实就是 cos(夹角),结果越接近1两向量越接近 等于0垂直 相反渐渐变成-1
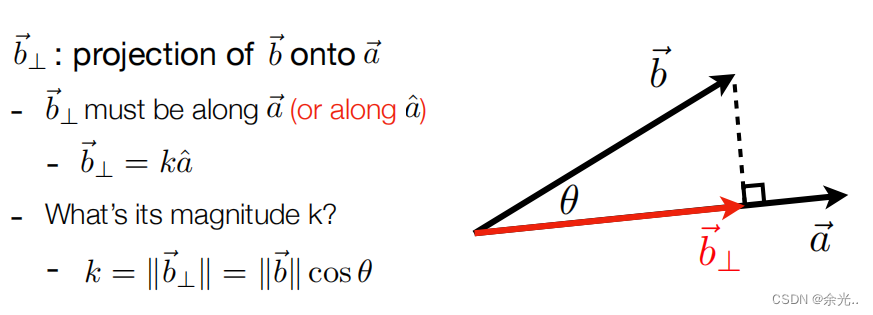
2.找到向量的投影分解向量 比如 a = xi + yj , 那么对 a 乘 i 就得到了x,乘 j 就得到了 y
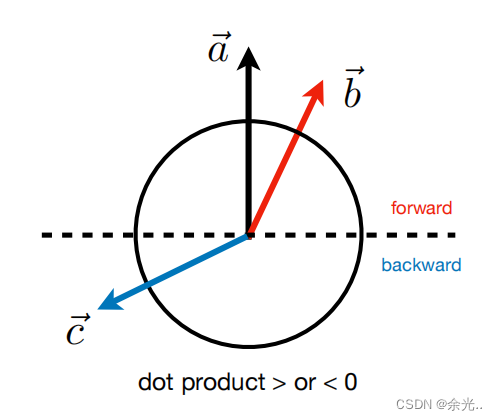
3.确定是前向还是后向 就是与一个 forward 向量做点乘,结果大于 0 说明这个方向属于前向,反之为后向 ab处在相同方向
ac处在相反方向
x向量在虚线上
叉乘(计算两向量平面的法线向量)
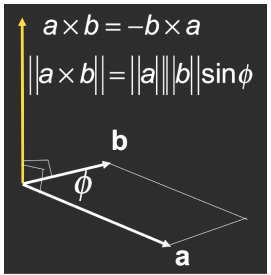
方向:右手螺旋定则
正交坐标系 两坐标轴的点乘为0,叉乘为第三个坐标轴
- 向量的叉乘不满足交换律
- 向量叉乘自己结果为0
- 满足分配律和结合律
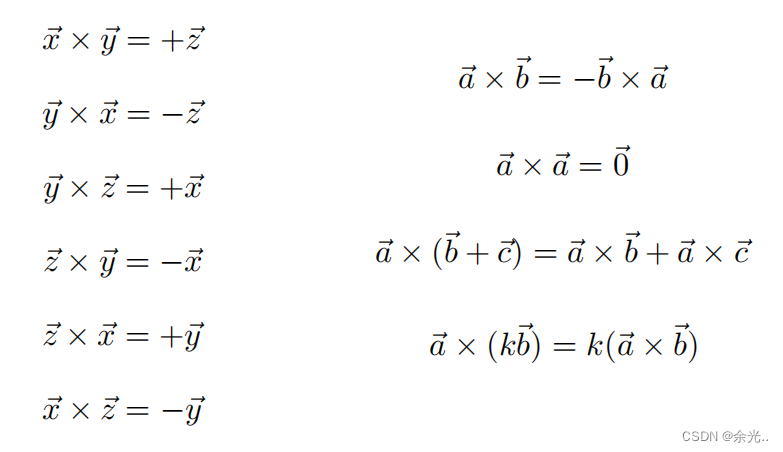
叉乘的大小可以写为矩阵形式

叉乘的作用
1.判定左与右
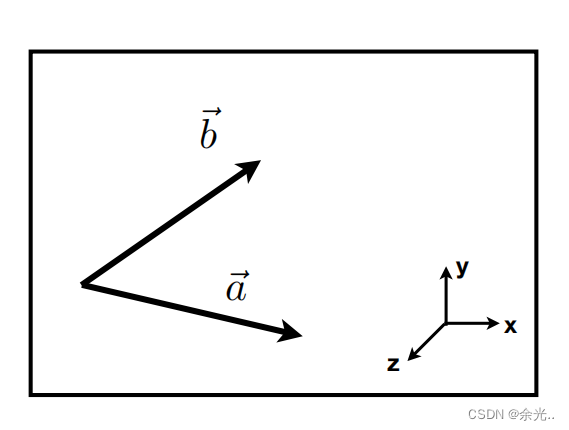
该平面为xy平面,右手螺旋定则可得z的方向。
在
的左侧
在
的右侧
2.判定内与外
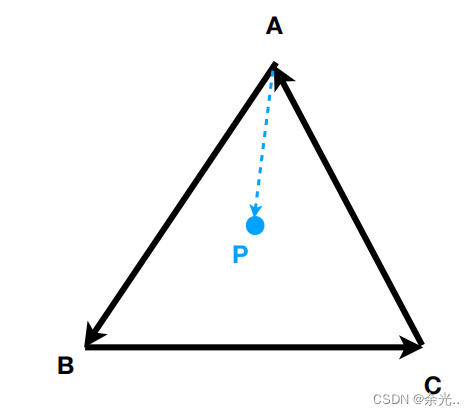
如果P点都在向量AB, BC, CA的同一侧(左侧或者右侧),那么P在三角形的内部。
所以P点在三角形内部需要同时满足三组判断
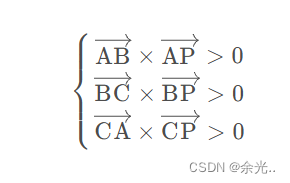
或者
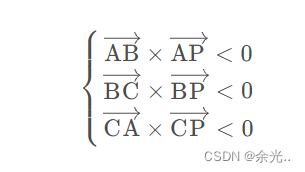
(注:这里规定垂直纸面向外为正,实际上叉乘得到的是向量。)
光栅化一个三角形时,要判断像素点在三角形的内部还是外部,就按照这种方法判断。
3.建立直角坐标系
规定直角坐标系的三个基满足
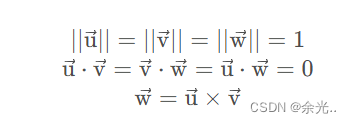
就认为u v w可组成一个直角坐标系
任何一个向量可以表示为
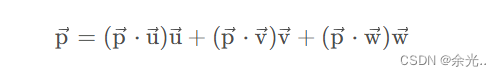
矩阵
矩阵的乘积
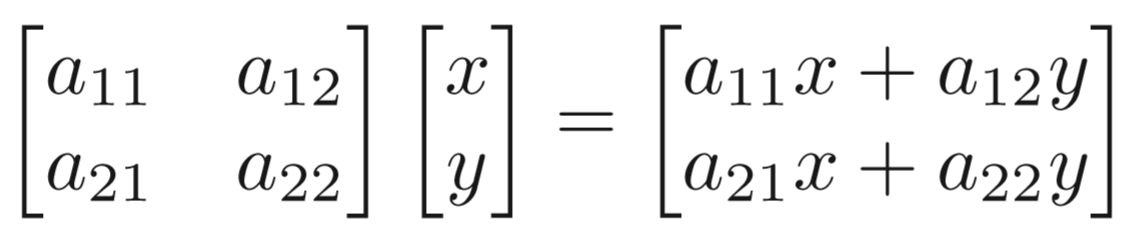
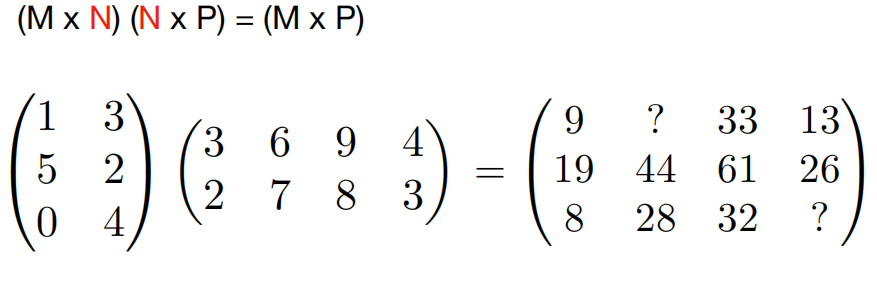
矩阵的加减运算
没有交换律,有结合律和分配律
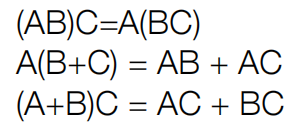
求镜像矩阵
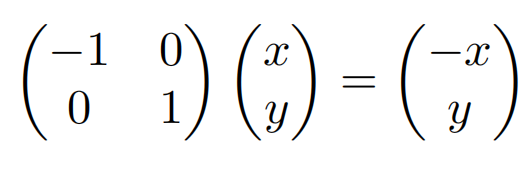
矩阵的转置
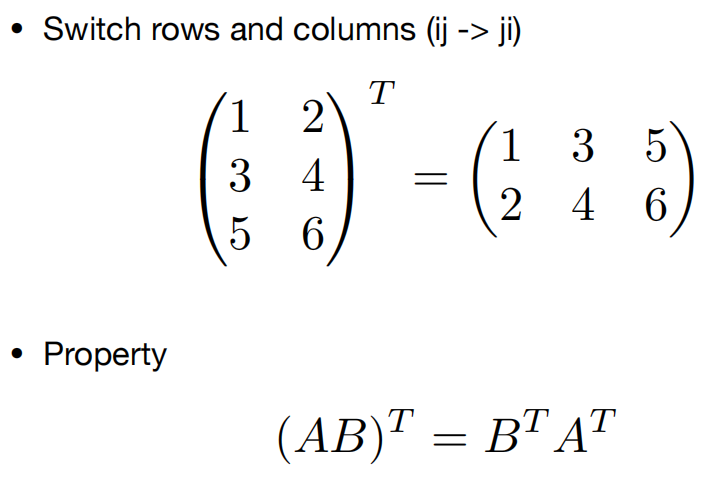
乘两个矩阵再转置,需要先对后一个矩阵转置再转置前一个再乘积
单位矩阵

矩阵的逆
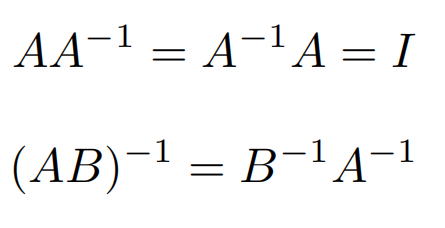
向量的点乘和叉乘写成矩阵形式
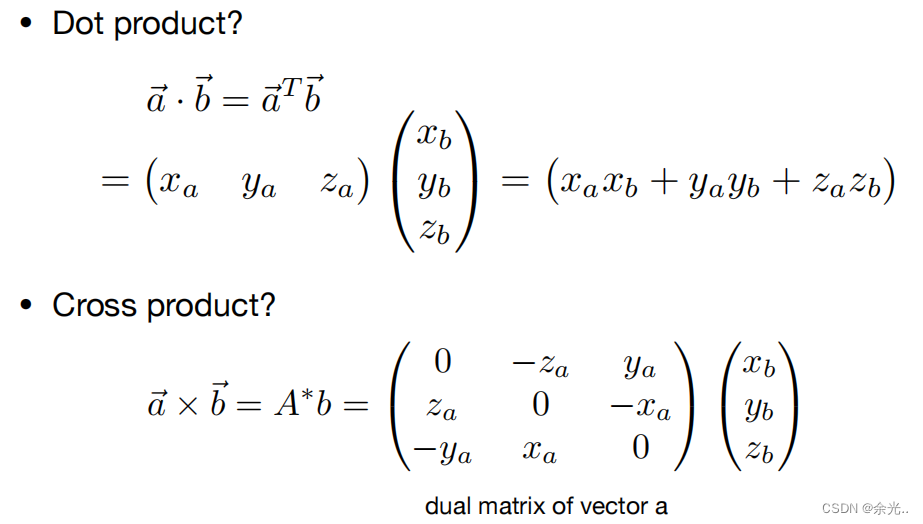
![[ C++ ] 类和对象( 下 )](https://img-blog.csdnimg.cn/direct/5f2b3c0c463d425dadae2a0bc6442f27.png)