1. 机器模型 (Machine Model)

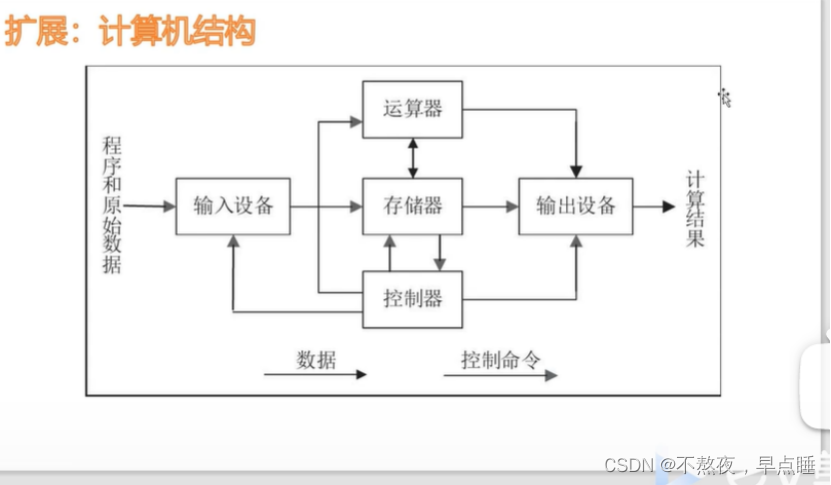
计算机的基本工作就是进行运算，那么计算就需要有用来处理计算方法的处理单元和提供或保存数值的存储单元。一般将用来处理计算方法的处理单元称为 算术逻辑单元 (ALU--Arithmetic Logic Unit)。在一个计算过程中可能会是这样的一个流程，从存储单元中取出一些数据，放进 ALU 中进行计算，然后将计算结果保存到存储单元中。

那么完成这个计算流程的机器模型是如何利用存储单元和算术逻辑单元构建起来的？该如何访问存储器？机器模型该允许什么样的指令和操作？操作数怎么获取从哪来？结果又该放在哪？

⭐
首先明确一点，机器模型不是指令集架构，上篇文章《【计算机体系结构-01】指令集体系结构、微体系结构简介》已经说明了，指令集架构是为软件编程提供的一种规范，它是关于计算和操作指令如何封装制定的一套标准，而 机器模型则是一种更加基础的理论，是构建出存储器和 ALU 的物理结构，从而确定数据如何移动，又如何从 ALU 移动到存储器。

2. 几种简单的机器模型

2.1. 栈基架构 (Stack-Based Architecture)

不管你信不信，在一个处理器中是可以没有寄存器的（寄存器不是必要的）。OK，来看一个历史上实际搭建过的处理器，它的结构非常简单。

那么可以看图片中的这种机器模型，利用栈结构存储，而栈只是一个存储器，并非寄存器。栈的结构相信大家已经很清楚，数据会遵循先入后出的顺序入栈、出栈。这个 机器模型的工作流程很简单，只需要从栈顶开始取两个元素，通过 ALU 计算，然后将结果保存栈顶。

2.2. 累加器架构 (Accumluator Architecture)

下面是一个累加器的结构。

累加器，顾名思义会对一个数值不停的做加法，而得到的结果最终也只会有一个，操作数只有一个，因此在处理器中只会有一个寄存器，所有的计算都是自动的或不可见的。同时还可以提供给累加器另外一个操作数，即除了寄存器中的操作数还提供一个来自存储器 (Memory) 的操作数，此时则需要给该操作数命名。

2.3. 寄存器-存储器架构 (Register-Memory Architrecture)

根据上面累加器的两个参数方案那么很容易想到上图这种架构，寄存器-存储器架构，即一个源操作数来自于存储器，该操作数需要命名，而另一个操作数可以来自于寄存器（不需要命名），然后，还可以有一个目的存储（可选），用于保存计算结果的存储位置，同样需要命名才可以。那么这种结构一个操作最多需要有两个命名的操作数。

2.4. 寄存器-寄存器架构 (Register-Register Architecture)

那么寄存器-寄存器架构，两个操作数均来自于处理器中的寄存器，同时两者均需被命名，当需要有目的存储时，还需要为目的存储操作数命名。

2.5. 以上几种架构的比较

这四种架构，需要被命名的操作数数目分别为 0、1、2或3、2或3，相信通过上文你已经清楚了，后面两种架构为什么是 2或3，因为有时候数据计算结果的保存目的地会隐式的确定无需命名，当需要明确指出时，那么就会多一个命名操作数。

例如，X86 架构中的第一个操作数总是作为结果的保存位置，因此它会少命名一个操作数。例如 MIPS、RISC 架构则需要将三个操作数全部命名。

3. 栈基架构 (Stack-Based Architecture)

3.1. 栈基架构机器模型工作原理

栈基架构虽然是个很老的架构模型，但是很经典。过去的 Burrough's 5000 (B5000) 机器就是使用的栈基架构（1960年），近一点的 Java 虚拟机实际上也是利用栈结构实现。

用一个例子🌰来说明栈基架构机器模型的工作原理，来看上图这个计算表达式，首先用 a 加上 b * c，然后整个括号的计算结果除以 a 加上 d * c 再减去 e 的运算结果才得到最终的表达式结果。这对于我们来说计算这个表达式很简单，但对于计算机来说就没那么直接了，甚至有点复杂。

实际上计算机会将这个表达式分解并生成一个 解析树，就上图这样。一个二叉树的结构，所有的叶子节点上是需要做计算的数，其它节点则是运算符。开始先由 b 乘以 c 加上 a，用这个结果除以另一边的子表达式。整个二叉树用顺序结构保存即为计算机应该要做的操作表达式，像下面这样。

如果现在使用的是栈基架构的机器模型，那么就意味着会有一个求值栈，首先 push a 到栈中，接着 push b 到栈中、push c 到栈中，当遇到运算符，拿栈顶的两个元素做对应的运算，再保存到栈中，依次类推就会得到下面这样的栈操作流程。

通过这样的栈操作流程，就可以把左边的子表达式结果计算出来，依照该方法继续姐可以计算出整个表达式的结果。你会发现计算机在计算这样长的表达式，实际上可以在一个很小的栈中完成对整个表达式的计算，并且有一个好处是，完全不需要对任何一个操作数命名（因为操作数是固定的，总是拿栈顶的两个元素作运算）。因此这个机器模型可以让你跑任何现实的程序。

⭐
需要注意的一点是，栈是处理器状态的一部分，并且很多时候在指令集体系架构的角度来看栈是无限大的。但在实际上，计算机中的栈是有限长的，因为在计算机中无论如何都不可能出现一个无限长且真实存在的栈。它只是在概念上是无限的，因此你需要保证不能发生栈溢出（内存溢出、主存储器溢出）。 例如，上面例子中的表达式如果是很长，或者产生的解析树太深，都会导致栈溢出的可能。

3.2. 栈基架构的设计和优化（求值栈）

🤕基础设计：
假如现在有一个指令集架构的微架构实现是基于栈基架构的，由于求值栈在进行计算时总是需要两个操作数，那么就将求值栈中的顶部的两个元素的地址是保存在寄存器中，而其余的则保存在主存中（包含溢出的元素）。每一次入栈操作都会产生一次内存引用，每一次出栈操作也会有一次内存引用（出栈会将栈中的元素返回到主存中）。而且更重要的是，当发生栈溢出后，将会增加额外的内存引用，因为在做栈操作时需要将主存的数据先拿出来。显然，这样的结构让操作产生的步骤非常的多（内存引用）。

🤪优化设计：
那么站在微系体系架构优化的角度考虑，将栈中的 N 个元素全部直接保存在寄存器中（栈中的所有元素 N 小于或等于可用的寄存器数），这样每次执行 push 和 pop 操作时就不必执行内存引用，就只有当发生栈溢出时才需要增加一步内存引用操作。

Okay，用优化后的栈来计算一下，继续再用上面的例子，现在给出限制条件，限制栈的大小为 2，即最多只能放两个元素，超过则会发生溢出。

先来看这个例子都会做什么，首先 push 了三次元素进栈，然后对顶部的两个元素做乘法，然后再做加法，之后再三次 push 操作，栈顶两个元素相乘，用结果加上 a，接着 push e，用上一次结果减去 e，再将栈顶两个元素做除法完成计算。

但是栈中只能存放两个元素，那么来看看在栈操作中具体会发生什么事情，

• 第一步 push a，这时候时空栈，没问题，直接进，非空非满栈；
• 第二步，接着 push b，也 OK，此时为满栈；
• 第三步，当 push c 的时候，发现栈已经满了，这个时候还想要再 push，那就会发生 栈下溢 (Underflow)，此时会先将栈底元素也就是 a，保存到主存中 (Main Memory)，该操作会发生一次内存引用，图中的 ss(a) 表示将 a store 到主存中，R0 寄存器的值改变为 a 的主存地址（这便发生额外的一次内存引用），然后将 c 压入栈顶。
• 第四步，将栈顶的两个元素做乘法运算，将结果 b * c 保存到 R1，栈元素减一，同时从 a 的主存地址获取 (fetche) a（发生内存引用）也就是图中的 sf(a)，将 a 保存到 R0 中，此时栈中有两个元素，栈顶是 R1 = b * c，满栈；
• 第五步，将栈顶的两个元素做加法运算，将结果 a + b * c 入栈保存到 R0，栈元素减一，此时栈中只有一个元素即为栈顶元素 R0 = a + b * c，非空非满栈；
• 第六步，push a，进栈，没问题，R1 = a，此时为满栈，栈顶元素为 a；
• 第七步，push d 进栈，发生 underflow，将栈底元素保存到主存发生一次内存引用 (ss(a + b * c))，R0 保存 a + b * c 的存储地址，此时栈顶元素为 R2 = d，满栈；
• 第八步，push c 进栈，发生 underflow，将栈底元素保存到主存，发生一次内存引用 (ss(a))，此时栈顶元素为 R3 = c，满栈；
• 第九步，将栈顶的两个元素做乘法运算，将结果 d + c 保存到 R2，栈元素减一，同时从 a 的主存地址获取 (fetche) a（发生内存引用）也就是图中的 sf(a)，将 a 保存到 R1 中，此时栈中有两个元素，栈顶是 R2 = b * c，满栈；
• 第十步，将栈顶的两个元素做加法运算，将结果 a + d * c 保存到 R1，栈元素减一，同时从 a + b * c 的主存地址获取 (fetche) a + b * c 的值（发生内存引用）也就是图中的 sf(a + b * c)，将 a + b * c 保存到 R0 中，此时栈中有两个元素，栈顶是 R1 = a + d * c，满栈；
• 第十一步，push e 入栈操作，发生 underflow，将栈底元素保存到主存发生一次内存引用 (ss(a + b * c))，R0 保存 a + b * c 的存储地址，此时栈顶元素为 R2 = e，满栈；
• 第十二步，将栈顶的两个元素做减法运算，将计算结果 a + d * c - e 保存到 R1，栈元素减一，同时从 R0 保存的主存地址拿出 a + b * c 的值保存进 R0，此时为满栈，栈顶元素 R1 = a + d * c - e；
• 第十三步，将栈顶的两个元素做除法运算，将计算结果 (a + b * c) / (a + d * c - e) 用 R0 保存，栈元素减一。

统计一下，利用这个求值栈计算过程中间接性的做了 4 次 store 操作和 4 次 fetche 操作，也就是说使用该结构栈在正常的流程中额外的增加了 8 次访存操作。

我们改变一下栈大小会发生什么，将栈的大小增加为 4，那么它的执行流程将会是下面这样。

哇呜，一气呵成，中间没有发生内存引用，Good。因为计算该表达式最多的情况下会一次性有 4 个元素在栈中，那么栈的大小只要满足，就不会发生栈溢出的情况，也就不会有内存引用这样额外的访存操作了。

3.3. 栈基架构小结

通过上面的几个例子，相信各位已经清楚了栈基架构的机器模型。看起来他们是可以成功的完成计算任务，但是有一个明显的问题不知道机智的你有没有发现。第一步的时候 push a，将 a 入栈，接着后面又有一次 push a，push c 同样是，我们再做重复多余的工作欸！！栈基机器模型的架构很简单，指令很密集，但这对于机器性能不算是好事，因为使用该模型将意味着要面临多次的重新读取。

如果使用指令集架构，如 MIPS，那么将会有 32 个通用寄存器，可以在任何指令中为任何一个寄存器命名。那么这时候，当你已经 load 了 a、b、c、d、e 数值到寄存器空间中一次了，那么之后所有关于这几个数的操作时都无需重新 load。事实上这个问题时由指令集解决的，并不是基础机器模型的问题，也不是微架构要解决的问题。

4. 对比几种简单的机器模型

上文已经介绍了这四种机器模型，Stack-Based、Accumulator、Register-Memory、Register-Register。现在用一个简单的计算 C = A + B，分别使用这四个机器模型，看看会有什么不同。

• Stack-Based Architecture

栈基架构的机器模型的工作过程就是，Push A，将 A 的值入栈，Push B，将 B的值入栈，用栈顶两个元素做 Add 操作，然后将结果 Pop 到 C 中保存。

• Accumulator Architecture

累加器的机器模型工作过程为，Load A，Add B 即 A + B，然后将结果 Store 到 C 中。

• Register-Memory Architecture

寄存器-存储器架构机器模型的工作过程，Load R1, A、Add R3, R1, B，将 B 的值与 R1 保存的值相加，将结果保存到 R3 中，再将 R3 的值 Store 到 C 中。

• Register-Register Architecture

寄存器-寄存器架构机器模型的工作过程为，Load R1, A、Load R2, B，执行 Add，将 R1 和 R2 保存的值相加，并将结果保存到 R3 中，再将 R3 的值 Store 到 C 中，完成计算。

相比前两个架构，后两个架构在使用 A、B 之前需要先 Load，计算完后还需要 Store，看起来似乎不够高效，没有前面两个模型简洁，但是当之后需要重复性的使用 A、B 的值进行计算的话，那么后两个架构，将不需要再次 Load，而可以直接使用，而前两个架构则需要重复性的执行 Push 或 Load 指令，这样看起来优势就会体现出来了。

觉得这篇文章对你有帮助的话，就留下一个赞吧*^v^*
请尊重作者，转载还请注明出处！感谢配合~
[作者]: Imagine Miracle
[版权]: 本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
[本文链接]: https://blog.csdn.net/qq_36393978/article/details/128717724