目录
离散信源信息的度量:
离散信源的信息量:
单符号离散无记忆信源:
离散无记忆信源及熵:
自信息:
信息量的定义:
信息熵的定义:
熵的性质:
离散信源的最大熵定理:
联合自信息:
条件自信息:
离散信源的联合熵:
离散信源的条件熵:
香农关于“信息”的概念:
(1)事物发展变化的因果关系是复杂的,存在其必然性也存在偶然性,事物发展变化的结果往往是不确 定的。
(2)信息—事物运动状态与存在方式的不确定性的描述。
(3)存在不确定性->需要获得信息。
(4)不确定性的消除=获得的信息。
(5)信息的多少与获得某个消息令人产生的“意外有关”。
(1) 某消息的信息量=获得该消息后不确定性的消除量。
不确定性-可能性-概率问题
信息量可用概率的某种函数来度量
(2) 不同的消息有信息量的多少的区别,因此信息的度量方应满足信息量的可加性。
信息量应该是满足可加性的概率的函数。
离散信源信息的度量:
离散信源的信息量:
离散信源统计特性的描述方法--概率场
设离散信源包含N种可能的不同符号,相应的概率场可表述为:
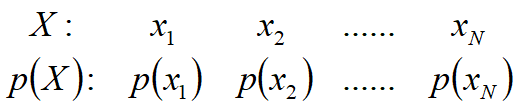
概率场应满足条件:
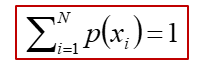

单符号离散无记忆信源:


离散无记忆信源及熵:
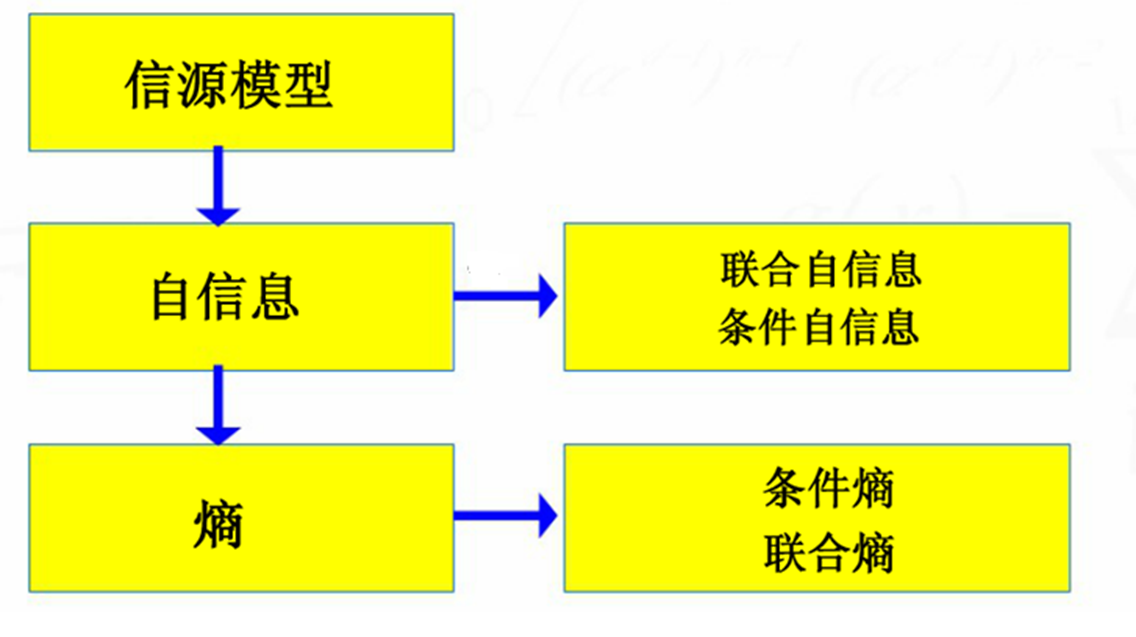
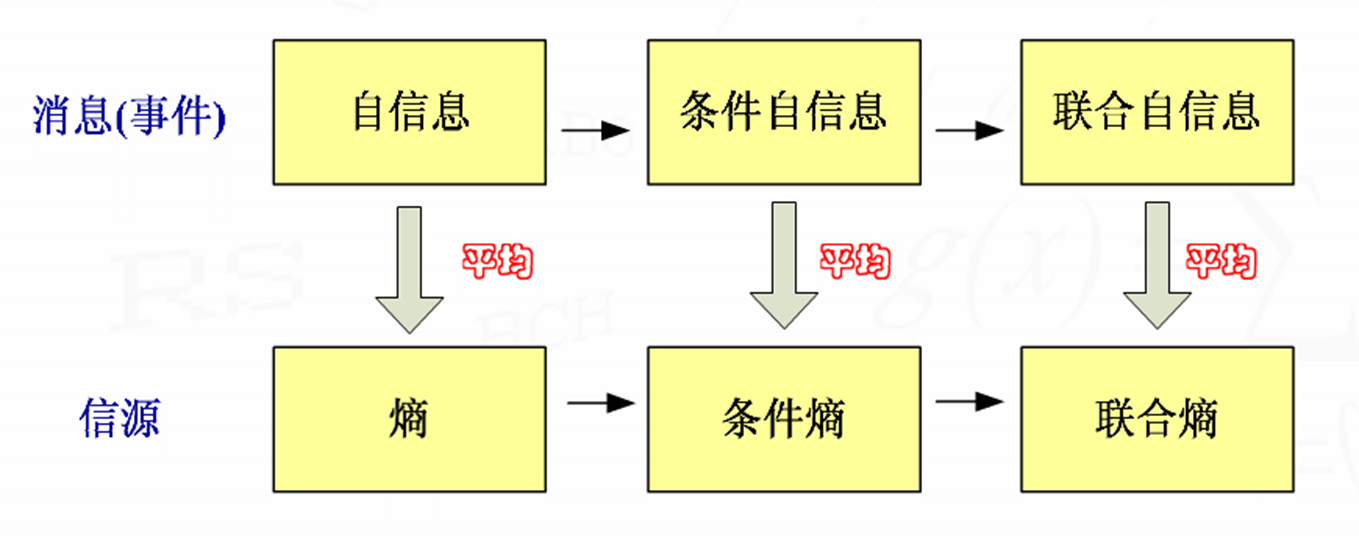
自信息:
信息:不确定性,随机性,惊讶程度
自信息:
(1)某事件发生前的不确定性的大小;
(2)某事件发生后能提供的信息量的大小。
信息量的定义:
信息量作为概率的函数,具有形式:
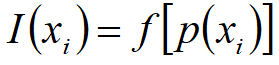
应满足条件:

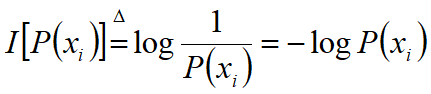
信息量的单位与对数的底有关:
log以2为底时,单位为比特:bit
log以e为底时,单位为奈特:nit
log以10为底时,单位为哈特,hart
一般在没有特别声明时均假定信息的单位为比特。

信息熵的定义:

熵的性质:
(1)表示信源输出前,信源的平均不确定性;信源输出后各个消息所能提供的平均信息量。
(2)对于一个给定的信源X,其熵H(X)是固定常数。
(3)概率为0的事件对熵有影响吗?没有影响。
(4)单位:比特/符号,奈特/符号,哈特/符号。
(5)信源中各个符号概率分布越均匀,信源熵越大。

离散信源的最大熵定理:
当离散信源X取等概分布时,其熵取最大值。
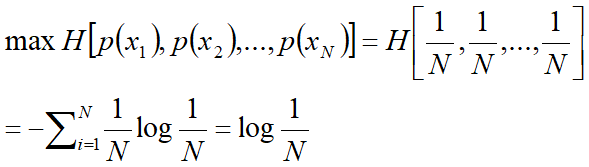
当信源取等概分布时,具有最大的不确定性

联合自信息:
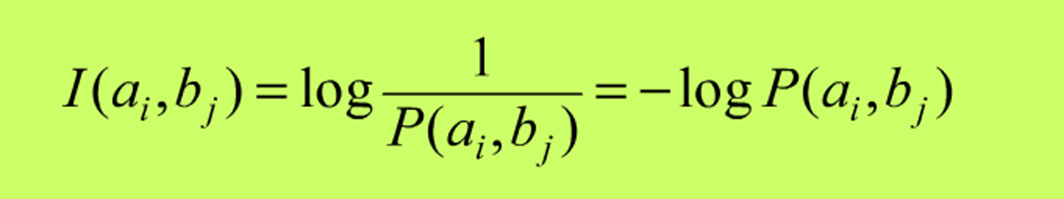

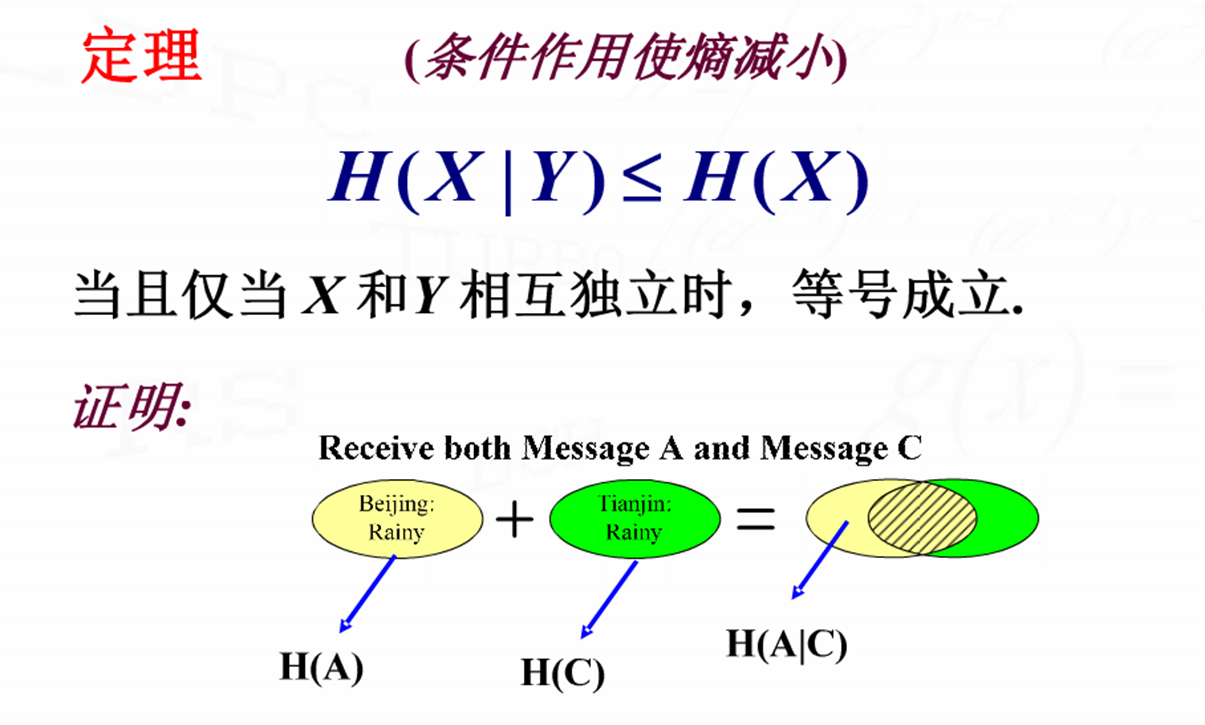
条件自信息:


离散信源的联合熵:

离散信源的条件熵: