单目相机标定实现--张正友标定法

文章目录

- 一：相机坐标系，像素平面坐标系，世界坐标系，归一化坐标系介绍
- - 1：概述
  - 公式
- 二:实现
- - 1：整体流程
  - 4：求出每张图像的单应性矩阵并用LMA优化
  - 5：求解理想无畸变情况下的摄像机的内参数和外参数
  - 6：应用最小二乘求出实际的畸变系数
- 五：总结

原文链接：http://t.csdn.cn/Qvvjv

个人笔记：
本次介绍针对于单目相机标定，实现方法：张正友标定法。

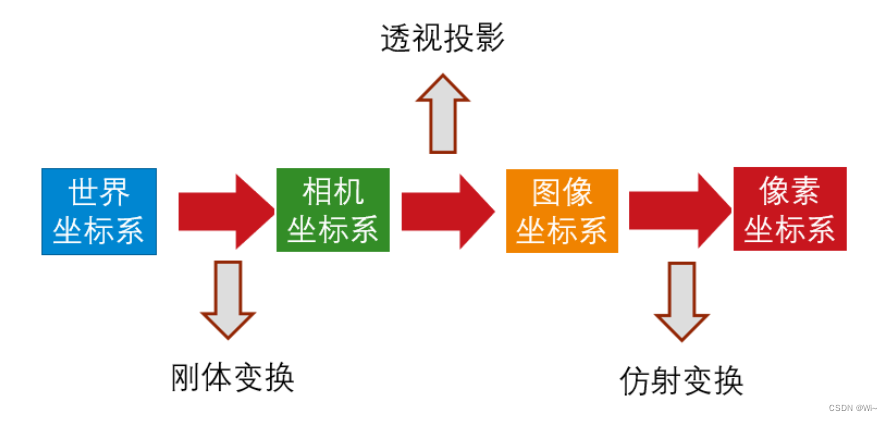
一：相机坐标系，像素平面坐标系，世界坐标系，归一化坐标系介绍

1：概述

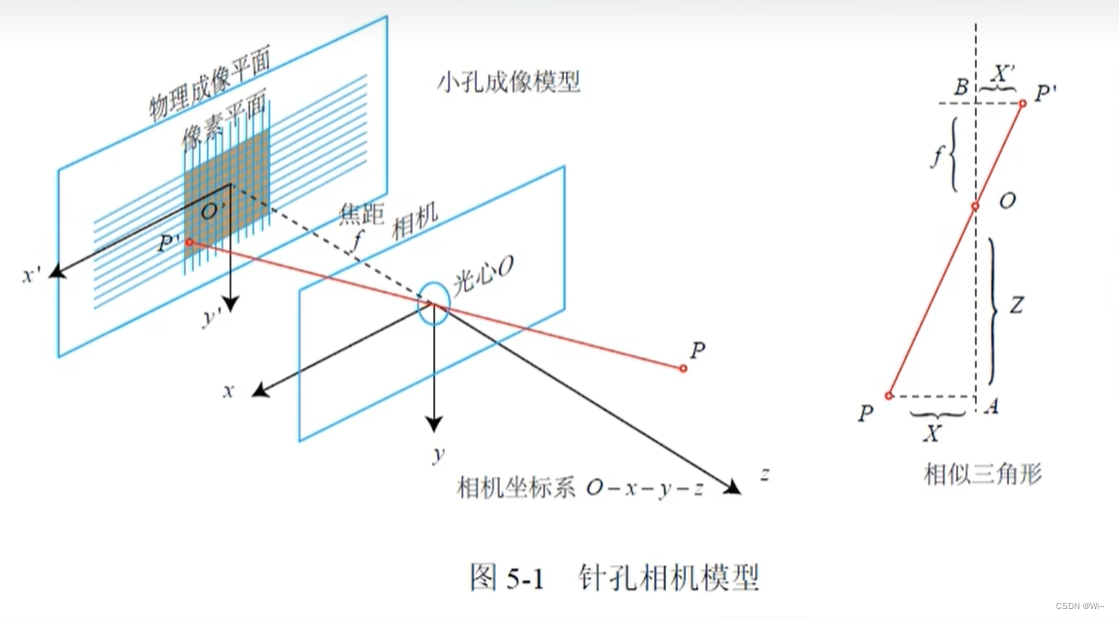
在这里插入图片描述

如图，现实世界中有一个P点和一个相机（光心），描述这个P点的空间坐标首先得有一个坐标系，那么以光心为原点O建一个坐标系，叫相机坐标系。
那么就可以在相机坐标系下，设 $P 坐标 (X, Y, Z)$ 和P的投影点 $P^{'} (x^{'}, y^{'}, z^{'})$ 。值得一提的是， $P^{'} (x^{'}, y^{'}, z^{'})$ 坐落在物理成像平面和像素平面。
物理成像平面，像素平面是二维的，他们的坐标系并不一样：
物理成像平面在 $O^{'} (x^{'}, y^{'})$ 平面上；
像素平面的原点在那个黑灰色图的左上角(图片的左上角)，横轴向右称为 $u$ 轴，纵轴向下称为 $v$ 轴。
这样就得到了 $P^{'}$ 的像素坐标 $P (u, v)$ ，称为 $P uv$ 。

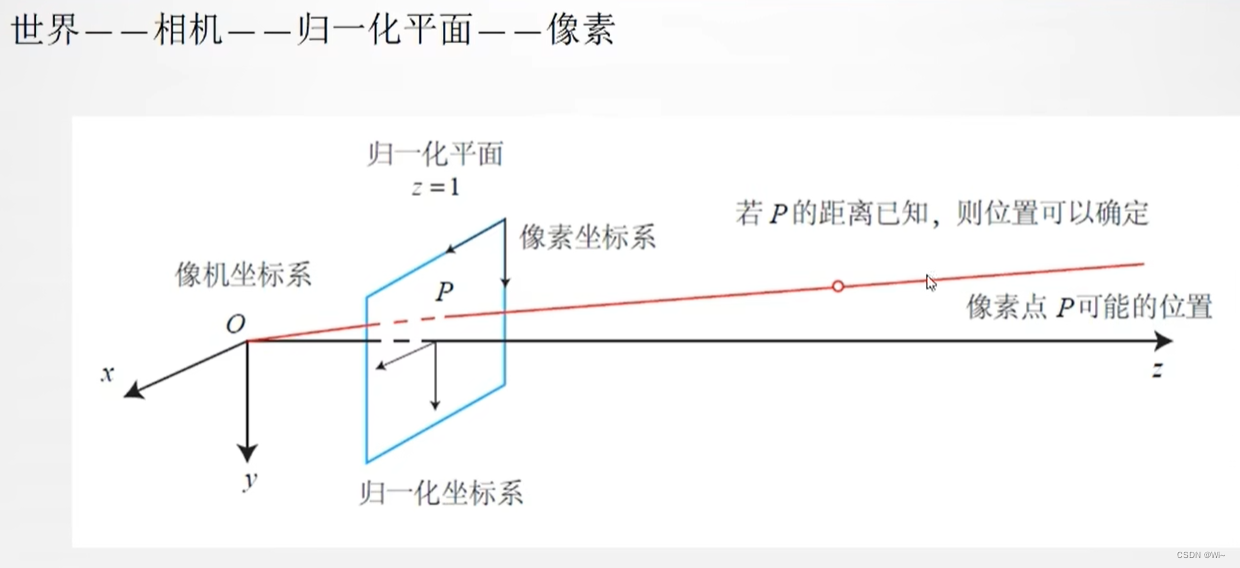在这里插入图片描述所谓的归一化的成像平面，就是将三维空间点的坐标都除以Z，在相机坐标系下，P有X, Y, Z 三个量，如果把它们投影到归一化平面 Z = 1 上，就会得到P的归一化坐标P(X/Z, Y/Z, 1)。

公式

在这里插入图片描述
$\left[\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right]->$ 物体坐标.

$\left[\begin{array}{cc} R & T \\ 0 & 1 \end{array}\right]->$ 外参

$\left[\begin{array}{cccc} \alpha & \gamma & u_{0} & 0 \\ 0 & \beta & v_{0} & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]->$ 内参

$\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]->$ 像素坐标

其中外参 $T$ 是平移向量 $t1,t2,t3)^T$ .
$R$ 旋转矩阵如下图：
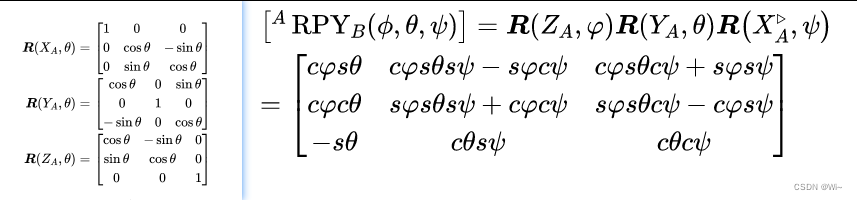
在这里插入图片描述

二:实现

1：整体流程

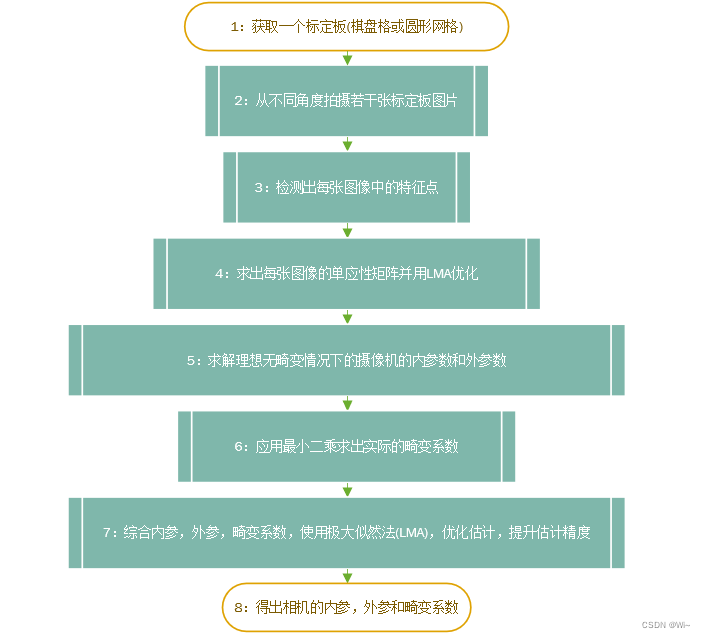
在这里插入图片描述
第1步，第2步，第3步暂不介绍了，主要介绍获取到特征点以后，优化获取参数部分。

4：求出每张图像的单应性矩阵并用LMA优化

如何计算单应性矩阵：
$\begin{array}{c} \left[\begin{array}{l} x_{b} \\ y_{b} \\ w_{b} \end{array}\right]=\left[\begin{array}{ccc} \mathrm{h}_{1} & \mathrm{~h}_{2} & \mathrm{~h}_{3} \\ \mathrm{~h}_{4} & \mathrm{~h}_{5} & \mathrm{~h}_{6} \\ \mathrm{~h}_{7} & \mathrm{~h}_{8} & \mathrm{~h}_{9} \end{array}\right]\left[\begin{array}{l} x_{a} \\ y_{a} \\ w_{a} \end{array}\right] \\\\ \frac{x_{b}}{w_{b}}=\frac{h_{1} x_{a}+\mathrm{h}_{2} y_{a}+\mathrm{h}_{3} w_{a}}{h_{7} x_{a}+\mathrm{h}_{8} y_{a}+\mathrm{h}_{9} w_{a}}=\frac{h_{1} x_{a} / w_{a}+\mathrm{h}_{2} y_{a} / w_{a}+\mathrm{h}_{3}}{h_{7} x_{a} / w_{a}+\mathrm{h}_{8} y_{a} / w_{a}+\mathrm{h}_{9}} \\ \frac{y_{b}}{w_{b}}=\frac{h_{4} x_{a}+\mathrm{h}_{5} y_{a}+\mathrm{h}_{6} w_{a}}{h_{7} x_{a}+\mathrm{h}_{8} y_{a}+\mathrm{h}_{9} w_{a}}=\frac{h_{4} x_{a} / w_{a}+\mathrm{h}_{5} y_{a} / w_{a}+\mathrm{h}_{6}}{h_{7} x_{a} / w_{a}+\mathrm{h}_{8} y_{a} / w_{a}+\mathrm{h}_{9}} \end{array}$

$\text { 令 } u_{a}=\frac{x_{a}}{w_{a}}, v_{a}=\frac{y_{a}}{w_{a}}, u_{b}=\frac{x_{b}}{w_{b}}, v_{b}=\frac{y_{b}}{w_{b}} \text {, 上式化简为 }$
$\begin{array}{l} u_{b}=\frac{h_{1} u_{a}+\mathrm{h}_{2} v_{a}+\mathrm{h}_{3}}{h_{7} u_{a}+\mathrm{h}_{8} v_{a}+\mathrm{h}_{9}} \\ v_{b}=\frac{h_{4} u_{a}+\mathrm{h}_{5} v_{a}+\mathrm{h}_{6}}{h_{7} u_{a}+\mathrm{h}_{8} v_{a}+\mathrm{h}_{9}} \end{array}$

$\begin{array}{c} h_{1} u_{a}+h_{2} v_{a}+h_{3}-h_{7} u_{a} u_{b}-h_{8} v_{a} u_{b}-h_{9} u_{b}=0 \\ h_{4} u_{a}+h_{5} v_{a}+h_{6}-h_{7} u_{a} v_{b}-h_{8} v_{a} v_{b}-h_{9} v_{b}=0 \end{array}$

$\text { 可以直接设 }\|h\|_{2}^{2}=1 \text { ，此时仍然可以固定住尺度，且有: }$
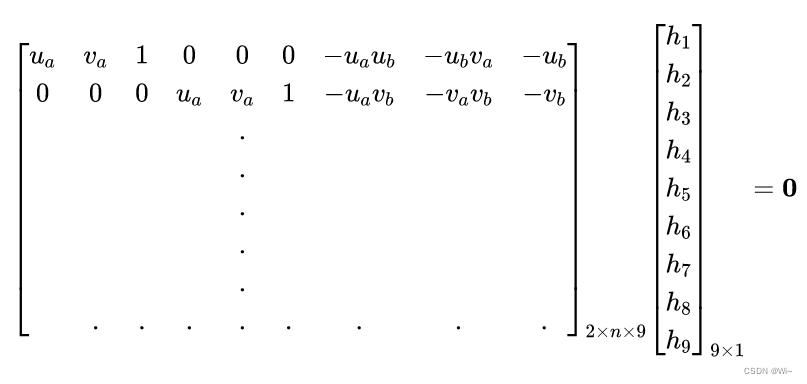
在这里插入图片描述

此时系数矩阵秩为8，有线性空间解，解的自由度为1，满足齐次性，又由于限制单位长度，有唯一解，此时仍可以通过SVD分解求解出 h，从而得到单应矩阵。

代码实现：

//获取标准差
double CameraCalibration::StdDiffer(const Eigen::VectorXd& data)
{
    //获取平均值
    double mean = data.mean();
    //std::sqrt((Σ(x-_x)²) / n)
    return std::sqrt((data.array() - mean).pow(2).sum() / data.rows());
}

// 归一化
Eigen::Matrix3d CameraCalibration::Normalization (const Eigen::MatrixXd& P)
{
    Eigen::Matrix3d T;
    double cx = P.col ( 0 ).mean();
    double cy = P.col ( 1 ).mean();

    double stdx = StdDiffer(P.col(0));
    double stdy = StdDiffer(P.col(1));;


    double sqrt_2 = std::sqrt ( 2 );
    double scalex = sqrt_2 / stdx;
    double scaley = sqrt_2 / stdy;

    T << scalex, 0, -scalex*cx,
            0, scaley, -scaley*cy,
            0, 0, 1;
    return T;
}

//获取初始矩阵H
Eigen::VectorXd CameraCalibration::GetInitialH (const Eigen::MatrixXd& srcNormal,const Eigen::MatrixXd& dstNormal )
{
    Eigen::Matrix3d realNormMat = Normalization(srcNormal);
    Eigen::Matrix3d picNormMat = Normalization(dstNormal);

    int n = srcNormal.rows();
    // 2. DLT
    Eigen::MatrixXd input ( 2*n, 9 );

    for ( int i=0; i<n; ++i )
    {
        //转换齐次坐标
        Eigen::MatrixXd singleSrcCoor(3,1),singleDstCoor(3,1);
        singleSrcCoor(0,0) = srcNormal(i,0);
        singleSrcCoor(1,0) = srcNormal(i,1);
        singleSrcCoor(2,0) = 1;
        singleDstCoor(0,0) = dstNormal(i,0);
        singleDstCoor(1,0) = dstNormal(i,1);
        singleDstCoor(2,0) = 1;


        //坐标归一化
        Eigen::MatrixXd realNorm(3,1),picNorm(3,1);
        realNorm = realNormMat * singleSrcCoor;
        picNorm = picNormMat * singleDstCoor;

        input ( 2*i, 0 ) = realNorm ( 0, 0 );
        input ( 2*i, 1 ) = realNorm ( 1, 0 );
        input ( 2*i, 2 ) = 1.;
        input ( 2*i, 3 ) = 0.;
        input ( 2*i, 4 ) = 0.;
        input ( 2*i, 5 ) = 0.;
        input ( 2*i, 6 ) = -picNorm ( 0, 0 ) * realNorm ( 0, 0 );
        input ( 2*i, 7 ) = -picNorm ( 0, 0 ) * realNorm ( 1, 0 );
        input ( 2*i, 8 ) = -picNorm ( 0, 0 );

        input ( 2*i+1, 0 ) = 0.;
        input ( 2*i+1, 1 ) = 0.;
        input ( 2*i+1, 2 ) = 0.;
        input ( 2*i+1, 3 ) = realNorm ( 0, 0 );
        input ( 2*i+1, 4 ) = realNorm ( 1, 0 );
        input ( 2*i+1, 5 ) = 1.;
        input ( 2*i+1, 6 ) = -picNorm ( 1, 0 ) * realNorm ( 0, 0 );
        input ( 2*i+1, 7 ) = -picNorm ( 1, 0 ) * realNorm ( 1, 0 );
        input ( 2*i+1, 8 ) = -picNorm ( 1, 0 );
    }

    // 3. SVD分解
    JacobiSVD<Eigen::MatrixXd> svdSolver ( input, Eigen::ComputeFullU | Eigen::ComputeFullV );
    Eigen::MatrixXd V = svdSolver.matrixV();
    Eigen::Matrix3d H = V.rightCols(1).reshaped<RowMajor>(3,3);
    //去归一化
    H = (picNormMat.inverse() * H) * realNormMat;
    H /= H(2,2);
    return H.reshaped<RowMajor>(9,1);
}

求出初始单应性矩阵 $h$ ，然后用 $L M A$ 优化，得到具有实际意义的单应性矩阵。
优化代码：


//单应性残差值向量
class HomographyResidualsVector
{
public:
    Eigen::VectorXd  operator()(const Eigen::VectorXd& parameter,const QList<Eigen::MatrixXd> &otherArgs)
    {
        Eigen::MatrixXd inValue = otherArgs.at(0);
        Eigen::MatrixXd outValue = otherArgs.at(1);
        int dataCount = inValue.rows();
        //保存残差值
        Eigen::VectorXd residual(dataCount*2) ,residualNew(dataCount*2);
        Eigen::Matrix3d HH =  parameter.reshaped<RowMajor>(3,3);
        //获取预测偏差值 r= ^y(预测值) - y(实际值)
        for(int i=0;i<dataCount;++i)
        {
            //转换齐次坐标
            Eigen::VectorXd singleRealCoor(3),U(3);
            singleRealCoor(0,0) = inValue(i,0);
            singleRealCoor(1,0) = inValue(i,1);
            singleRealCoor(2,0) = 1;
            U = HH * singleRealCoor;
            U /= U(2);

            residual(i*2) = U(0);
            residual(i*2+1) = U(1);

            residualNew(i*2) = outValue(i,0);
            residualNew(i*2+1) = outValue(i,1);
        }

        residual -= residualNew;
        return residual;
    }

};



//求单应性雅克比矩阵
class HomographyJacobi
{
    //求偏导1
    double PartialDeriv_1(const Eigen::VectorXd& parameter,int paraIndex,const Eigen::MatrixXd &inValue,int objIndex)
    {
        Eigen::VectorXd para1 = parameter;
        Eigen::VectorXd para2 = parameter;
        para1(paraIndex) -= DERIV_STEP;
        para2(paraIndex) += DERIV_STEP;

        //逻辑
        double obj1 = ((para1(0))*inValue(objIndex,0) + para1(1)*inValue(objIndex,1) + para1(2)) / (para1(6)*inValue(objIndex,0) + para1(7)*inValue(objIndex,1) + para1(8));
        double obj2 = ((para2(0))*inValue(objIndex,0) + para2(1)*inValue(objIndex,1) + para2(2)) / (para2(6)*inValue(objIndex,0) + para2(7)*inValue(objIndex,1) + para2(8));;

        return (obj2 - obj1) / (2 * DERIV_STEP);
    }

    //求偏导2
    double PartialDeriv_2(const Eigen::VectorXd& parameter,int paraIndex,const Eigen::MatrixXd &inValue,int objIndex)
    {
        Eigen::VectorXd para1 = parameter;
        Eigen::VectorXd para2 = parameter;
        para1(paraIndex) -= DERIV_STEP;
        para2(paraIndex) += DERIV_STEP;

        //逻辑
        double obj1 = ((para1(3))*inValue(objIndex,0) + para1(4)*inValue(objIndex,1) + para1(5)) / (para1(6)*inValue(objIndex,0) + para1(7)*inValue(objIndex,1) + para1(8));
        double obj2 = ((para2(3))*inValue(objIndex,0) + para2(4)*inValue(objIndex,1) + para2(5)) / (para2(6)*inValue(objIndex,0) + para2(7)*inValue(objIndex,1) + para2(8));;

        return (obj2 - obj1) / (2 * DERIV_STEP);
    }
public:

    Eigen::MatrixXd operator()(const Eigen::VectorXd& parameter,const QList<Eigen::MatrixXd> &otherArgs)
    {
        Eigen::MatrixXd inValue = otherArgs.at(0);
        int rowNum = inValue.rows();

        Eigen::MatrixXd Jac(rowNum*2, parameter.rows());

        for (int i = 0; i < rowNum; i++)
        {
            //            //第一种方法：直接求偏导
            //            double sx = parameter(0)*inValue(i,0) + parameter(1)*inValue(i,1) + parameter(2);
            //            double sy = parameter(3)*inValue(i,0) + parameter(4)*inValue(i,1) + parameter(5);
            //            double w = parameter(6)*inValue(i,0) + parameter(7)*inValue(i,1) + parameter(8);
            //            double w2 = w*w;

            //            Jac(i*2,0) = inValue(i,0)/w;
            //            Jac(i*2,1) = inValue(i,1)/w;
            //            Jac(i*2,2) = 1/w;
            //            Jac(i*2,3) = 0;
            //            Jac(i*2,4) = 0;
            //            Jac(i*2,5) = 0;
            //            Jac(i*2,6) = -sx*inValue(i,0)/w2;
            //            Jac(i*2,7) = -sx*inValue(i,1)/w2;
            //            Jac(i*2,8) = -sx/w2;

            //            Jac(i*2+1,0) = 0;
            //            Jac(i*2+1,1) = 0;
            //            Jac(i*2+1,2) = 0;
            //            Jac(i*2+1,3) = inValue(i,0)/w;
            //            Jac(i*2+1,4) = inValue(i,1)/w;
            //            Jac(i*2+1,5) = 1/w;
            //            Jac(i*2+1,6) = -sy*inValue(i,0)/w2;
            //            Jac(i*2+1,7) = -sy*inValue(i,1)/w2;
            //            Jac(i*2+1,8) = -sy/w2;

            //第二种方法: 计算求偏导

            Jac(i*2,0) = PartialDeriv_1(parameter,0,inValue,i);
            Jac(i*2,1) = PartialDeriv_1(parameter,1,inValue,i);
            Jac(i*2,2) = PartialDeriv_1(parameter,2,inValue,i);
            Jac(i*2,3) = 0;
            Jac(i*2,4) = 0;
            Jac(i*2,5) = 0;
            Jac(i*2,6) = PartialDeriv_1(parameter,6,inValue,i);
            Jac(i*2,7) = PartialDeriv_1(parameter,7,inValue,i);
            Jac(i*2,8) = PartialDeriv_1(parameter,8,inValue,i);

            Jac(i*2+1,0) = 0;
            Jac(i*2+1,1) = 0;
            Jac(i*2+1,2) = 0;
            Jac(i*2+1,3) = PartialDeriv_2(parameter,3,inValue,i);
            Jac(i*2+1,4) = PartialDeriv_2(parameter,4,inValue,i);
            Jac(i*2+1,5) = PartialDeriv_2(parameter,5,inValue,i);
            Jac(i*2+1,6) = PartialDeriv_2(parameter,6,inValue,i);
            Jac(i*2+1,7) = PartialDeriv_2(parameter,7,inValue,i);
            Jac(i*2+1,8) = PartialDeriv_2(parameter,8,inValue,i);

        }
        return Jac;
    }
};
//求单应性矩阵H
Eigen::Matrix3d  CameraCalibration::GetHomography(const Eigen::MatrixXd& src,const Eigen::MatrixXd& dst)
{

    //获取初始单应性矩阵 -- svd
    Eigen::VectorXd H = GetInitialH(src,dst);
    QList<Eigen::MatrixXd> otherValue{src,dst};
    //非线性优化 H 参数 -- LM算法

    H =GlobleAlgorithm::getInstance()->LevenbergMarquardtAlgorithm(H,otherValue,HomographyResidualsVector(),HomographyJacobi());
    H /= H(8);
    // std::cout<<"H:"<<std::endl<<H<<std::endl;

    return  H.reshaped<RowMajor>(3,3);
}

5：求解理想无畸变情况下的摄像机的内参数和外参数

在求取了单应性矩阵后, 还要进一步求出摄像机的内参数。首先令 $h_{i}$
表示 $H$ 的每一列向量, 于是有:

$\left[\begin{array}{lll} h_{1} & h_{2} & h_{3} \end{array}\right]=\lambda K\left[\begin{array}{lll} r_{1} & r_{2} & t \end{array}\right]$

又因为 $r_{1}$ 和 $r_{2}$ 是单位正交向量, 所以有 :

$\begin{aligned} h_{1}^{T} K^{-T} K^{-1} h_{2} & =0 \\ h_{1}^{T} K^{-T} K^{-1} h_{1} & =h_{2}^{T} K^{-T} K^{-1} h_{2} \end{aligned}$
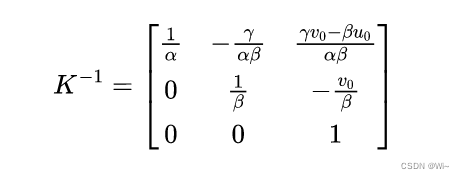
在这里插入图片描述

则：
在这里插入图片描述

这样就为内参数的求解提供了两个约束方程，令：
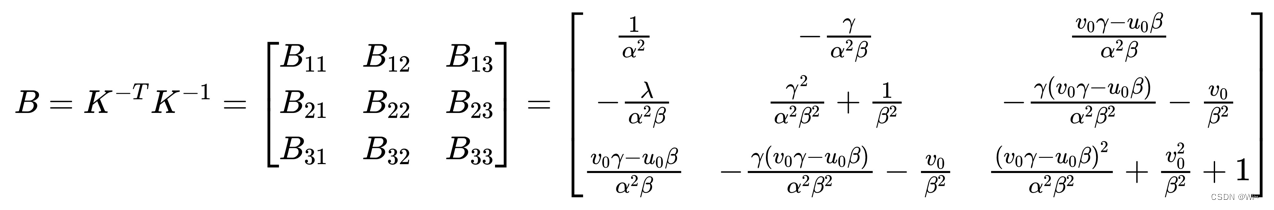在这里插入图片描述由于 $B$ 为对称矩阵, 所以它可以由一个 6 维向量来定义, 即:
$b=\left[\begin{array}{llllll} B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33} \end{array}\right]^{T}$

$h_{i}=\left[\begin{array}{lll}h_{i 1} & h_{i 2} & h_{i 3}\end{array}\right]^{T} , 则:$
$h_{i}^{T} B h_{j}=V_{i j}^{T} b$

其中：
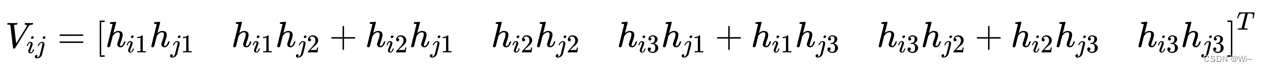
在这里插入图片描述
所以组成一个方程组为：
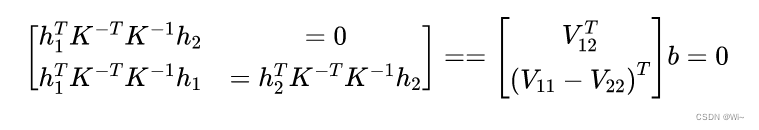$V 为 2 n * 6 矩阵$ 。如果 $n ＞ = 3$ ,则可以列出6个方程，从而解出6个内参数。这6个解出的内部参数不是唯一的，而是通过了一个比例因子缩放。求出内参：

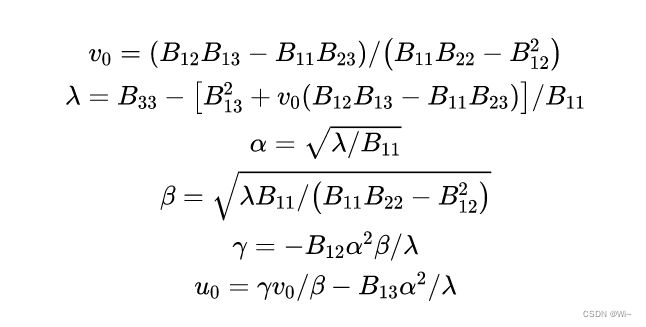
即可求出相机内参矩阵：
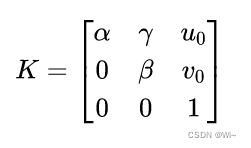
在这里插入图片描述

内参求出后，求外参：
再根据 $\left[\begin{array}{lll} \mathbf{h}_{1} & \mathbf{h}_{2} & \mathbf{h}_{3} \end{array}\right]=\lambda \mathbf{A}\left[\begin{array}{lll} \mathbf{r}_{1} & \mathbf{r}_{2} & \mathbf{t} \end{array}\right]$ 化简可得外部参数，即:

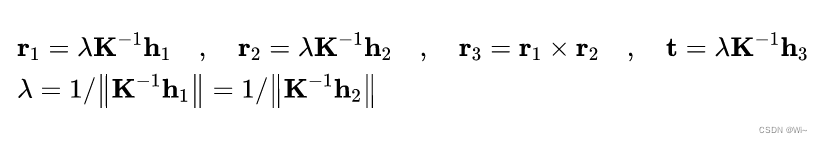
在这里插入图片描述
代码实现：

//根据单应性矩阵H返回pq位置对应的v向量
Eigen::VectorXd CameraCalibration::CreateV(int p, int q,const Eigen::Matrix3d& H)
{
    Eigen::VectorXd v(6,1);

    v << H(0, p) * H(0, q),
            H(0, p) * H(1, q) + H(1, p) * H(0, q),
            H(1, p) * H(1, q),
            H(2, p) * H(0, q) + H(0, p) * H(2, q),
            H(2, p) * H(1, q) + H(1, p) * H(2, q),
            H(2, p) * H(2, q);
    return v;

}
//求相机内参
Eigen::Matrix3d  CameraCalibration::GetIntrinsicParameter(const QList<Eigen::Matrix3d>& HList)
{
    int HCount = HList.count();
    //构建V矩阵
    Eigen::MatrixXd V(HCount*2,6);
    for(int i=0;i<HCount;++i)
    {
        V.row(i*2) = CreateV(0, 1, HList.at(i)).transpose();
        V.row(i*2+1) = (CreateV(0, 0, HList.at(i)) - CreateV(1, 1, HList.at(i))).transpose();
    }

    //Vb = 0
    //svd分解求x
    JacobiSVD<Eigen::MatrixXd> svd(V, Eigen::ComputeFullU | Eigen::ComputeFullV);
    //获取V矩阵最后一列就是b的值
    Eigen::VectorXd b = svd.matrixV().rightCols(1);
    double B11 = b(0);
    double B12 = b(1);
    double B22 = b(2);
    double B13 = b(3);
    double B23 = b(4);
    double B33 = b(5);

    double v0 = (B12*B13 - B11*B23) /  (B11*B22 - B12*B12);
    double lambda = B33 - (B13*B13 + v0*(B12*B13 - B11*B23))/B11;
    //double lambda = 1.0;
    double alpha = qSqrt(lambda / B11);
    double beta = qSqrt(lambda*B11 / (B11*B22 - B12 *B12));
    double gamma = (- B12*alpha*alpha*beta) / lambda;
    double u0 = (gamma*v0 / beta) - (B13 * alpha * alpha / lambda);

    Eigen::Matrix3d K;
    if(m_intrinsicCount == 5)
    {
        K<<alpha,gamma,u0,
                0,beta,v0,
                0,0,1;
    }
    else if(m_intrinsicCount == 4)
    {
        K<<alpha,0,u0,
                0,beta,v0,
                0,0,1;
    }

    return  K;
}


//求相机外参
QList<Eigen::MatrixXd>  CameraCalibration::GetExternalParameter(const QList<Eigen::Matrix3d>& HList,const Eigen::Matrix3d& intrinsicParam)
{
    QList<Eigen::MatrixXd> exterParame;
    //内参逆矩阵
    Eigen::Matrix3d intrinsicParamInv = intrinsicParam.inverse();
    int HCount = HList.count();
    for(int i=0;i<HCount;++i)
    {
        Eigen::Matrix3d H = HList.at(i);
        Eigen::Vector3d h0,h1,h2;
        h0 = H.col(0);
        h1 = H.col(1);
        h2 = H.col(2);

        Eigen::Vector3d  r0,r1,r2,t;
        //比例因子λ
        double scaleFactor = 1 / (intrinsicParamInv * h0).lpNorm<2>();
        r0 = scaleFactor * (intrinsicParamInv * h0);
        r1 = scaleFactor * (intrinsicParamInv * h1);
        r2 = r0.cross(r1);
        t = scaleFactor * (intrinsicParamInv * h2);
        Eigen::MatrixXd Rt(3,4);
        Rt.col(0) = r0;
        Rt.col(1) = r1;
        Rt.col(2) = r2;
        Rt.col(3) = t;
        exterParame.append(Rt);
        // std::cout<<"Rt"<<i<<":"<<std::endl<<Rt<<std::endl;
    }

    return exterParame;
}

//无畸变优化
    Eigen::VectorXd disCoeff1(0);
    //GetDistortionCoeff(srcL,dstL,A,W,disCoeff);
    OptimizeParameter(srcL,dstL,A,disCoeff1,W);

6：应用最小二乘求出实际的畸变系数

相机主要包括径向畸变和切向畸变
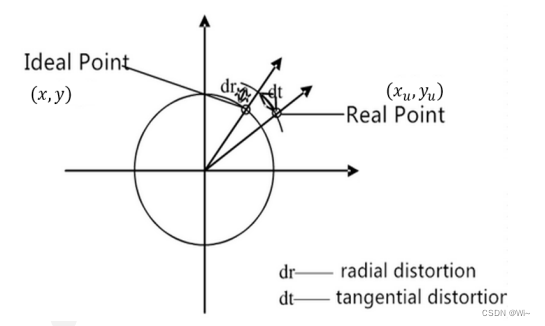
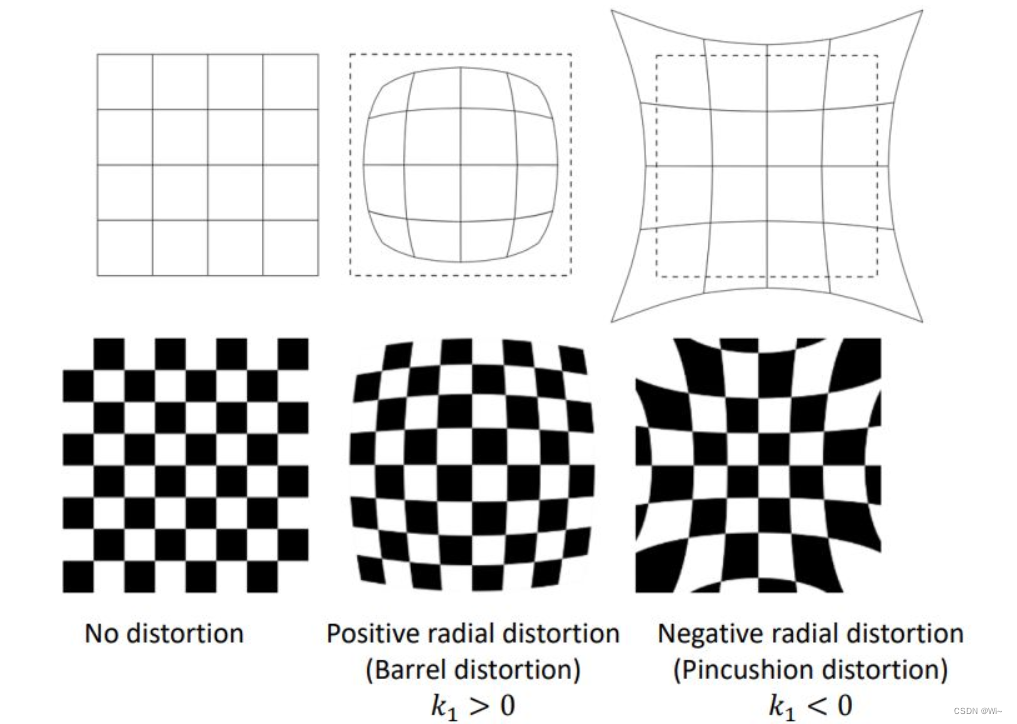
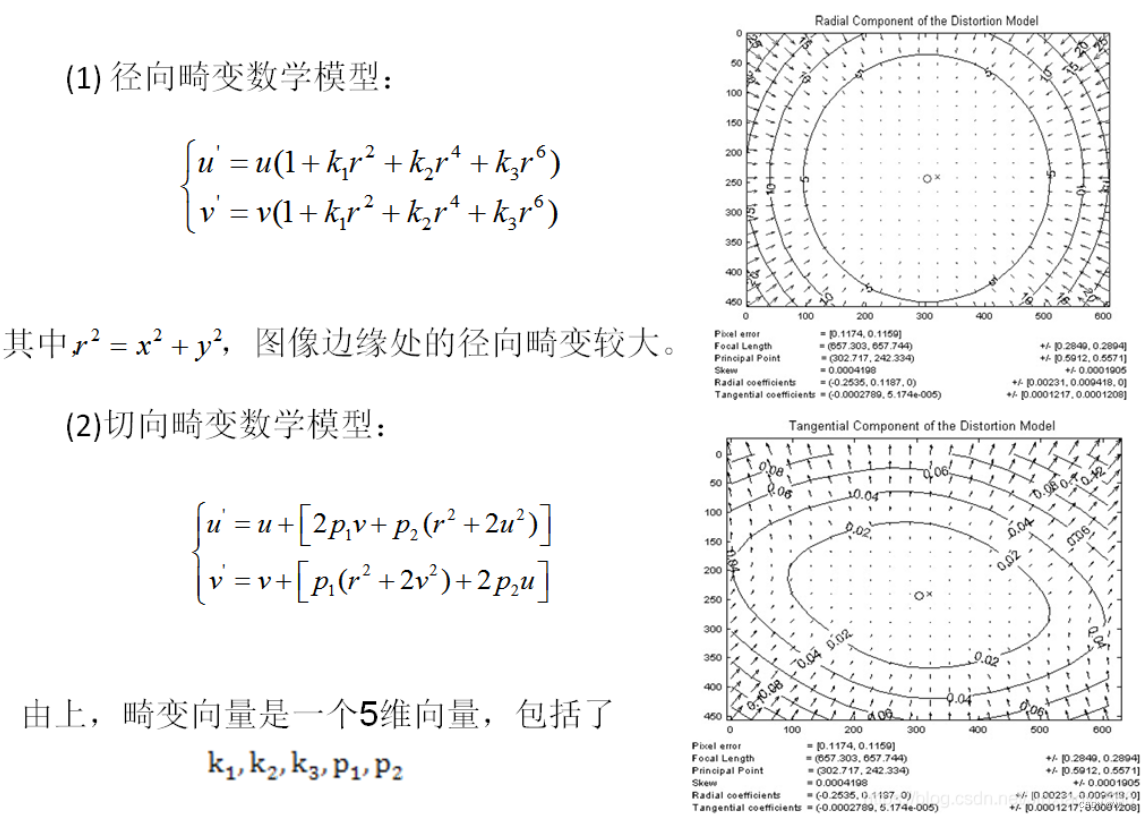
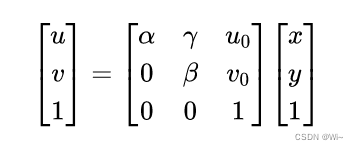在这里插入图片描述

在这里插入图片描述代码实现：

//获取畸变系数 k1,k2,[p1,p2,[k3]]
void CameraCalibration::GetDistortionCoeff(const QList<Eigen::MatrixXd>&  srcL,const  QList<Eigen::MatrixXd>&  dstL,const Eigen::Matrix3d& intrinsicParam ,const QList<Eigen::MatrixXd>& externalParams,Eigen::VectorXd & disCoeff)
{
    //按照畸变个数获取参数
    int disCount = disCoeff.rows();

    if(!(disCount == 2 || disCount == 4 || disCount == 5))
    {
        qDebug()<<QString("畸变参数个数按照数组大小为2或者4或者5,请重新设置数组大小！");
        return;
    }
    int count = srcL.count();
    double u0 = intrinsicParam(0,2);
    double v0 = intrinsicParam(1,2);
    int rowS = 0;
    int k =  0;
    //获取数据个数
    for(int i=0;i<count;++i)
    {
        rowS += srcL.at(i).rows();
    }
    //初始化数据大小
    Eigen::MatrixXd D(rowS*2,disCount),d(rowS*2,1);
    for(int i=0;i<count;++i)
    {
        Eigen::MatrixXd src = srcL.at(i);
        int dataCount = src.rows();
        Eigen::MatrixXd dst = dstL.at(i);
        Eigen::MatrixXd externalParam = externalParams.at(i);

        for(int j=0;j<dataCount;++j)
        {
            //转换齐次坐标
            Eigen::VectorXd singleCoor(4);
            singleCoor(0) = src(j,0);
            singleCoor(1) = src(j,1);
            singleCoor(2) = 0.0;
            singleCoor(3) = 1.0;

            //用现有的内参及外参求估计图像坐标
            Eigen::VectorXd imageCoorEstimate = intrinsicParam * externalParam * singleCoor;
            //归一化图像坐标
            double u_estimate = imageCoorEstimate(0)/imageCoorEstimate(2);
            double v_estimate = imageCoorEstimate(1)/imageCoorEstimate(2);

            //相机坐标系下的坐标
            Eigen::VectorXd normCoor = externalParam * singleCoor;
            //归一化坐标
            normCoor /= normCoor(2);

            double r = std::sqrt(std::pow(normCoor(0),2) + std::pow(normCoor(1),2));

            //k1,k2
            if(disCount >= 2)
            {
                D(k,0) = (u_estimate - u0)*std::pow(r,2);
                D(k,1) = (u_estimate - u0)*std::pow(r,4);

                D(k+1,0) = (v_estimate - v0)*std::pow(r,2);
                D(k+1,1) = (v_estimate - v0)*std::pow(r,4);
            }
            //k1,k2,p1,p2
            if(disCount >= 4)
            {
                D(k,2) = (u_estimate - u0)*(v_estimate - v0)*2;
                D(k,3) = 2 * std::pow((u_estimate - u0),2) + std::pow(r,2);

                D(k+1,2) = 2 * std::pow((v_estimate - v0),2) + std::pow(r,2);
                D(k+1,3) = (u_estimate - u0)*(v_estimate - v0)*2;
            }
            //k1,k2,p1,p2,k3
            if(disCount >= 5)
            {
                D(k,4) = (u_estimate - u0)*std::pow(r,6);

                D(k+1,4) = (v_estimate - v0)*std::pow(r,6);
            }
            d(k,0) = dst(j,0) - u_estimate;
            d(k+1,0) = dst(j,1) - v_estimate;
            k += 2;
        }
    }
    // 最小二乘求解畸变系数
    disCoeff = GlobleAlgorithm::getInstance()->LeastSquares(D,d);

}