基础原理
直方图操作是基于像素统计的基础图像操作,被广泛运用于调整图像的对比度,并由此衍生出很多变种和该经的方式.
图像相直方图
直方图(Histogram),又称质量分布图,是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横坐标表示数据类型,纵轴表示分布情况。
图像直方图,常见的是指根据灰度来绘制灰度的直方图,当然我们也可以绘制RGB直方图,梯度直方图,方向直方图等等,简而言之就是通过直方图的形式来刻画图片的某一属性。
直方图均衡化
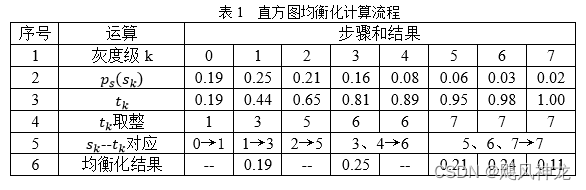
直方图均衡化顾名思义,是将分布不均衡的直方图变为均衡的,如下图所示,将左侧的直方图转换为右侧的直方图整个过程就称作直方图均衡化。
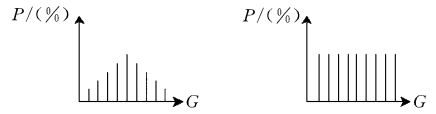
本质上是将分布不均匀的像素强度值,通过单调非线性函数的映射形成均匀的像素强度值分布。
其实现方式具体实现如下:
假设原图像为目标图像为
,那么则有

其具体的计算过程如下:
- 统计图像的直方图信息,并划分到L-1层级上

- 针对每一层级,对统计的像素值进行归一化
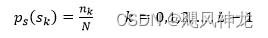
- s的累积分布函数为
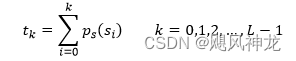
- 对tk取整扩展后
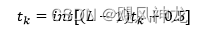
总结整个过程为:
直方图规定化
直方图均衡化能自动增强图像的整体对比度,但是往往结果难以受到控制。实际中常常需要增强某个特定灰度值范围内的对比度或使图像灰度值的分布满足特定需求。这个时候使用直方图规定化会有较好的结果。直方图规定化就是要调整原始图像的直方图去逼近规定的目标直方图。
其具体的计算过程如下:
- 求出原始图像的直方图分布
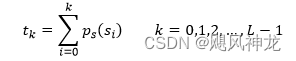
- 求出目标图像的直方图分布
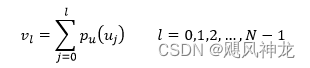
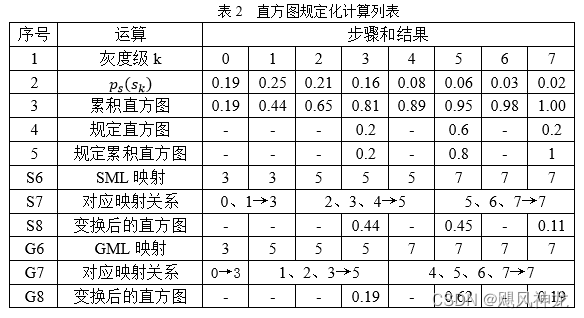
- 接下来就是如何建立原始灰度级数和规定直方图灰度级数的对应映射关系。映射规则一般有两种:单映射规则(SML)和组映射规则(GML)。
单映射规则中,将k从小到大依次找到能使下式有最小值的l的值,这样就可以将原始图像灰度级数k和规定直方图灰度级数l对应映射起来。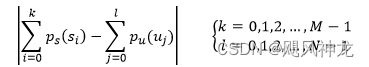
组映射规则中,设I(l)为整数函数,l=1,2,3,…,N-1,满足0≤I(0)≤…≤I(l)≤…≤I(N-1)≤M-1。I(l)为不确定值,因此要确定能使下式达到最小的I(l)*值: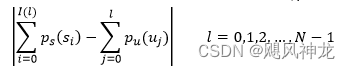
总结整个过程为:
自适应直方图均衡化
实际上“自适应”在这所指的是就是用滑动窗口来对局部的来做直方图均衡化,并且对这个局部区域内的对比度进行限制。
具体计算过程如下:
- 将图信息按窗口大小进行切分
- 在每个窗口内进行直方图均衡化
由于有局部噪声的存在,可能将局部的噪声放大,因此一般在使用自适应直方图均衡化时,常常会对其对比度进行一个限制,防止噪声过度放大,即在映射时添加限制,这种方法也称为对比度受限的自适应直方图均衡化。

API介绍
直方图统计
split(
const Mat &src, //输入图像
Mat* mvbegin //输出的多通道图像数组
)
calcHist(
const Mat* image,//输入图像指针
int images_nums,//输入图像的数目
const int* channels,//输入图像的通道数
InputArray mask, //输入mask,可选,默认不用
OutputArray hist, //输出的直方图数据
int dims, //输出数据的维度
const int* histsize,//直方图的级数(输出多少个条)
const float* ranges,//值域范围(横坐标的范围)
bool uniform, //是否归标准化
bool accumulate //是否累加,如果是多通道的则需要设为true,默认为false
)直方图均衡化
equalizeHist(
InputArray src,//输入图像,必须是8-bit的单通道图像
OutputArray dst//输出结果
)
直方图规定化(直方图匹配)
equalizeHist
(
InputArray src, //原图像
OutputArray dst, //目标图像
Stream &stream = Stream::Null() //异步实时处理的流,通常不用
)自适应直方图均衡化
//创建自适应均衡化器
createCLAHE ( double clipLimit = 40.0, //对比度限制大小
Size tileGridSize = Size(8, 8) //滑窗大小
)
//调用
CLAHE::apply( InputArray src, //原图像
OutputArray dst //目标图像
) 实践一下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 加载图像
image = cv2.imread('lena.png', cv2.IMREAD_GRAYSCALE)
# 直方图均衡化
equalized = cv2.equalizeHist(image)
# 自适应直方图均衡化
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
adaptive_equalized = clahe.apply(image)
# 直方图匹配
def histogram_matching(source, template):
oldshape = source.shape
source = source.ravel()
template = template.ravel()
s_values, bin_idx, s_counts = np.unique(source, return_inverse=True, return_counts=True)
t_values, t_counts = np.unique(template, return_counts=True)
s_quantiles = np.cumsum(s_counts).astype(np.float64)
s_quantiles /= s_quantiles[-1]
t_quantiles = np.cumsum(t_counts).astype(np.float64)
t_quantiles /= t_quantiles[-1]
interp_t_values = np.interp(s_quantiles, t_quantiles, t_values)
return interp_t_values[bin_idx].reshape(oldshape)
template_image = cv2.imread('shan.jpeg', cv2.IMREAD_GRAYSCALE)
matched = histogram_matching(image, template_image)
# 显示结果
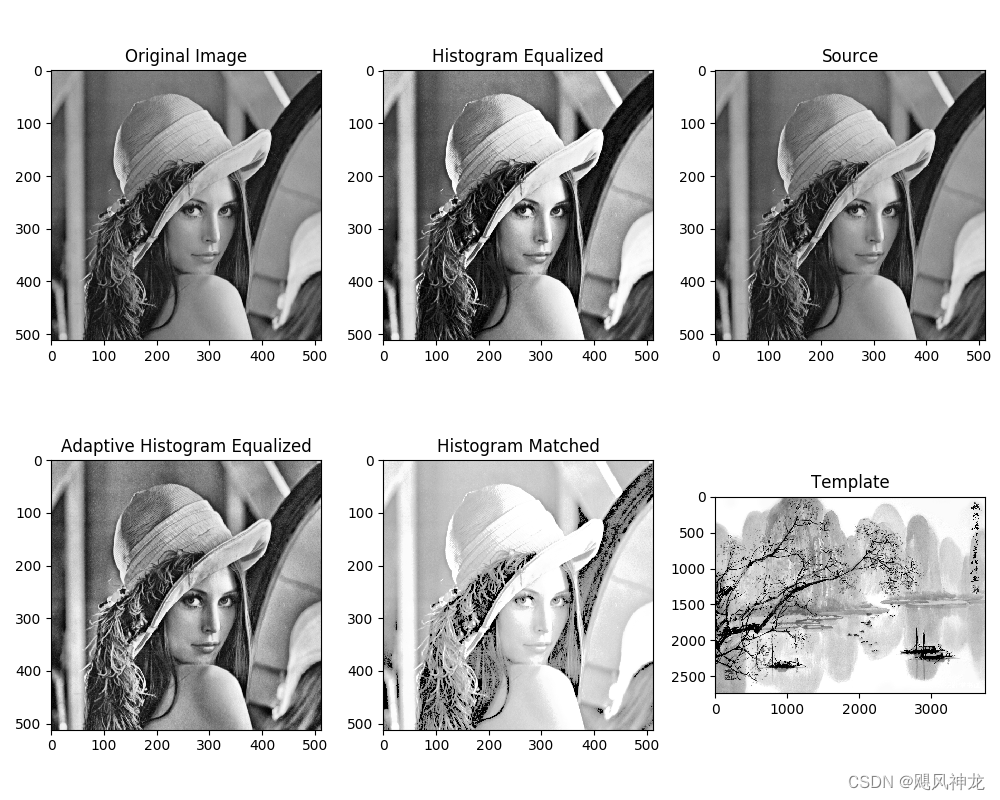
plt.figure(figsize=(10, 8))
plt.subplot(2, 3, 1)
plt.title('Original Image')
plt.imshow(image, cmap='gray')
plt.subplot(2, 3, 2)
plt.title('Histogram Equalized')
plt.imshow(equalized, cmap='gray')
plt.subplot(2, 3, 4)
plt.title('Adaptive Histogram Equalized')
plt.imshow(adaptive_equalized, cmap='gray')
plt.subplot(2, 3, 5)
plt.title('Histogram Matched')
plt.imshow(matched, cmap='gray')
plt.subplot(2, 3, 3)
plt.title('Source')
plt.imshow(image, cmap='gray')
plt.subplot(2, 3, 6)
plt.title('Template')
plt.imshow(template_image, cmap='gray')
plt.tight_layout()
plt.show()
参考链接
直方图均衡化、自适应直方图均衡化_直方图均衡化和自适应均衡化的区别-CSDN博客
限制对比度自适应直方图均衡化算法原理、实现及效果-CSDN博客
直方图均衡化以及直方图匹配_自适应直方图均衡化比直方图均衡化好在哪里-CSDN博客
OpenCV--021:直方图规定化_opencv 直方图规定化-CSDN博客