目录
一.宽度优先搜索(BFS)是什么?
二.图解宽搜(BFS)
三.对比与发现
四。工具——队列
五.模板
六.最后
一.宽度优先搜索(BFS)是什么?
百度百科这样说:
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
过于理论性,不过说出了核心:
它是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
也有人这样说:
就是从根结点位置开始遍历,遍历结束后依次遍历与根节点相邻的点,相邻点遍历结束后继续遍历上轮第一个遍历结点的相邻的未遍历的点,直至所有的点都遍历结束。generalKnowledge/基础算法/广度优先搜索.md · jimmyflower6/中山一中初中部信息竞赛 - Gitee.com
这个说的比较好,但仍然有一点生硬。
简单来说,就是:
宽度优先搜索是一种对图进行搜索的算法。假设我们一开始位于某个顶点(即起点),此 时并不知道图的整体结构,而我们的目的是从起点开始顺着边搜索,直到到达指定顶点(即终 点)。在此过程中每走到一个顶点,就会判断一次它是否为终点。广度优先搜索会优先从离起点 近的顶点开始搜索。
下面,我将用步骤图的方式,向大家介绍这种方法。
二.图解宽搜(BFS)
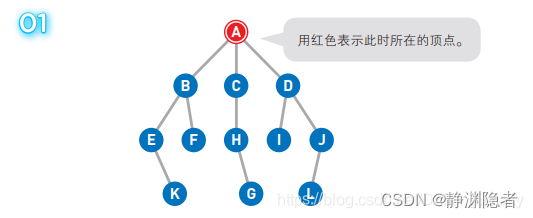
A为起点,G为终点。一开始我们在起点A上,此时并不知道G在哪里。
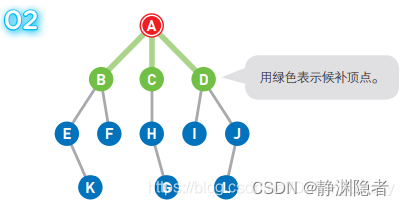
将可以从A直达的三个顶点B、C、D设为下一步的候补顶点。

从候补顶点中选出一个顶点。优先选择最早成为候补的那个顶点,如果多个顶点同时成为候补,那么可以随意选择其中一个。 (优先选择最早成为候补的那个顶点,这是一种“先进先出”的方式,后面会讲到)

此处 B、C、D 同时成为候补,所以我们随机选择了最左边的顶点B。

移动到选中的顶点B上。此时我们在B上, 所以B变为红色,同时将已经搜索过的顶点变为橙色。
此处,候补顶点是用“先入先出”(FIFO)的方式来管理的,因此可以使用“队列”这个数据结构。(这个结构将会在后面讲解,请往下翻)
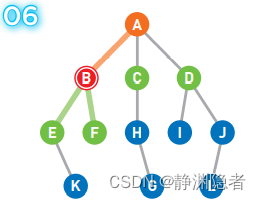
将可以从B直达的两个顶点E和F设为候补 顶点。
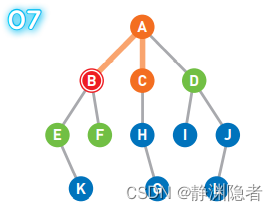
此时,最早成为候补顶点的是C和D,我们选择了左边的顶点C。

移动到选中的顶点C上。
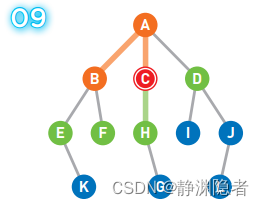
将可以从C直达的顶点H设为候补顶点。
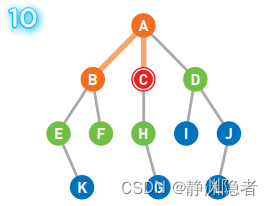
重复上述操作直到到达终点,或者所有的顶点都被遍历为止。

这个示例中的搜索顺序为 A、B、C、D、E、F、 H、I、J、K。
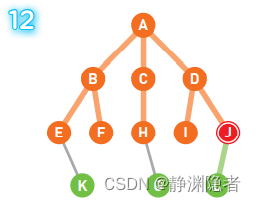
完成了从A到I的搜索,现在在顶点J处。
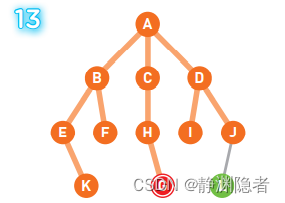
到达终点G,搜索结束。
补充说明:由上可以知道,广度优先搜索的特征为从起点开始,由近及远进行广泛的搜索。因此,目标顶点离起点越近,搜索结束得就越快。
三.对比与发现
DFS和BFS的区别
bfs 遍历节点是先进先出,dfs遍历节点是先进后出;
bfs是按层次访问的,dfs 是按照一个路径一直访问到底,当前节点没有未访问的邻居节点时,然后回溯到上一个节点,不断的尝试,直到访问到目标节点或所有节点都已访问。
bfs 适用于求源点与目标节点距离最近的情况,例如:求最短路径。dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况,例如:全排列、拓扑排序、求到达某一点的任意一条路径。
不过,宽度优先搜索(BFS)的先进先出如何实现呢?这里,我们运用了一个数据结构——队列。
四。工具——队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
我们可以用双指针标记一下,通过front指针与rear指针,对队头和队尾进行标记,然后只允许在front、rear指针的位置进行增删改查,那么这样便实现了对数组的受限。这是一种运用数组的数据结构对队列的模拟。初学者建议先用这种方式熟悉队列。
具体操作:
/*
通常将front赋值为0,rear赋值为-1
方便后续进队、出队以及取队首元素
*/
int a[100], front=0, rear=-1;
// 进队
a[++rear] = 10;
// 出队
front++
// 取队首元素
a[front]
// 取队尾元素
a[rear]
// 判断是否为空队
if(front > rear)
cout << "该队列为空队";
不过,到了后期,为了节省时间,我们可以直接用c++自带的STL容器来完成操作。
具体操作如下:
// 导入queue包
#include<queue>
// 申明一个queue对象
// 填入你想装填的数据类型
queue<int> qu;
// 进队
int a = 10;
qu.push(a);
// 出队,无返回值
qu.pop();
// 取队首元素
int front = qu.front();
// 取队尾元素
int rear = qu.back();
// 队是否为空
if(qu.empty()) {
cout << "该队列为空队";
}
// 队大小,返回int
qu.size();
五.模板
BFS的题目是有一套明显模板的,不信,我们来看看。(将展示核心代码)
八数码问题:
while(!q.empty())//q非空,可以走
{
for(int i=0;i<4;i++)//四个方向
{
ma ac=q.front();
int nx = ac.x0 + dx[i];
int ny = ac.y0+ dy[i];
if(nx>=1&&ny>=1&&nx<=3&&ny<=3)
{
swap(ac.a[ac.x0][ac.y0],ac.a[nx][ny]);
ac.x0=nx;
ac.y0=ny;
//将0与目标数交换
ac.ans++;//步数加1
ac.kt=kt(ac);
//康托判重
if (!flag[ac.kt])
{
flag[ac.kt] = 1;
q.push(ac);
//加入队列
if(ac.kt==mo.kt)
{
printf("%d",q.back().ans);
exit(0);
}
}
}
}
q.pop();
//弹出已遍历完所有情况的矩阵
}海上救援任务:
while(!q.empty())
{
for(int i=0;i<4;i++)
{
node ne;
ne.x=q.front().x+dx[i],ne.y=q.front().y+dy[i];
if(bo[ne.x][ne.y]==0&&ne.x>=0&&ne.y>=0&&ne.x<=n&&ne.y<=m&&a[ne.x][ne.y]==1)
{
ne.ans=q.front().ans+1;
bo[ne.x][ne.y]=1;
q.push(ne);
if(ne.x==xe.x&&ne.y==xe.y)
{
flag=true;
printf("%d\n",q.back().ans);
break;
}
}
}
if(flag) break;
q.pop();
}巧妙取量:
while(scanf("%d%d%d%d",&t.a[1],&t.a[2],&t.a[3],&k)!=EOF)//多组数据
{
flag=false;
memset(bo,0,sizeof(bo));
bo[t.a[1]][t.a[2]][t.a[3]]=1;
p.ans=0;
p.a[1]=t.a[1];
p.a[2]=p.a[3]=0;
q.push(p);
if(q.front().a[1]==k||q.front().a[2]==k||q.front().a[3]==k)
{
printf("yes\n%d\n",0);
continue;
}//特判
while(!q.empty())
{
for(int i=1;i<=3;i++)
{
if(q.front().a[i]>0)
{
for(int j=1;j<=3;j++)
{
node sy;
sy=q.front();
sy.ans ++;
if(i!=j)
{
int T=t.a[j]-sy.a[j];
if(sy.a[i]>T)
{
sy.a[j]=t.a[j];
sy.a[i]=sy.a[i]-T;
}
else
{
sy.a[j]+=sy.a[i];
sy.a[i]=0;
}
if(!bo[sy.a[1]][sy.a[2]][sy.a[3]])
{
bo[sy.a[1]][sy.a[2]][sy.a[3]]=1;
if(sy.a[1]==k||sy.a[2]==k||sy.a[3]==k)
{
flag=true;
}
q.push(sy);
}
}
}
}
}//遍历每一种倒法
if(flag) break;
q.pop();
}
if(flag)
{
printf("yes\n%d\n",q.back().ans);
}
else
{
printf("no\n");
}
while(!q.empty())
{
q.pop();
}
}我选了几道没那么相似的题目,但仔细一看,架构都是一样的。
用步骤图可表示为:
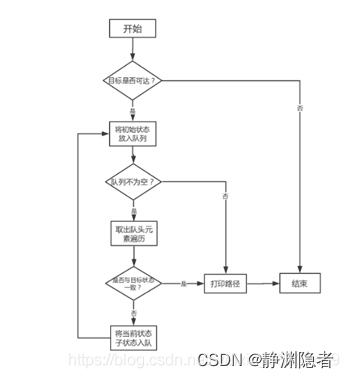
而用伪代码,则是这样表示:
int BFS(Node start, Node target) {
入队(初始状态);
visited[初始状态] = true;
while(!空队) {
for() { // 状态转换
Node node = 队首元素;
对node的处理,生成新node状态;
if (visited[node] == true)
continue;
if (node == target) {
输出答案;
return 0;
}
v[node] = true;
入队(node);
}
}
出队();
}这,就是BFS问题的模板!!!
六.最后
没什么,如果喜欢的话,给个三连吧!您的支持是我最大的动力!