一、思路转变

A为对称正定矩阵，$$Ax=b$$

求解向量$x$这个问题可以转化为一个求$f(x)$极小值点的问题，为什么可以这样：

$$f(x)=\frac{1}{2}{x}^{T}Ax-x^{T}b+c$$

可以发现：

$$\nabla f=\mathrm{grad}f=Ax-b$$

由$A$的正定性可以保证$f(x)$的驻点一定是极小值点。而$Ax-b=0$得到的就是$f(x)$的驻点，即：

$$f(x^{\ast })=\min f(x)\iff \nabla f(x^{\ast })=A{x}^{\ast }-b=0$$

把解线性方程组的问题，转化为求函数$f(x)$的极小值点。

二、最速下降法

怎么找到这个极小值点?

已知一个多元函数沿其负梯度方向函数值下降得最快。

一种较为形象的解释：

想象自己在半山腰上，要到山脚处：

• 首先要找好下降方向：负梯度方向
• 之后沿着选定方向直走
• 走到不能再下降为止（也就是选定方向的最低点），停下来，再找新的下降方向
• 重复上面的过程，便能到达山脚

翻译成数学语言

• 给定任意初值$x_0$，计算残量$r_0=b-A{x}_0$。

• 选择$P=r_0$为前进方向，计算：

  $$\alpha =\frac{\left(r_0,r_0\right)}{\left(A{r}_0,r_0\right)},x_1=x_0+\alpha r_0$$

• 重复上面的过程。

算法如下：

三、北太天元 or matlab实现

最速下降法解线性方程组

function [x,k,r] = Gradient_Descent(A,b,x0,e_tol,N)
    % 最速下降法 解线性方程组
    % Input: A, b(列向量), x0(初始值),e_tol: error tolerant, N: 限制迭代次数小于 N 次             
    % Output: x , k(迭代次数), r
    %   Version:            1.0
    %   last modified:      2024/05/19
    n = length(b); k = 0; 
    R = zeros(1,N); % 记录残差
    r = b - A*x0;
    x = zeros(n,N); % 记录每次迭代结果
    x(:,1) = x0;
    norm_r = norm(r,2); R(1) = norm_r;
    while norm_r > e_tol && k < N
        alpha = r'*r/(r'*A*r);  % 计算步长
        x(:,k+2) = x(:,k+1) + alpha * r;
        r = b - A * x(:,k+2); % 残量
        norm_r = norm(r,2);
        R(k+2)=norm_r;
        k = k+1;
    end
    x = x(:,1:k+1); % 返回每次的迭代结果
    r = R(1:k+1);   % 返回每次的残差
    if k>N
        fprintf('迭代超出最大迭代次数');
    else
        fprintf('迭代次数=%i\n',k);
    end
end

四、数值算例

下面例子中统一 $ N=100,e_tol=10^{-8},x_0 = 0 $

例1

$$Ax=b$$
$$A=\left[\begin{array}{cccc}4& 1& 0& 0\\ 1& 4& 1& 0\\ 0& 1& 4& 1\\ 0& 0& 1& 4\end{array}\right]b=\left[\begin{array}{c}6\\ 25\\ -11\\ 15\end{array}\right]$$

用最速下降法求$x$ ;

实现

clc;clear all,format long;
N = 100; e_tol = 1e-8;
A = [4, 1, 0, 0; 
     1, 4, 1, 0;  
     0, 1, 4, 1; 
     0, 0, 1, 4];
b = [6; 25; -11; 15];
x0 = [0; 0; 0; 0];
[x11, k1, r11] = Gradient_Descent(A, b, x0, e_tol, N);
x_exact = gsem_column(A, b);

% 作图查看误差变化
n = length(b);
k1 = k1 + 1;

% 数值解
figure(1);
plot(1:k1, x11(1,:), '-*r', 1:k1, x11(2,:), '-og', 1:k1, x11(3,:), '-+b', 1:k1, x11(4,:), '-dk');
legend('x_1', 'x_2', 'x_3', 'x_4');
title('每个数值解的变化');

% 残差变化
figure(2);
plot(1:k1, r11, '-*r');
legend('残差');
title('残差变化');

运行后得到

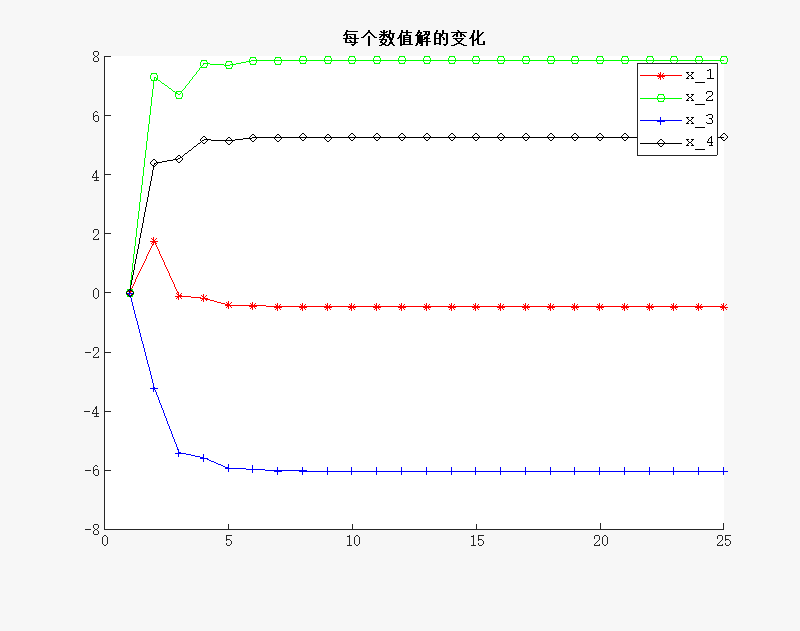
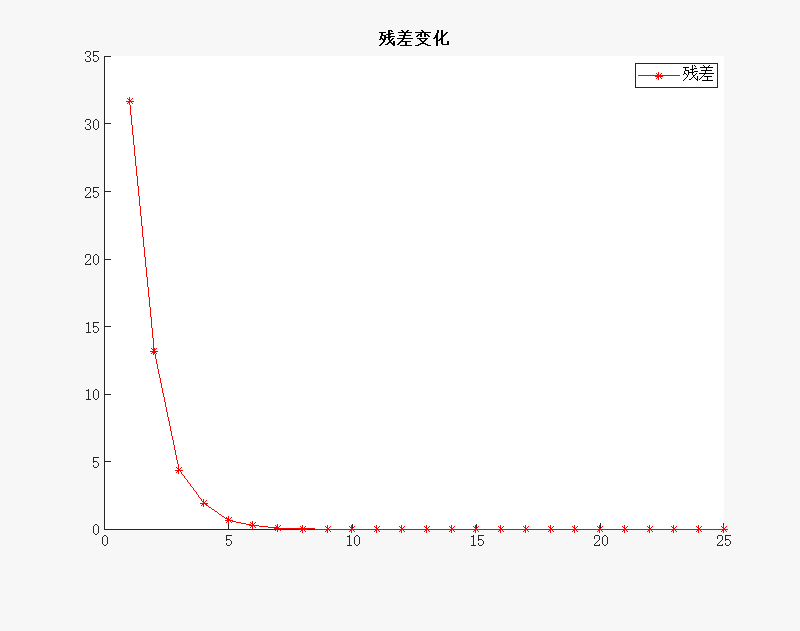
通过这个例子可以初步看到方法是可行的.

例2

下面这个例子我将形象展示最速下降法的实现特点

A = [3 1; 1 5];
b = [-1;1];
c = 0;

对应函数：$$f(x,y)=\frac{1}{2}\left(3x^2+2\cdot 1\cdot xy+5y^2\right)-(-x+y)+0$$

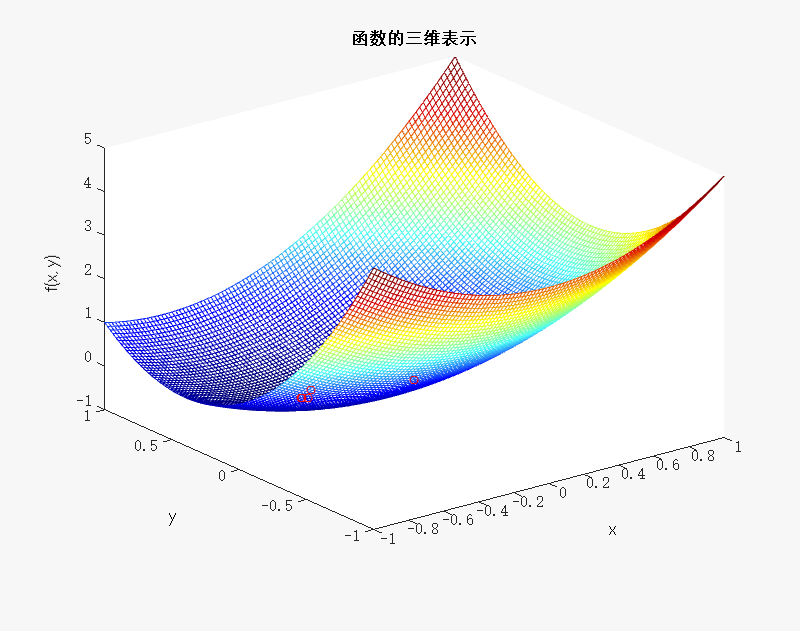
三维表示一下

clc;clear all;format long;
A = [3  1; 1 5]; 
b = [-1;1];
c = 0; 
N = 100; e_tol = 1e-8; x0 =zeros(length(b),1);

%x0 =[-0.1;-0.1]

x = linspace(-1,1,100); 
y = linspace(-1,1,100);
% 网格化、方便作图
[x, y] = meshgrid(x,y);
% 定义函数 f(x) = 0.5 * x' * A * x - x'*b + c
% 为了作图方便,如下定义
f=@(x,y) 0.5 * (A(1,1) * x.^2 + 2 * A(1,2) * x .* y + A(2,2) * y.^2) - (b(1) * x + b(2) * y) + c;
z = f(x,y);

mesh(x,y,z)
[x11,k1,r11] = Gradient_Descent(A,b,x0,e_tol,N);

figure(1)
mesh(x,y,z)
hold on
% 绘制最速下降法的每次迭代点
%scatter3(x11(1, :), x11(2, :), f(x11(1,:),x11(2,:)),'r','filled');
plot3(x11(1, :), x11(2, :), f(x11(1,:),x11(2,:)),'r-o');

xlabel('x');
ylabel('y');
zlabel('f(x, y)');
title('函数的三维表示');
hold off;

运行后得到

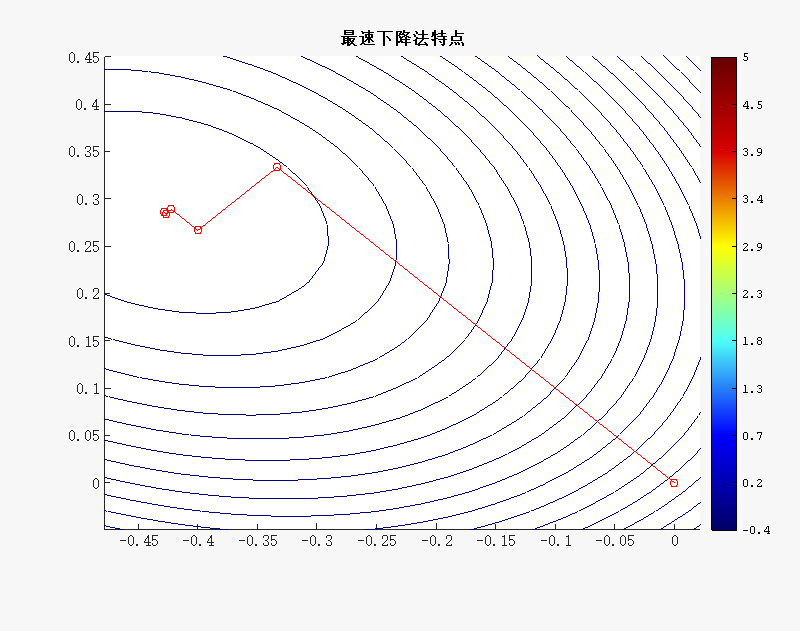
绘制等高线图

figure(2)
hold on 
contour(x,y,z,200)
plot(x11(1, :), x11(2, :), 'r-o');
title('最速下降法特点');
colorbar;

运行后得到

为了展示更清晰,将 $ x_0 $设为 [-0.2;0] ,可以得到这样的图像

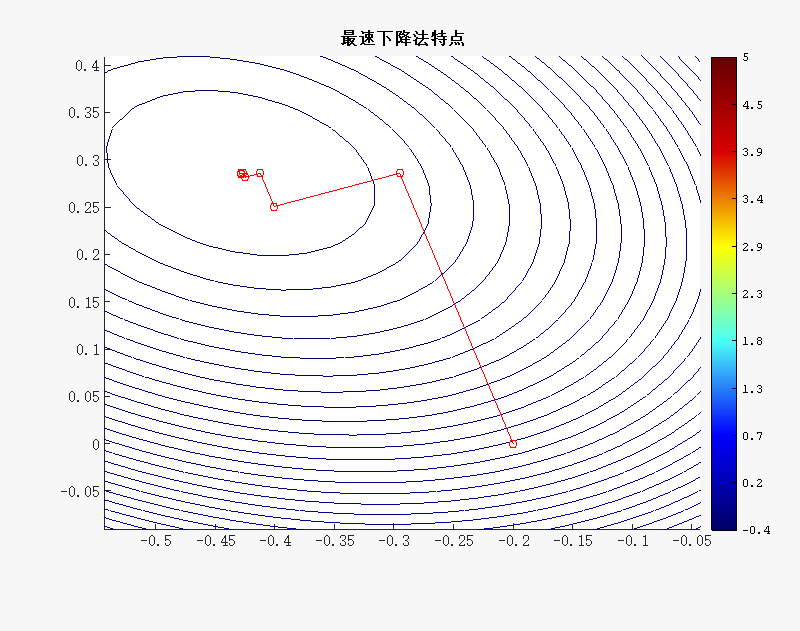
由图形可以看出,最速下降法是如何下降的.

从某一点,选定最快的下降方向,下降到不能再下降为止,再重新找新的最快的下降方向.就这样依次进行下去.

由此可以看出最速下降法的优点是容易理解和实现较为简单.

当然也可以看出它还存在很大的改进空间,在每一次选方向时,明明有着更快更好的方向(三角形任意的第三边都更快).

---

以上图形均在北太天元软件中绘制，matlab同样可以正常运行。