常见的损失函数

损失函数：衡量模型参数的质量的函数，衡量方式是比较网络输出和真实输出的差异。ybar与y 之间的差异
损失函数、代价函数、目标函数、误差函数 虽然叫法不同，但都是一样的。

1、分类任务

在分类任务中最多使用的是交叉熵损失函数，下面分多分类和二分类来讨论交叉熵

1.1 多分类任务

在多分类任务中，使用softmax将logits转换为概率的形式，所以多分类的交叉熵损失也叫做softmax损失

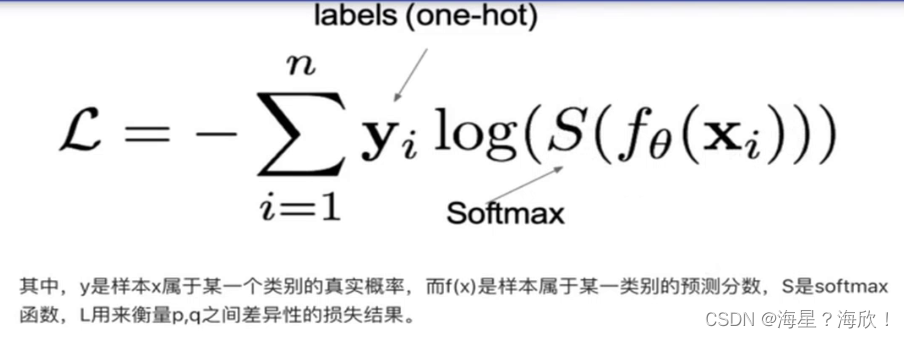
交叉熵损失：最小化正确类别所对应的预测概率的对数的负值

在tf.keras 中使用CategoricalCrossentropy
代码实现：

#交叉熵损失
import tensorflow as tf
#设置真实值和预测值
y_true = [[0,1,0],[0,0,1]]
y_pre1 = [[0.05,0.9,0.05],[0.3,0.2,0.5]]
y_pre2 = [[0.05,0.9,0.05],[0.05,0.05,0.9]]
#实例化交叉熵损失
cce = tf.keras.losses.CategoricalCrossentropy()
#计算损失结果
cce(y_true,y_pre1)  #输出结果为0.39925
cce(y_true,y_pre2)  #输出结果为0.10536

越接近真实值，交叉熵损失值越小

1.2 二分类任务

二分类任务中，不再使用softmax激活函数，而是使用sigmoid激活函数，所以损失函数也相应调整

在tf.keras 中使用BinaryCrossentropy()

import tensorflow as tf
#设置真实值和预测值
y_true = [[0],[1]]
y_pre1 = [[0.4],[0.6]]
y_pre2 = [[0.1],[0.9]]
#实例化交叉熵损失
bce = tf.keras.losses.BinaryCrossentropy()
#计算损失结果
bce(y_true,y_pre1)  #输出结果为0.5108254
bce(y_true,y_pre2)  #输出结果为0.10536041

同样地，越接近真实值，交叉熵损失值越小

2、 回归任务

2.1 MAE损失

MAE损失也称为L1 Loss ，是以绝对误差作为距离
特点：L1 Loss 具有稀疏性，为了惩罚较大的值，常常将其作为正则项添加到其他loss中作为约束，最大问题是梯度在零点不平滑，导致会跳过极小值

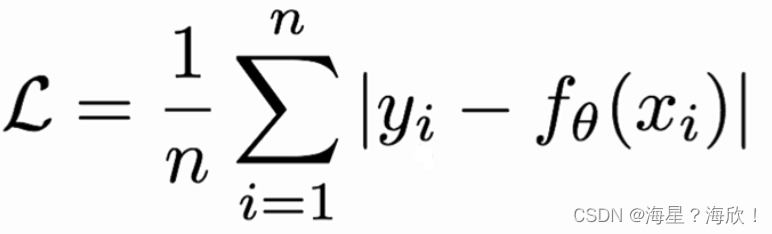
在tf.keras 中使用MeanAbsoluteError()

import tensorflow as tf
#设置真实值和预测值
y_true = [[0.],[1.]]
y_pre1 = [[1.],[0.]]
y_pre2 =  [[0.],[1.]]
#实例化MAE损失
mae = tf.keras.losses.MeanAbsoluteError()
#计算损失结果
mae(y_true,y_pre1)  #输出结果为1.0
mae(y_true,y_pre2)  #输出结果为0

2.2 MSE损失

MSE损失又称为L2 loss ，欧式距离，以误差的平方和作为距离
L2 loss 也称为正则项，当预测值和目标值相差很大时，梯度容易爆炸

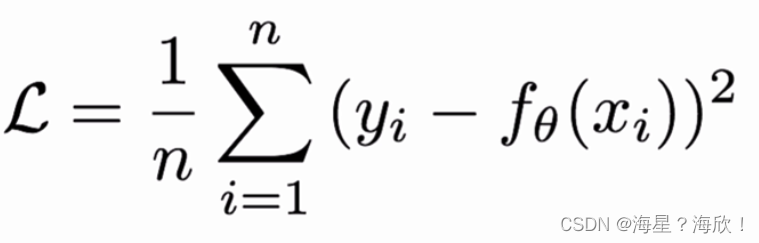
在tf.keras 中使用MeanSquaredError()

import tensorflow as tf
#设置真实值和预测值
y_true = [[0.],[1.]]
y_pre1 = [[1.],[0.]]
y_pre2 =  [[0.],[1.]]
#实例化MAE损失
mae = tf.keras.losses.MeanSquaredError()
#计算损失结果
mae(y_true,y_pre1)  #输出结果为1.0
mae(y_true,y_pre2)  #输出结果为0

越接近真实值，损失函数越小

L2损失用在正则化

2.3 smooth L1损失

将L!和L2损失结合起来，smooth L1损失是最常用的损失函数
下面公式中，x指真实值与预测值之间的差值

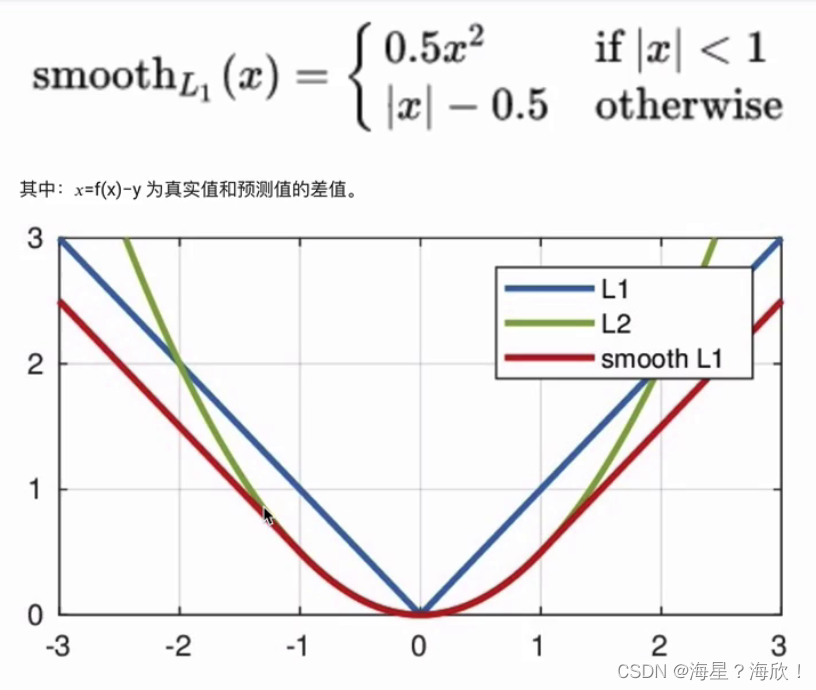
实际上是一个分段函数，[-1,1]区间之间是L2损失，解决了L1的不光滑问题，在[-1,1]区间之外是L1损失，解决了离群点梯度爆炸的问题

在tf.keras 中使用Huber()

import tensorflow as tf
#设置真实值和预测值
y_true = [[0.],[1.]]
y_pre = [[0.2],[0.6]]
#实例化MAE损失
mae = tf.keras.losses.Huber()
#计算损失结果
mae(y_true,y_pre)  #输出结果为0.0499

深度学习一般用于分类任务

总结

多分类问题用多分类的交叉熵函数
二分类问题用二分类的交叉熵函数
回归问题用smooth L1损失