大数据很重要，但是存在体量大、价值密度低的问题，我们该怎么解决

1、 数据价值密度低的解决方案

​ 在所有这些场景中，我们需要将信息缩减到可管理的大小。特征选择是一个过程，可用于选择一组精简的特征，这些特征仍能提供足够的有用信息。这个过程通常是通过删除冗余和不必要的功能来完成的。如果一个特征提供的信息与同一数据集中另一个特征提供的信息相同，则该特征将是冗余的。如果一个特性不能给所需的信息增加任何价值，那么它就是不必要的。

​ 然后，所选择的特征集可以用于进一步的处理，例如，聚类、分类、规则提取，特征的减少可以显著提高这些处理系统的整体性能，例如，考虑具有一千个特征的分类场景，并将其与只有一百个特征的情况进行比较。显然，在考虑所有其他条件相同的情况下，后一种情况花费的时间要少得多。

1.1 粗糙集中对应的概念：属性约简

​ 由于粗糙集概念有些抽象，我们先来看下粗糙集能够达成什么样的效果，让大家能够直观感受粗糙集。

​ 属性约减又叫降维，指在保留知识分类或决策效果几乎不发生变化的前提下，从中删掉冗余信息，它可以有效删除不必要属性，提高决策效率。

1、线性降维方法：主成分分析（PCA）、独立成分分析（ICA）

​ 和线性判别分析（LDA）

2、非线性降维方法：

​ （1）基于核函数的非线性降维方法：KPCA 、KICA

​ （2）基于特征值的非线性降维方法

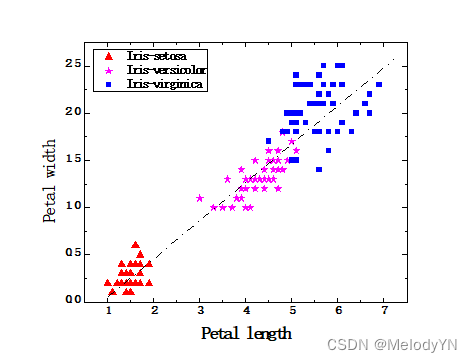
约简前聚类效果和约简后的聚类效果对比，可以检验约简的效果如何。假如约简前是上图，约简后三种形状和颜色的点混合在一起，则说明约简效果很差。

1.2 属性约简的好处

• 去除冗余特征，减少所需的存储空间
• 加快计算速度，更少的维数意味着更少的计算，更少的维数可以允许使用不适合大量维数的算法
• 太多的特征或太复杂的模型可能导致过拟合

1.3 粗糙集的应用

数据预处理阶段：保证后续效率。神经网络训练模型是一个迭代过程，期间会消耗大量的时间。因此，在进入网络前对数据进行约简是非常有意义的，可以大大提升其效率，训练出的模型也会更好。

以阿尔法狗围棋为例对过拟合的再解释：假设AlphaGo和10位选手的10000场下棋结果进行训练，最后得到一个模型。AlphaGo和这10位围棋大师下棋，总能胜利。但是，此时有一位新的围棋高手，AlphaGo没有与之交过手，然后输了。这种情况不是偶然，经常出现，则说明模型过拟合了。真正拟合的模型对新到达的数据依然能够给出正确的决策。

2、粗糙集的简介—>原理

2.1 粗糙集的概念

1982年，波兰数学家Z.Pawlak发表了经典论文Rough Sets， 它是一种刻画不完整性和不确定性的数学工具，能有效地分析不精确，不一致（inconsistent)、不完整（incomplete) 等各种不完备的信息，还可以对数据进行分析和推理，从中发现隐含的知识，揭示潜在的规律。

已被广泛应用于知识发现、机器学习、决策支持、工业控制故障检测、专家系统、推荐系统、图像处理及归纳推理等领域。

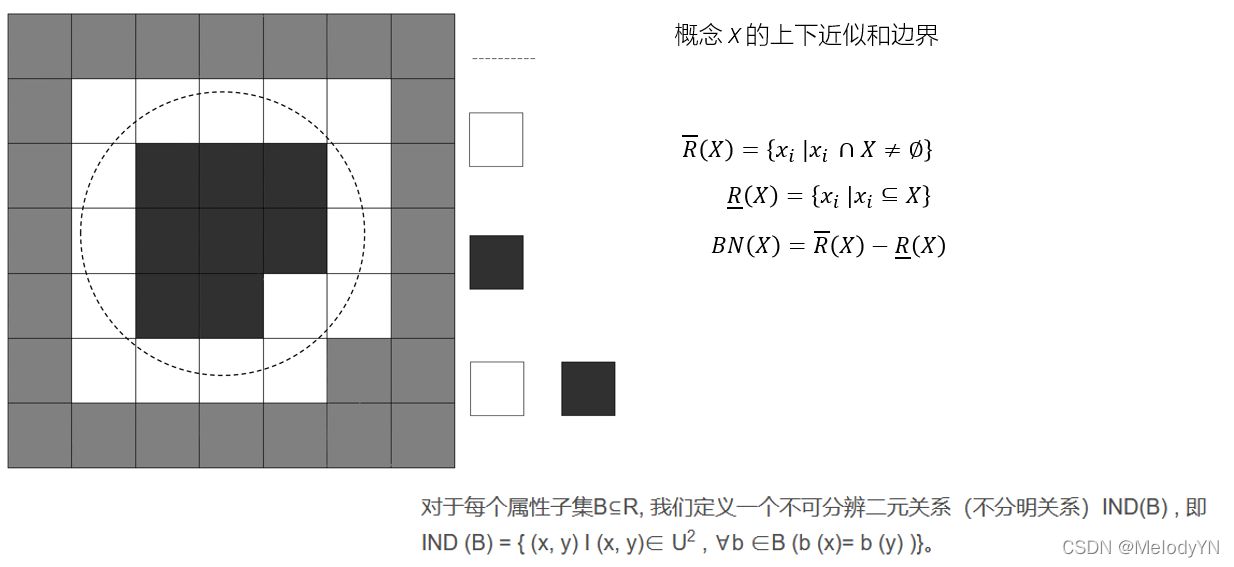
2.2 从例子看粗糙集

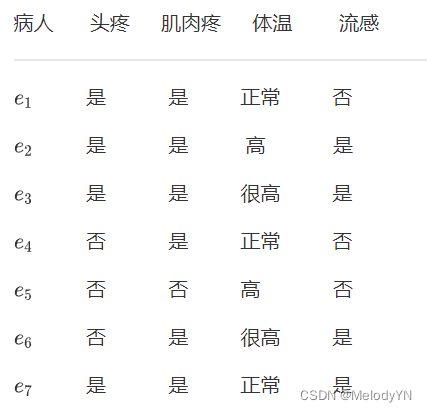
U = { e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 } U=\{e_1,e_2,e_3,e_4,e_5,e_6,e_7\} U={e1​,e2​,e3​,e4​,e5​,e6​,e7​}

令P={“肌肉疼”，“体温”}

等价类：

$U/P$={$e_1$,$e_4$,$e_7$}{$e_2$},{$e_3$,$e_6$},{$e_5$}

是，正常： $X_1$={$e_1$,$e_4$,$e_7$}

是，高： $X_2$={$e_2$}

是，很高： $X_3$={$e_3$,$e_6$}

否，高： $X_4$={$e_5$}

决策

D 1 = { e 1 , e 4 , e 5 } D_1=\{e_1,e_4,e_5\} D1​={e1​,e4​,e5​}

D 2 = { e 2 , e 3 , e 6 , e 7 } D_2=\{e_2,e_3,e_6,e_7\} D2​={e2​,e3​,e6​,e7​}

求各个集合分别与各个决策集合的关系。

$X_1\cap D_1\ne \varnothing$

$X_4\subseteq D_1$

$X_1\cap D_2\ne \varnothing$

$X_2\subseteq D_2$

$X_3\subseteq D_2$

等价类包含于某个决策类-------------->意味着等价类肯定能推出指定决策（确定）。

等价类相交于某几个决策类----------->意味着等价类可能推出指定某几个决策（不确定）。

循环每一种属性组成的可能性，找出最优的属性子集即为属性约简。

最优属性子集：正域尽可能大，属性尽可能少。

2.3 粗糙集模型的分类及其评估标准

依赖度(近似质量)是衡量一个模型优劣的指标。

​ 在保证近似质量的前提下去缩短时间才是有意义的。

3、粗糙集的主要研究方向

3.1 模型创新

3.2 属性约简

遗传算法、优化算法、并行计算

3.3 提高计算效率

• 并行计算
• 增量学习(流计算)
• GPU加速