[Algorithm][动态规划][简单多状态DP问题][买卖股票的最佳时机 III][买卖股票的最佳时机 Ⅳ]详细讲解

news2024/11/17 5:47:46

1.买卖股票的最佳时机 III

1.题目链接

买卖股票的最佳时机 III

2.算法原理详解

注意：本题为了便于初始化，有较多细节服务于它
思路：
- 确定状态表示 -> dp[i]的含义
  - 第i天结束之后，所能获得的最大利润
  - 本题，状态表示还可以继续细分：
    - f[i][j]：第i天结束之后，完成了j次交易，处于“买入”状态，此时的最大利润
    - g[i][j]：第i天结束之后，完成了j次交易，处于“卖出”状态，此时的最大利润
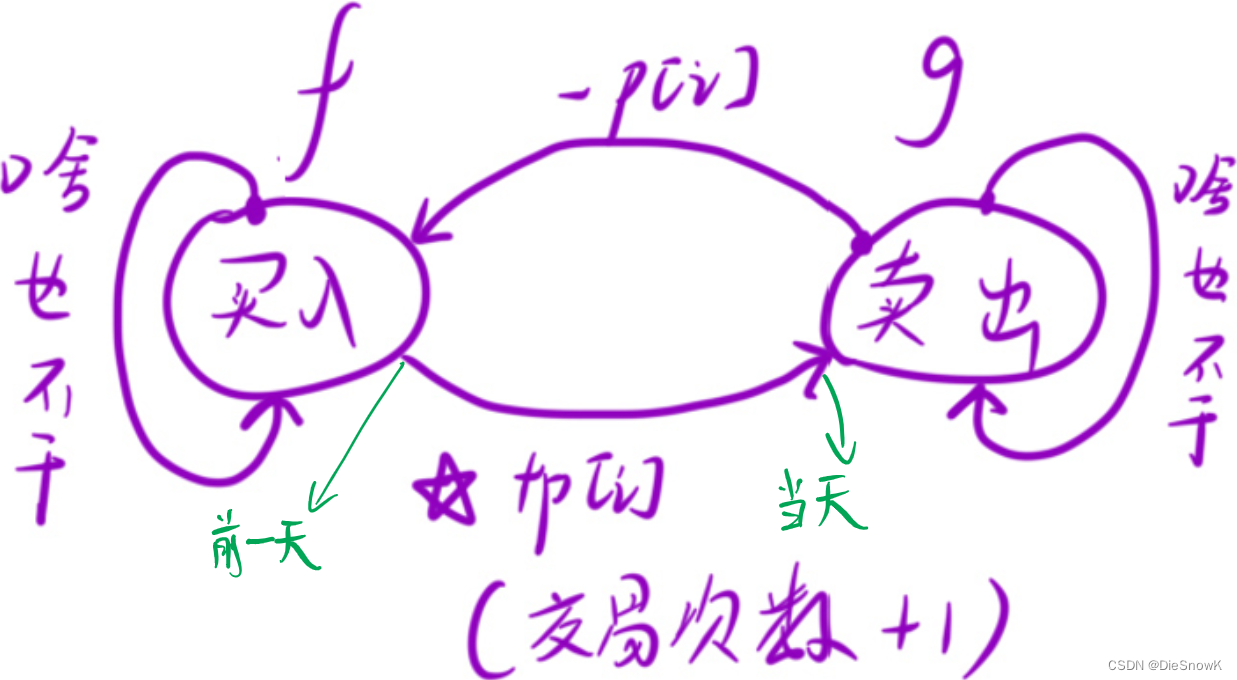
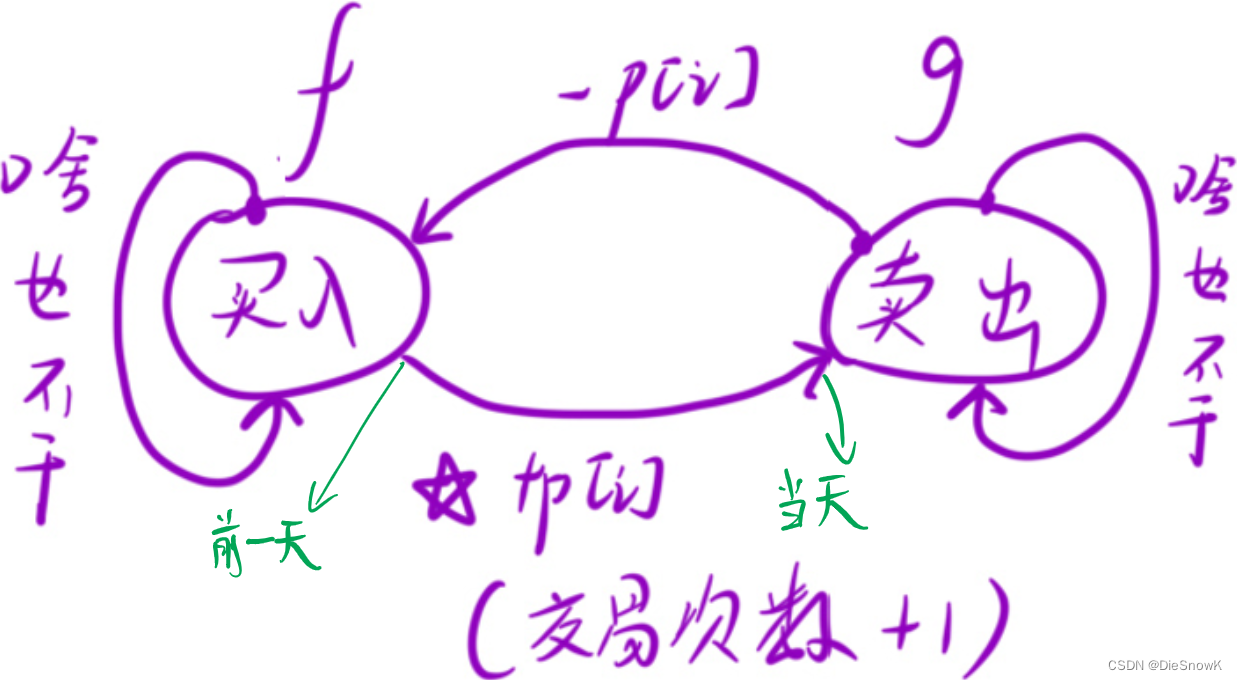
- 推导状态转移方程：本题关系复杂，可以画图辅助
  - f[i][j] = max(f[i - 1][j], g[i - 1][j] - p[i])
  - g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + p[i])
    - 初始化时，只有g需要特殊处理第一列，而f并不需要
    - 为了避免这种情况，可以将这个状态方程拆成多步，分步执行
      - g[i][j] = g[i - 1][j]
      - if(j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + p[i])
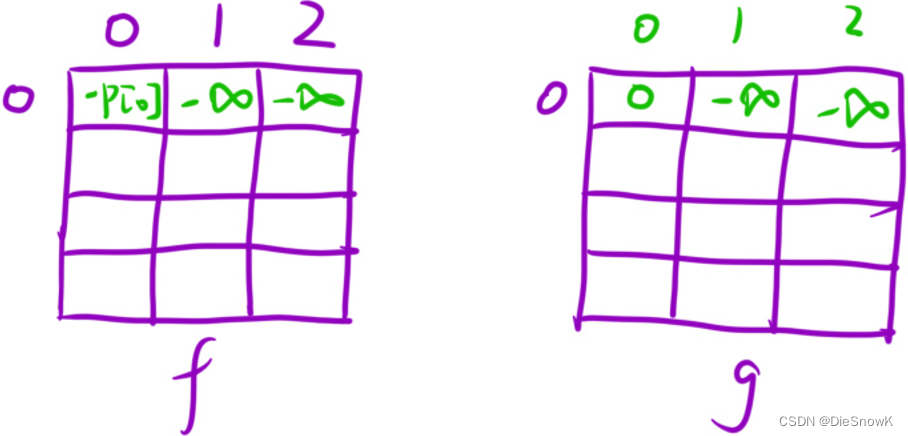
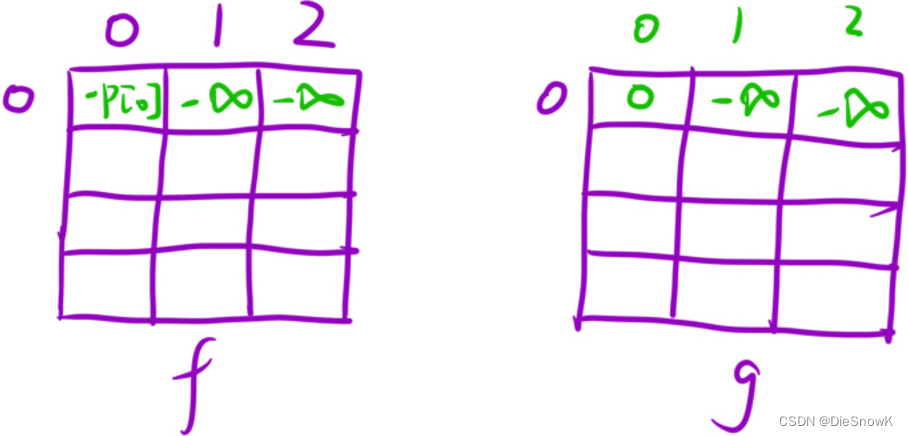
- 初始化：vector<vector<int>> dp[i][[j](n, vector<int>(3, -INF))
  - f[0][0] = -p[0], g[0][0] = 0
  - INF = 0x3f3f3f3f
  - 为什么这里用-INF而不是INT_MIN？
    - 因为本题状态方程中，有减法，可能在最开始时，对INT_MIN减一个数，此时会溢出
    - 所以选择-INF，首先它足够小，其次没有溢出风险
- 确定填表顺序：从上往下，从左往右，两个表一起填
- 确定返回值：g[n - 1]中的最大值
本题可以吸收积累的知识点：
- 算法里面初始化为无穷：INT_MAX || INT_MIN时，要注意潜在的溢出风险
  - 替换为0x3f3f3f3f || -0x3f3f3f3f即可解决该问题
  - 首先它足够大，其次它没有溢出风险
- 多个状态方程，其中只有一部分的状态方程需要特殊的初始化，那么可以想办法把这个状态方程拆成多步，分步执行，尝试避免特殊处理初始化

3.代码实现

int maxProfit(vector<int>& prices) 
{
    const int INF = -0x3f3f3f3f; // 充当"INT_MIN"的角色

    int n = prices.size();
    vector<vector<int>> f(n, vector<int>(3, INF));
    vector<vector<int>> g(n, vector<int>(3, INF));
    f[0][0] = -prices[0], g[0][0] = 0;

    for(int i = 1; i < n; i++)
    {
        for(int j = 0; j < 3; j++)
        {
            f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);

            // 处理g[i][j]时，要防止越界
            g[i][j] = g[i - 1][j];
            if(j - 1 >= 0)
            {
                g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }
    }

    int ret = 0;
    for(int j = 0; j < 3; j++)
    {
        ret = max(ret, g[n - 1][j]);
    }

    return ret;
}

2.买卖股票的最佳时机 IV

1.题目链接

买卖股票的最佳时机 IV

2.算法原理详解

注意：本题为了便于初始化，有较多细节服务于它
本题思路与买卖股票的最佳时机 III几乎一致，无非是限制次数变了
细节：可能k > n / 2，此时开空间时，会多开很多无意义的空间
- 此时k = min(k, n / 2)可以解决该问题
思路：
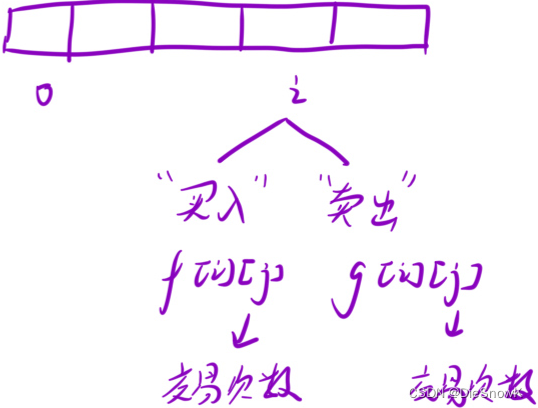
- 确定状态表示 -> dp[i]的含义
  - 第i天结束之后，所能获得的最大利润
  - 本题，状态表示还可以继续细分：
    - f[i][j]：第i天结束之后，完成了j次交易，处于“买入”状态，此时的最大利润
    - g[i][j]：第i天结束之后，完成了j次交易，处于“卖出”状态，此时的最大利润
- 推导状态转移方程：本题关系复杂，可以画图辅助
  - f[i][j] = max(f[i - 1][j], g[i - 1][j] - p[i])
  - g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + p[i])
    - 初始化时，只有g需要特殊处理第一列，而f并不需要
    - 为了避免这种情况，可以将这个状态方程拆成多步，分步执行
      - g[i][j] = g[i - 1][j]
      - if(j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + p[i])
- 初始化：vector<vector<int>> dp[i][[j](n, vector<int>(3, -INF))
  - f[0][0] = -p[0], g[0][0] = 0
  - INF = 0x3f3f3f3f
  - 为什么这里用-INF而不是INT_MIN？
    - 因为本题状态方程中，有减法，可能在最开始时，对INT_MIN减一个数，此时会溢出
    - 所以选择-INF，首先它足够小，其次没有溢出风险
- 确定填表顺序：从上往下，从左往右，两个表一起填
- 确定返回值：g[n - 1]中的最大值
本题可以吸收积累的知识点：
- 算法里面初始化为无穷：INT_MAX || INT_MIN时，要注意潜在的溢出风险
  - 替换为0x3f3f3f3f || -0x3f3f3f3f即可解决该问题
  - 首先它足够大，其次它没有溢出风险
- 多个状态方程，其中只有一部分的状态方程需要特殊的初始化，那么可以想办法把这个状态方程拆成多步，分步执行，尝试避免特殊处理初始化

3.代码实现

int maxProfit(int k, vector<int>& prices) 
{
    const int INF = -0x3f3f3f3f; // 替代"INT_MIN"的功能
    int n = prices.size();

    // 优化处理细节，避免空间浪费
    k = min(k, n / 2);

    vector<vector<int>> f(n, vector<int>(k + 1, INF));
    vector<vector<int>> g(n, vector<int>(k + 1, INF));
    f[0][0] = -prices[0], g[0][0] = 0;

    for(int i = 1; i < n; i++)
    {
        for(int j = 0; j <= k; j++)
        {
            f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);

            // 处理g时，要避免越界
            g[i][j] = g[i - 1][j];
            if(j - 1 >= 0)
            {
                g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }
    }

    int ret = 0;
    for(int i = 0; i <= k; i++)
    {
        ret = max(ret, g[n - 1][i]);
    }

    return ret;
}