生日悖论
假设一年有
n
n
n天,房间中有
k
k
k人,每个人的生日在这
n
n
n天中,服从均匀分布,两个人的生日相互独立
问至少要有多少人,才能使其中两个人生日相同的概率达到
p
p
p
解:考虑
k
≤
n
k\le n
k≤n
设
k
k
k个人生日互不相同为事件
A
A
A,则
P
(
A
)
=
n
n
n
−
1
n
⋯
n
−
k
+
1
n
P\left(A\right)=\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-k + 1}{n}
P(A)=nnnn−1⋯nn−k+1
由题意
P
(
A
)
≤
1
−
p
P\left(A\right) \le 1-p
P(A)≤1−p,由
1
+
x
≤
e
x
1+x \le e^{x}
1+x≤ex
P
(
A
)
≤
e
−
1
n
e
−
2
n
⋯
e
k
−
1
n
=
e
−
k
(
k
−
1
)
2
n
≤
1
−
p
P\left(A\right) \le e^{-\frac{1}{n}} e^{-\frac{2}{n}}\cdots e^{\frac{k-1}{n}}=e^{-\frac{k\left(k-1\right)}{2n}} \le 1-p
P(A)≤e−n1e−n2⋯enk−1=e−2nk(k−1)≤1−p
解得
k
≥
1
+
1
−
2
n
ln
(
1
−
p
)
2
k \ge \frac{1 + \sqrt{1-2n\ln\left(1-p\right)}}{2}
k≥21+1−2nln(1−p)
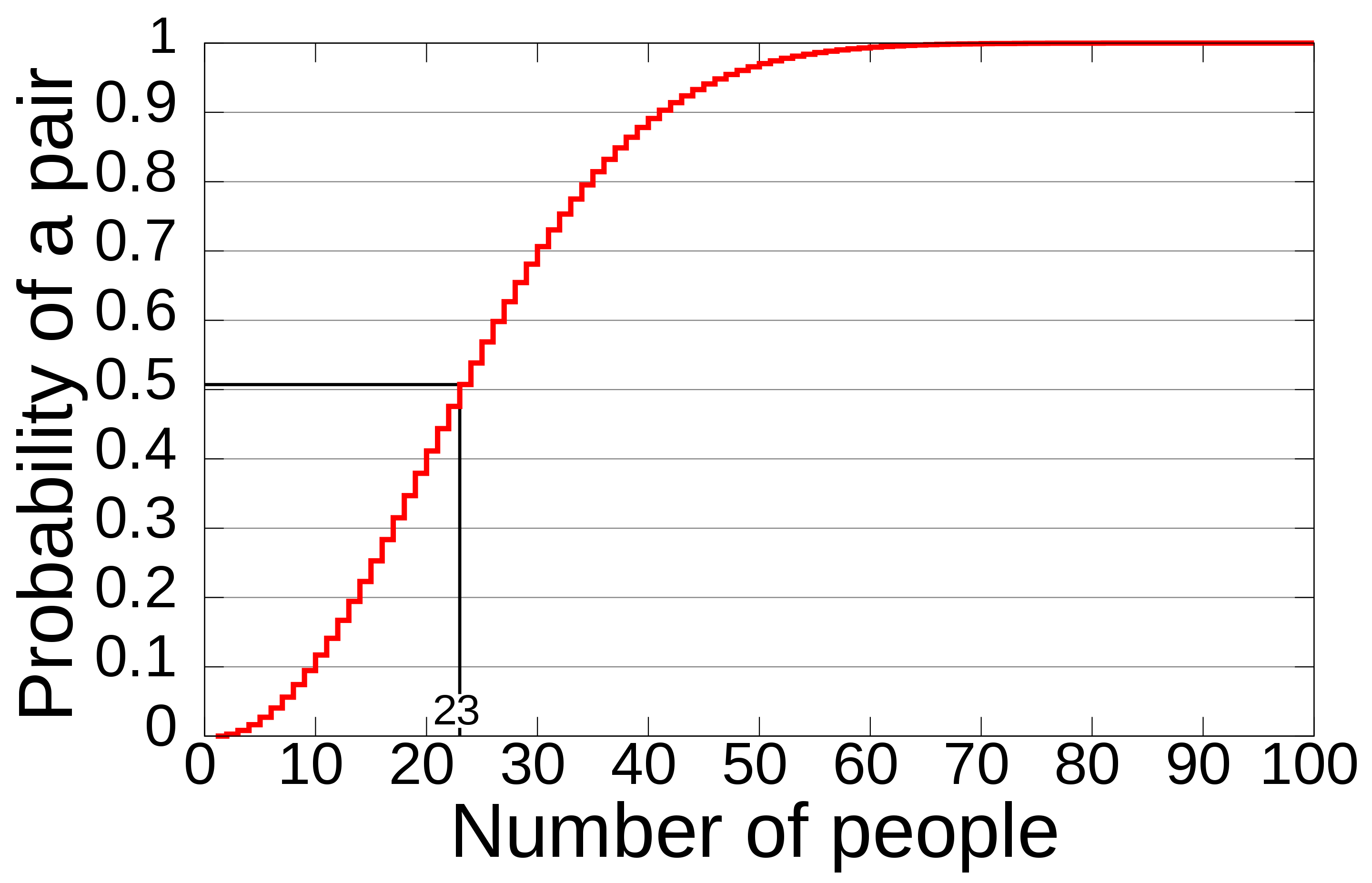
当
n
=
365
,
p
=
1
2
n=365,p=\frac{1}{2}
n=365,p=21时,
k
=
23
k=23
k=23,也就是说一个房间中至少23人就能使其中两个人生日相同的概率达到
50
%
50\%
50%
由于这个事实十分反直觉,故称为一个悖论
Pollard-Rho算法
Pollard-Rho算法是一种用于快速分解非平凡因数的算法
通过
f
(
x
)
=
(
x
2
+
c
)
m
o
d
n
f\left(x\right) = \left(x^2 + c\right) \mathop{mod} n
f(x)=(x2+c)modn来生成一个随机数序列
{
x
i
}
\left\{x_i\right\}
{xi},其中
c
c
c是一个随机数
随机取一个
x
1
x_1
x1,令
x
2
=
f
(
x
1
)
,
⋯
,
x
i
=
f
(
x
i
−
1
)
x_2=f\left(x_1\right),\cdots,x_i=f\left(x_{i-1}\right)
x2=f(x1),⋯,xi=f(xi−1),
这样产生的序列会形成一个
ρ
\rho
ρ,也就是说会产生一个环
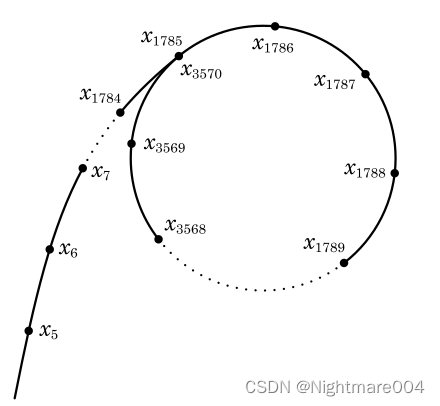
∀
k
∈
N
+
,
g
c
d
(
k
,
n
)
∣
n
\forall k \in \mathbb{N}_+, gcd\left(k,n\right)\mid n
∀k∈N+,gcd(k,n)∣n,只要选取适当的
k
k
k使得
1
<
g
c
d
(
k
,
n
)
<
n
1< gcd\left(k,n\right)<n
1<gcd(k,n)<n,就能得到一个约数
g
c
d
(
k
,
n
)
gcd\left(k,n\right)
gcd(k,n)
满足这样的条件的
k
k
k不少,
k
k
k有若干质因子,每个质因子及其倍数都是可行的
由生日悖论,伪随机数序列中不同值的数量约为
O
(
n
)
O\left(\sqrt{n}\right)
O(n)(怎么算出来的其实我也不知道 )
设
m
m
m为
n
n
n的最小非平凡因子,显然
m
≤
n
m \le \sqrt{n}
m≤n,令
y
i
=
x
i
m
o
d
m
y_i = x_i \mathop{mod} m
yi=ximodm
若
1
≤
c
<
n
1\le c < n
1≤c<n,则
y
i
+
1
=
x
i
+
1
m
o
d
m
=
(
(
x
i
2
+
c
)
m
o
d
n
)
m
o
d
m
=
(
x
i
2
+
c
)
m
o
d
m
=
(
(
x
i
m
o
d
m
)
2
+
c
)
m
o
d
m
=
(
y
i
2
+
c
)
m
o
d
m
\begin{aligned} y_{i+1} & = x_{i+1} \mathop{mod} m\\ &=\left(\left(x_i^2 +c\right)\mathop{mod} n\right)\mathop{mod}m\\ &=\left(x_i^2 + c\right)\mathop{mod}m\\ &=\left(\left(x_i \mathop{mod} m\right)^2 + c\right)\mathop{mod} m\\ &=\left(y_i^2 + c\right)\mathop{mod} m \end{aligned}
yi+1=xi+1modm=((xi2+c)modn)modm=(xi2+c)modm=((ximodm)2+c)modm=(yi2+c)modm
于是我们可以得到新的序列
{
y
i
}
\left\{y_i\right\}
{yi}并且根据生日悖论可以得知序列中不同值的个数约为
O
(
m
)
≤
O
(
n
1
4
)
O\left(\sqrt{m}\right) \le O\left(n^{\frac{1}{4}}\right)
O(m)≤O(n41)
假设存在两个位置
i
,
j
i,j
i,j,使得
x
i
≠
x
j
x_i\neq x_j
xi=xj且
y
i
=
y
j
y_i =y_j
yi=yj,则
n
∤
∣
x
i
−
x
i
∣
n \nmid \left|x_i-x_i\right|
n∤∣xi−xi∣且
m
∣
∣
x
i
−
x
j
∣
m|\left|x_i-x_j\right|
m∣∣xi−xj∣
进而
1
<
g
c
d
(
∣
x
i
−
x
j
∣
,
n
)
<
n
1<gcd\left(\left|x_i-x_j\right|, n\right)<n
1<gcd(∣xi−xj∣,n)<n
因此我们可以通过
g
c
d
(
∣
x
i
−
x
j
∣
,
n
)
gcd\left(\left|x_i-x_j\right|, n\right)
gcd(∣xi−xj∣,n)获得
n
n
n的一个非平凡因子
floyd判环
a
=
f
(
a
)
a = f(a)
a=f(a)
b
=
f
(
f
(
b
)
b=f(f(b)
b=f(f(b)
如果
a
=
b
a=b
a=b则有环,就直接返回,更换个
c
c
c再来一遍
如果
g
c
d
(
∣
a
−
b
∣
)
>
1
gcd\left(\left|a-b\right|\right)>1
gcd(∣a−b∣)>1,则得到了一个因数
洛谷P4718
__int128 + 优化gcd + 7个数字判断质数 + O2才能过(不开O2会T第13个点)
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <ctime>
using namespace std;
typedef long long LL;
LL gcd(LL x, LL y){
if (!x) return y;
if (!y) return x;
LL t = __builtin_ctzll(x | y);
x >>= __builtin_ctzll(x);
do
{
y >>= __builtin_ctzll(y);
if (x > y) swap(x, y);
y -= x;
} while (y);
return x << t;
}
LL quick_pow(LL a, LL b, LL p) {
LL res = 1;
while (b) {
if (b & 1)res = (__int128)res * a % p;
a = (__int128)a * a % p;
b >>= 1;
}
return res;
}
const LL bases[] = {2, 325, 9375, 28178, 450775, 9780504, 1795265022};
bool Rabin_Miller(LL n) {
if (n < 3 || (n & 1) == 0)return n == 2;
LL u = n - 1, t = 0;
// n - 1 = u * (2^t)
while ((u & 1) == 0) {
u >>= 1;
++t;
}
for (int i = 0; i < 7; ++i) {
LL a = bases[i] % n;
if (a == 0)continue;
LL v = quick_pow(a, u, n);
if (v == 1)continue;
LL s;
for (s = 0; s < t; ++s) {
//a^{u * 2^s}= -1 (mod n)
if (v == n - 1)break;
v = (__int128)v * v % n;
}
if (s == t)return false;
}
return true;
}
LL max_factor;
LL f(LL x, LL c, LL p) {
return ((__int128)x * x % p + c) % p;
}
LL getRandom(const LL& a, const LL& b) {
return ((1LL * rand() << 32LL) + 1LL * rand()) % (b - a + 1LL) + a;
}
LL Pollard_Rho_floyd(LL x) {
if (x == 4)return 2;
LL c = getRandom(3, x - 1);//[3,x-1]
LL s = getRandom(0, x - 1);//[0,x-1]
s = f(s, c, x);
LL t = f(s, c, x);
while (s != t) {
LL d = gcd(abs(t - s), x);
if (d > 1)return d;
s = f(s, c, x);
t = f(f(t, c, x), c, x);
}
return x;
}
void fac(LL x) {
if (x <= max_factor || x < 2)return;
if (Rabin_Miller(x)) {// x是质数
if (x > max_factor) {
max_factor = x;
}
return;
}
LL p = x;
while (p >= x)p = Pollard_Rho_floyd(x);//找一个因子p
while (x % p == 0)x /= p;
fac(x);
fac(p);
}
int main() {
srand((unsigned)time(NULL));
int T;
scanf("%d", &T);
while (T--) {
max_factor = 1;
LL n;
scanf("%lld", &n);
fac(n);
if (n == max_factor)printf("Prime\n");
else printf("%lld\n", max_factor);
}
return 0;
}
倍增优化
由于频繁使用gcd会导致复杂度上去,
我们考虑累积几次再算gcd
下面是
m
i
n
(
2
k
−
1
,
128
)
min\left(2^k -1, 128\right)
min(2k−1,128)次算一个gcd
洛谷P4718
__int128
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <ctime>
using namespace std;
typedef long long LL;
LL gcd(LL a, LL b){
LL c;
while (b){
c = a % b;
a = b;
b =c;
}
return a;
}
LL quick_pow(LL a, LL b, LL p) {
LL res = 1;
while (b) {
if (b & 1)res = (__int128)res * a % p;
a = (__int128)a * a % p;
b >>= 1;
}
return res;
}
const LL bases[] = {2, 325, 9375, 28178, 450775, 9780504, 1795265022};
bool Rabin_Miller(LL n) {
if (n < 3 || (n & 1) == 0)return n == 2;
LL u = n - 1, t = 0;
// n - 1 = u * (2^t)
while ((u & 1) == 0) {
u >>= 1;
++t;
}
for (int i = 0; i < 7; ++i) {
LL a = bases[i] % n;
if (a == 0)continue;
LL v = quick_pow(a, u, n);
if (v == 1)continue;
LL s;
for (s = 0; s < t; ++s) {
//a^{u * 2^s}= -1 (mod n)
if (v == n - 1)break;
v = (__int128)v * v % n;
}
if (s == t)return false;
}
return true;
}
LL max_factor;
LL f(LL x, LL c, LL p) {
return ((__int128)x * x % p + c) % p;
}
LL getRandom(const LL& a, const LL& b) {
return ((1LL * rand() << 32LL) + 1LL * rand()) % (b - a + 1LL) + a;
}
LL Pollard_Rho(LL x) {
if (x == 4)return 2;
LL c = getRandom(3, x - 1);//[3,x-1]
LL s = getRandom(0, x - 1);//[0,x-1]
s = f(s, c, x);
LL t = f(s, c, x);
for (int lim = 1; s != t; lim = std::min(128, lim << 1)) {
LL val = 1;
for (int i = 0; i < lim; ++i) {
LL temp = (__int128)val * abs(s-t) % x;
if (temp == 0)break;
val = temp;
s = f(s, c, x);
t = f(f(t, c, x), c, x);
}
LL d = gcd(val, x);
if (d > 1)return d;
}
return x;
}
void fac(LL x) {
if (x <= max_factor || x < 2)return;
if (Rabin_Miller(x)) {// x是质数
if (x > max_factor) {
max_factor = x;
}
return;
}
LL p = x;
while (p >= x)p = Pollard_Rho(x);//找一个因子p
while (x % p == 0)x /= p;
fac(x);
fac(p);
}
int main() {
srand((unsigned)time(NULL));
int T;
scanf("%d", &T);
while (T--) {
max_factor = 1;
LL n;
scanf("%lld", &n);
fac(n);
if (n == max_factor)printf("Prime\n");
else printf("%lld\n", max_factor);
}
return 0;
}