详解MySQL数据库索引实现机制 - B树和B+树
- 1.索引的出现
- 2.hash算法的缺点
- 3.二叉排序树BST
- 4.平衡二叉树AVL
- 5.红黑树
- 6.B树诞生了
- 7.B+树
1.索引的出现
索引是一种用于快速查询和检索数据的数据结构,其本质可以看成是一种排序好的数据结构。
索引的作用就相当于书的目录。打个比方: 我们在查字典的时候,如果没有目录,那我们就只能一页一页的去找我们需要查的那个字,速度很慢。如果有目录了,我们只需要先去目录里查找字的位置,然后直接翻到那一页就行了。
在 MySQL 中,无论是 Innodb 还是 MyIsam,都使用了 B+树作为索引结构☹️
2.hash算法的缺点
基于索引的设计,其实有很多思路,比如最早期使用的数组查找,这种方法效率极低
后来针对数组的缺点改进使用了hash算法,但是我们发现,hash算法对于等值查询可以,但是遇到范围查询,得挨个遍历,hash就不合适了
试想一种情况:
SELECT * FROM tb1 WHERE id < 500;
Hash 索引是根据 hash 算法来定位的,难不成还要把 1 - 499 的数据,每个都进行一次 hash 计算来定位吗?这就是 Hash 最大的缺点了。
3.二叉排序树BST
终于我们找到了实现索引最好的方法,那就是:树
如果我们想基于树进行索引查找,首先普通的二叉树肯定是不行的,所以我们引入一种二叉排序树BST
BST插入数据的时候得有序,必须保证:
- 若左子树不为空,则左子树上所有结点的值都小于根结点的值
- 若右子树不为空,则右子树上所有结点的值都大于根结点的值
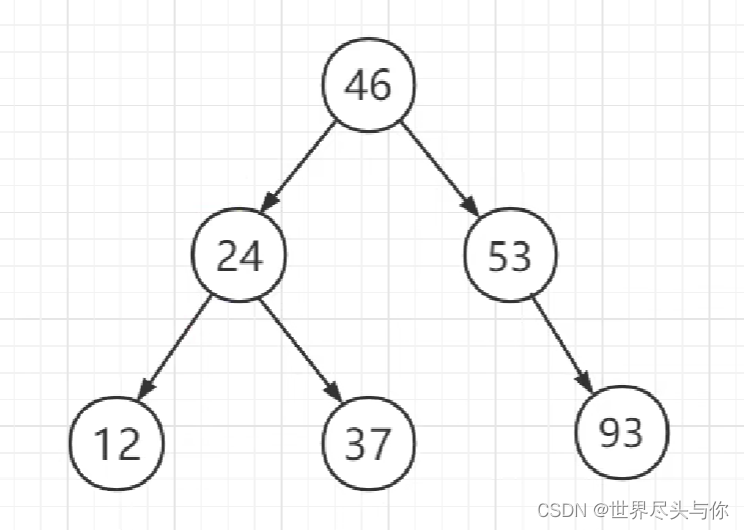
这样,查找的算法时间复杂度就变为了LogN级别
但是,请试想如果一组数据的树组成了这样的结果:
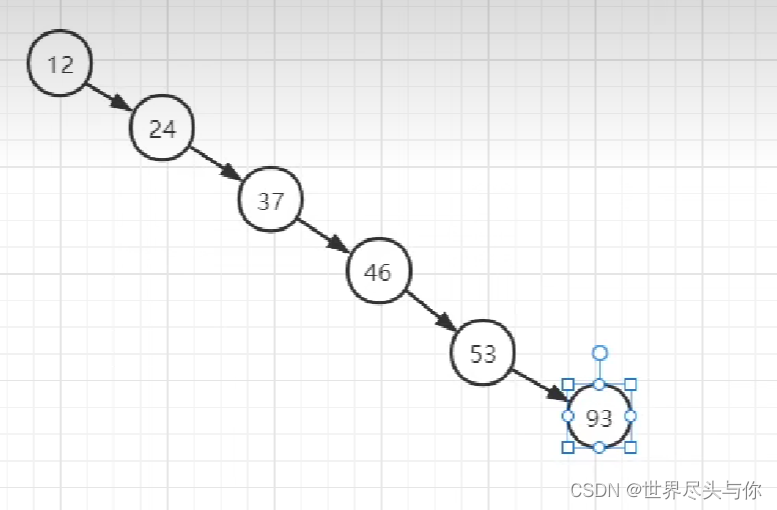
很遗憾,查询的效率又退回到了LogN级别,针对于这种致命的缺点,我们又改进了索引的算法,那就是大名鼎鼎的平衡二叉树AVL!
4.平衡二叉树AVL
AVL算法可以保证插入数据的时候得保持二叉排序树平衡
左子树和右子树高度之差的绝对值不大于1🙁
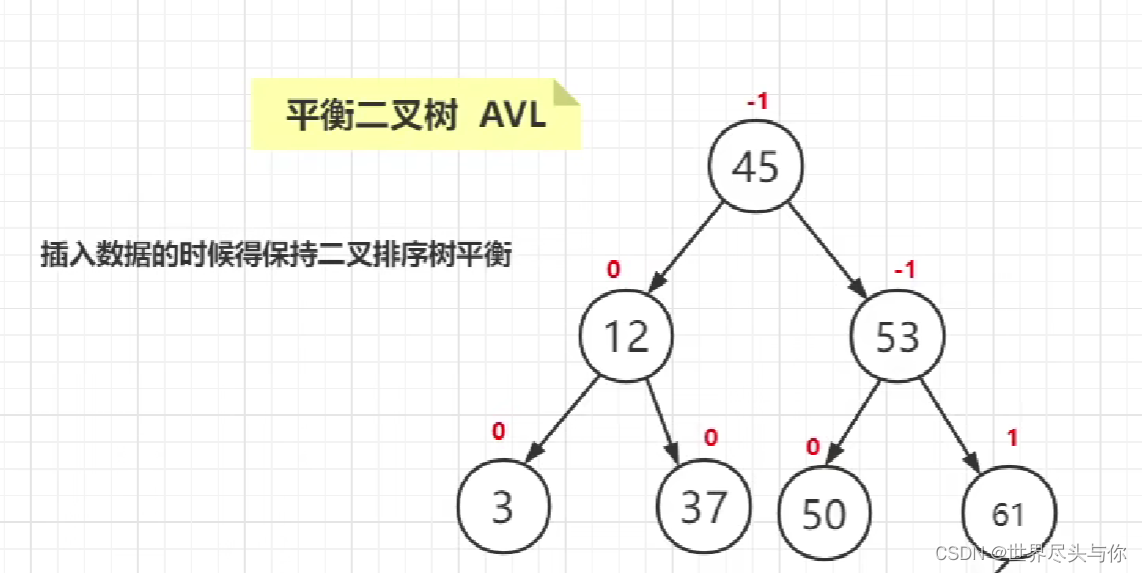
这种算法的本质是用插入的成本来弥补查询的效率,适用于插入情况特别少,但是查询情况特别多的数据!
但是一且出现,插入操作比查询操作多的情况下,AVL算法就不合适了!所以我们继续尝试改进,就引入了神秘莫测的红黑树!
5.红黑树
红黑树规定:最长子树不超过最短子树的2倍即可,这样可以极大的减少插入数据的算法开销
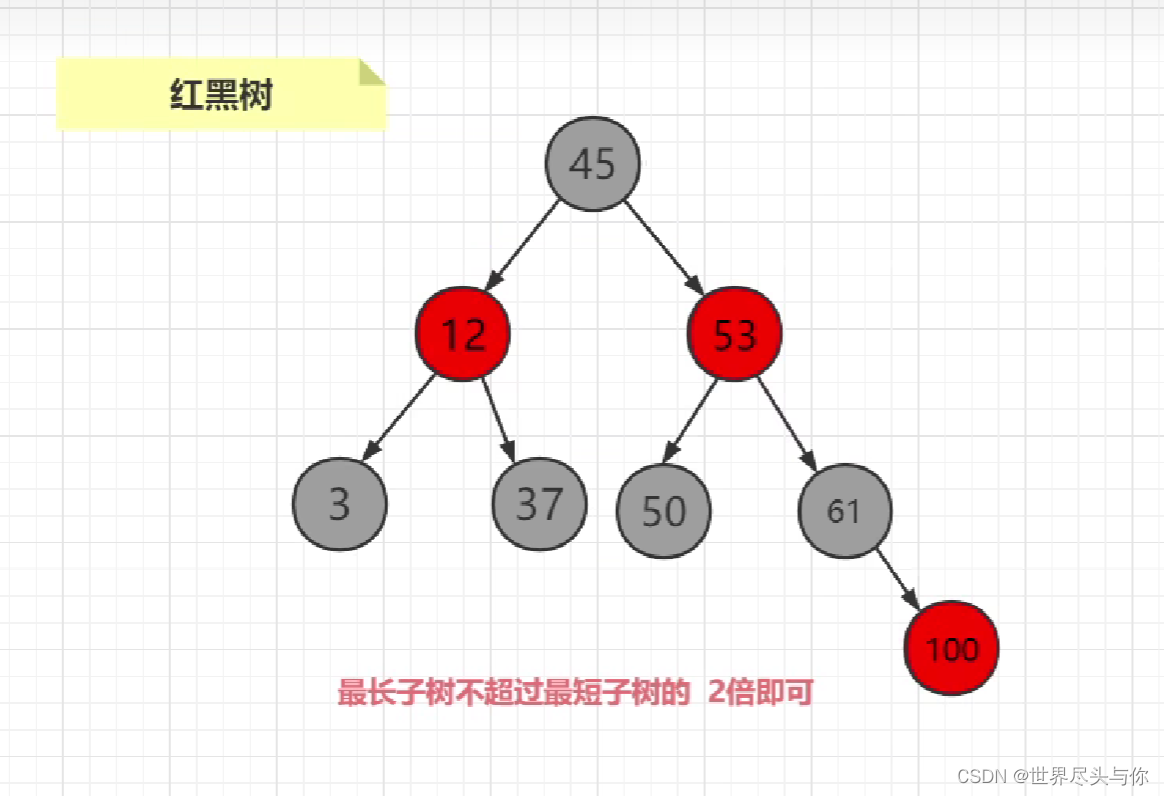
但是其实对于红黑树作为索引实现机制也有着一定的问题:随着数据的插入,发现树的深度会变深(海量数据的情况下),意味着IO次数越多,影响读取的效率
那么如何针对红黑树再做改进呢?这时有大佬发现,红黑树深度变深的本质是这是一颗二叉树,而二叉树会随着数据量的增大很快的进行递增深度,那么如果这是一颗多叉的树,这个问题不就迎刃而解了吗?于是B树诞生了!
传统二叉树:
B树:
6.B树诞生了
B树就是一个有序的多路平衡查询树😖
m叉树的结构:
- 树中每个结点至多有m个孩子结点(即至多有m-1个关键字)
- 每个节点的结构为
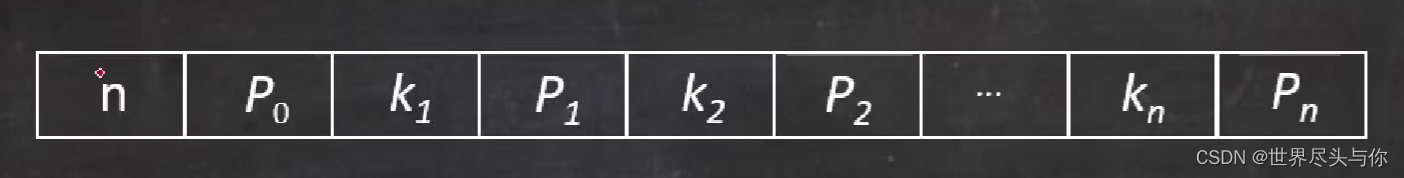
其中n表示当前节点的孩子节点的个数,Px表示第x个孩子节点的指针地址,Kx表示第x个关键字(关键字是用来判断子节点的区间的) - 除根节点外,其他结点至少有
m/2个孩子结点 - 若根节点不是叶子结点,则根结点至少有两个孩子结点
- 所有叶子结点都在同一层上,即树是所有结点的平衡因子均等于0的多路查找树
例:m=4的4阶B树
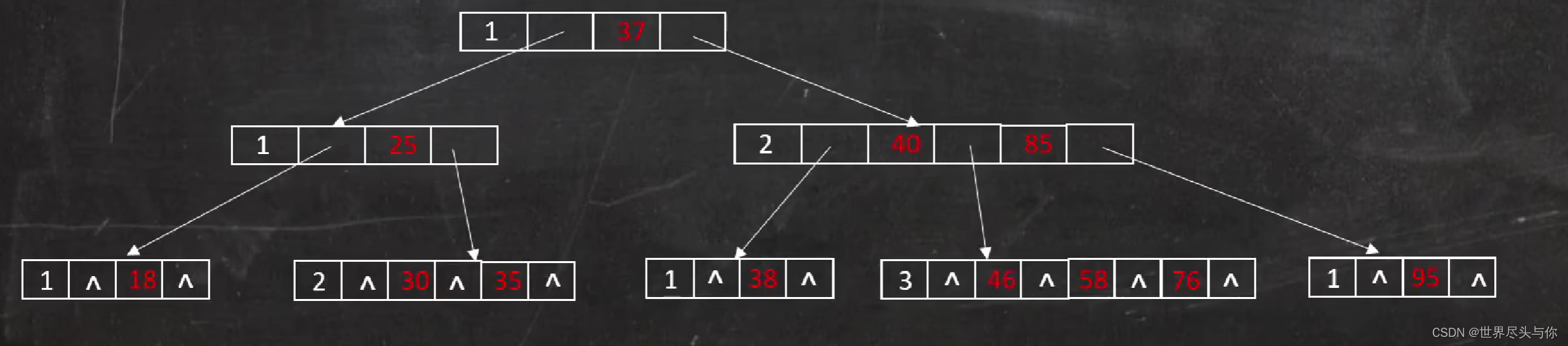
但是诸位思考,这种索引检索方式是否依然存在着一些问题呢?
B树中每个节点都可以存放表的行记录数据,每个节点的读取可以视为一次I/O读取,树的高度表示最多的I/O次数,在相同数量的总记录个数下,每个节点的记录个数越多,高度越低,查询所需的I/O次数越少
在MySQL中一个innodb页就是一个B+树节点,而一个innodb页默认为16kb大小,请试想一下如果我们把数据库的行具体的数据都存到各个节点中,势必会导致树的深度很大,这样就又产生了类似红黑树的性能瓶颈问题!
于是各位大佬们就又产生了一个想法,是否我们可以这样解决B树的缺陷:在B树只有叶子节点存放 key 和 data,其他内节点只存放 key 的值,减少内节点每个节点的空间占用,这样每个节点就可以存放更多的记录数了!这就解决方法就是数据库索引的终极解决方案:B+树!
7.B+树
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用😞
一般情况下一个两层的B+树可以存2000万行左右的数据,然后通过利用B+树叶子节点存储了所有数据并且进行了排序,并且叶子节点之间有指针,可以很好的支持全表扫描,范围查找等SQL语句