拿捏数据结构-top

top_k问题时间复杂度的计算

这里提前说明，时间复杂度的计算的目的是来计算向上调整的更优还是向下调整更优，从肉眼看的话向下调整优于向上调整，接下来我们进行时间复杂度的计算。

此时我们会用到等比数列求和以及裂项相消

如图

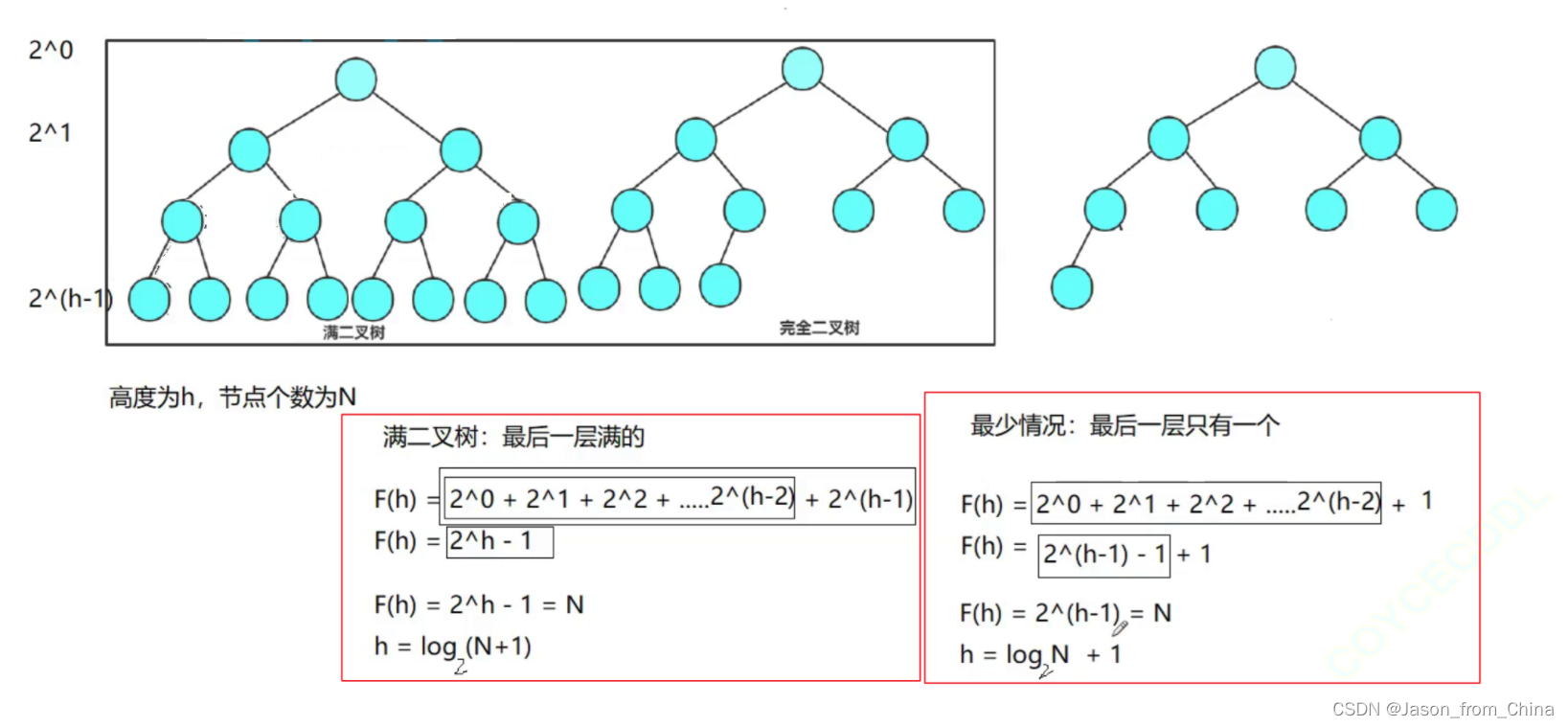
首先我们假设求的是满二叉树，我们求节点的个数

满二叉树节点个数

建堆问题：

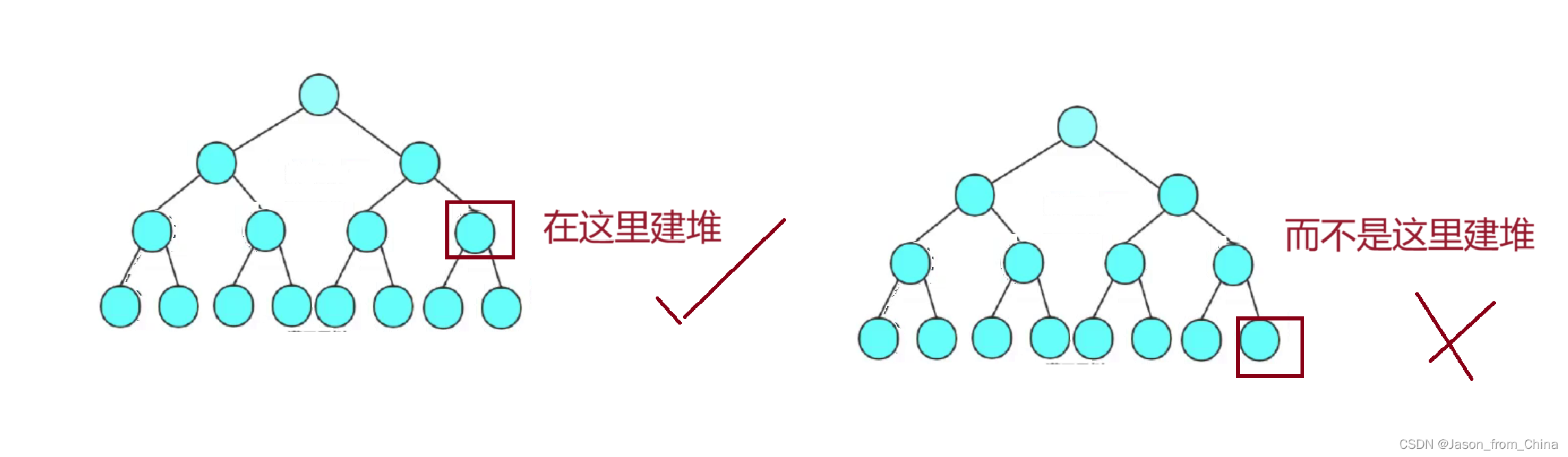
建堆的话往往的倒数第一个非叶子结点建堆，会时间复杂度最优解：也就是

在构建堆（尤其是二叉堆）时，从最后一个非叶子节点开始进行调整是时间复杂度最优解的原因是，这种方法可以减少不必要的调整操作。

为什么从最后一个非叶子节点开始？

叶子节点：在完全二叉树中，叶子节点不包含任何子节点，因此不需要进行调整。

非叶子节点：从最后一个非叶子节点开始，向上逐个进行调整，可以确保每个节点在调整时，其子树已经是堆结构。这样可以减少调整的深度，因为每个节点最多只需要与其子节点交换一次。

减少调整次数：如果从根节点开始调整，那么每个节点可能需要多次调整才能达到堆的性质，特别是那些位于树底部的节点。而从底部开始，每个节点只需要调整一次即可。

时间复杂度分析

构建堆的过程涉及对每个非叶子节点进行调整。对于一个具有 𝑛n 个节点的完全二叉树：

叶子节点：有 ⌈𝑛/2⌉⌈n/2⌉ 个叶子节点，它们不需要调整。

非叶子节点：有 ⌊𝑛/2⌋⌊n/2⌋ 个非叶子节点，需要进行调整。

对于非叶子节点，从最后一个非叶子节点开始向上调整，每个节点最多只需要进行 log⁡𝑘logk（𝑘k 是节点的深度）次交换。但是，由于树的结构，底部的节点不需要进行多次交换，因此整个调整过程的时间复杂度比 𝑂(𝑛log⁡𝑛)O(nlogn) 要低。

实际上，构建堆的时间复杂度是 𝑂(𝑛)O(n)，这是因为：

从最后一个非叶子节点开始，每个节点的调整次数与其深度成反比。

根节点的调整次数最多，但只需要一次。

越往下，节点的深度越小，但需要调整的节点数量越多。

总结

从最后一个非叶子节点开始建堆，可以确保每个节点的调整次数与其深度成反比，从而减少总的调整次数。这种方法利用了完全二叉树的性质，使得整个建堆过程的时间复杂度达到最优，即 𝑂(𝑛)O(n)。这是构建堆的最优策略，因为它最小化了必要的调整操作，从而提高了算法的效率。

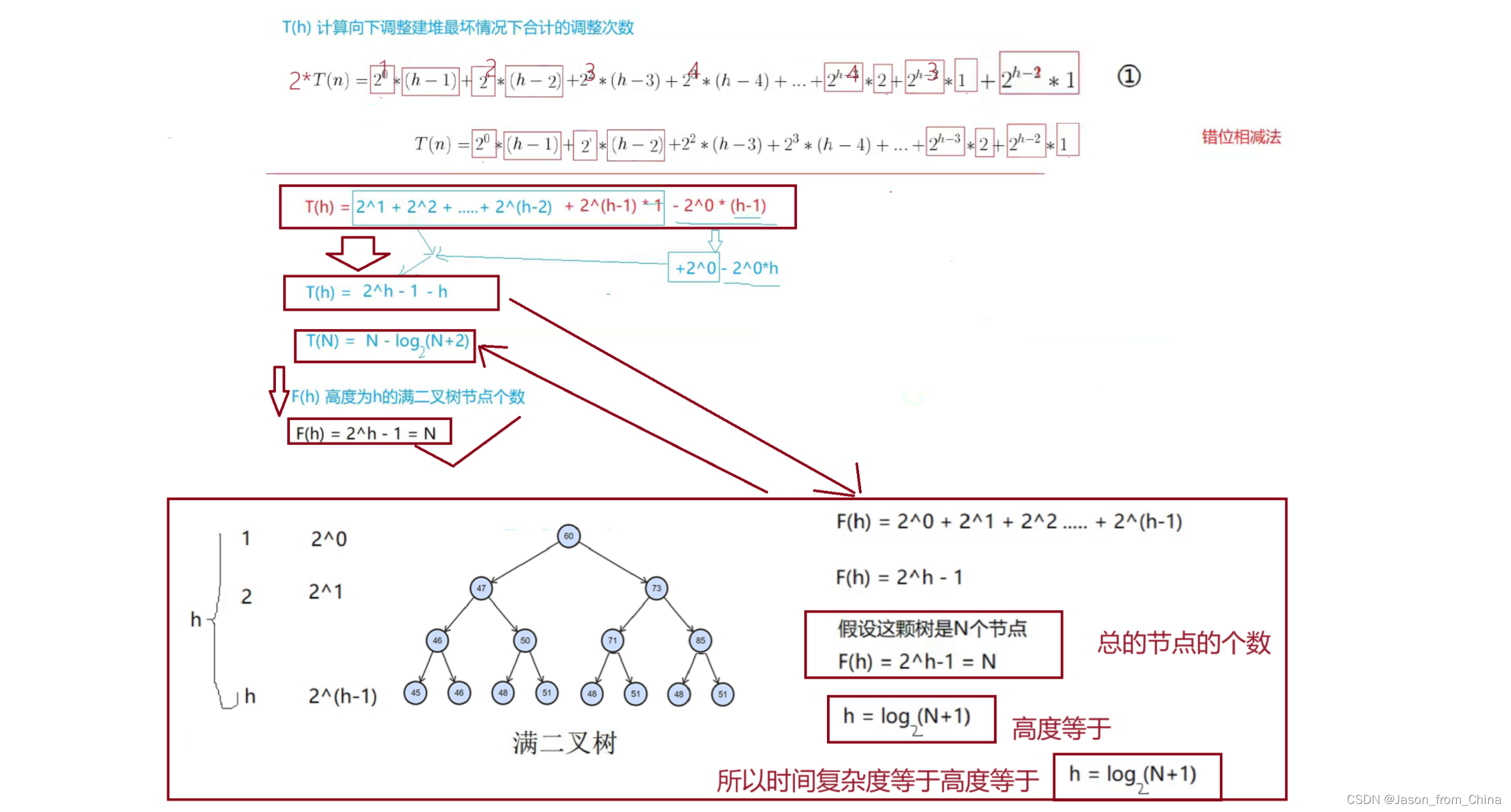
建堆复杂度讲解：（向下调整建堆计算）

如图：

这里为什么-2呢，因为我们的向下调整只是调整h-1层，第h层的节点的个数是2^h-1，所以第h-1层自然就是-2

所以我们发现，建堆的时候我们h-1高度的节点的个数相加得出的结果

为T(n)

所以我们进行计算

从而得出时间复杂度，为什么时间复杂度是高度，因为向下调整的时候，我们循环终止条件是循环的高度，也就是当父亲节点不小于sz的时候，所以计算出高度也就计算出了时间复杂度

建堆复杂度讲解：（向上调整建堆计算）

如图：

计算图解

所以我们得出结论，这里多了n次

对比

向上调整（AdjustUp）和向下调整（AdjustDown）的时间复杂度通常与堆的高度相关，即 log⁡𝑘logk，其中 𝑘k 是堆中元素的数量。然而，在特定情况下，特别是在构建堆的过程中，这些操作的总时间复杂度可以是 𝑂(𝑛)O(n)，这里的 𝑛n 是堆中元素的数量。

单个操作的时间复杂度：

向上调整 (AdjustUp)：对于单个元素，向上调整的时间复杂度是 𝑂(log⁡𝑘)O(logk)，因为它可能需要从叶子节点一直调整到根节点，最多涉及 log⁡𝑘logk 层的比较和交换。

向下调整 (AdjustDown)：同样，对于单个元素，向下调整的时间复杂度也是 𝑂(log⁡𝑘)O(logk)，因为它可能需要从根节点调整到叶子节点，同样最多涉及 log⁡𝑘logk 层的比较和交换。

构建堆的总时间复杂度：

当我们讨论构建一个包含 𝑛n 个元素的堆时，所有元素的向上调整操作的总时间复杂度是 𝑂(𝑛)O(n)。这是因为：

树的非叶子节点大约是 𝑛/2n/2（因为叶子节点也是 𝑛/2n/2 左右）。

每个非叶子节点的调整操作最多涉及 log⁡𝑘logk 的时间，但是由于树的结构，从根到叶的路径上的节点数量总和大致是 𝑛n。

因此，所有节点的向上调整操作加起来的时间复杂度是 𝑂(𝑛)O(n)。

为什么是 𝑂(𝑛)O(n) 而不是 𝑂(𝑛log⁡𝑘)O(nlogk)？

树的结构特性：在完全二叉树中，每个层级的节点数量是指数增长的。从根节点（1个节点）到第二层（2个节点），再到第三层（4个节点），等等。因此，较低层级的节点数量远多于较高层级的节点数量。

调整深度：根节点的调整可能需要 log⁡𝑘logk 的时间，但较低层级的节点只需要较少的调整时间。由于底部层级的节点数量较多，它们较短的调整时间在总体上对总时间复杂度的贡献较小。

总结：

对于单个元素，向上调整和向下调整的时间复杂度是 𝑂(log⁡𝑘)O(logk)。

在构建堆的过程中，所有元素的向上调整操作的总时间复杂度是 𝑂(𝑛)O(n)，而不是 𝑂(𝑛log⁡𝑘)O(nlogk)，这是由于完全二叉树的结构特性和调整操作的分布。

因此，向上调整和向下调整在构建堆的过程中的总时间复杂度是 𝑂(𝑛)O(n)，而不是 𝑂(log⁡𝑛)O(logn)。这个线性时间复杂度是构建堆算法的一个重要特性，使得它在处理大量数据时非常高效。

向上调整和向下调整虽然最后计算的都是O(N)

但是满二叉树最后一层占据一半的节点

所以我们得出结论，向下调整的复杂度优于向上调整的复杂度

top_k问题的实现逻辑

1，首先我们创建一个文件，写入随机数值1000w个

2，如果需要读取文件里面最大的10个数值，那么我们就需要，创建一个小堆

原因：

这样的话，输入数值的时候，如果读取的数值比堆顶大，就会替换堆顶从而进堆，然后进行堆排序。

3，在读取文件的时候，我们需要读取一个接收一个，然后进行数值的对比，从而进行交换。

4，最后打印最大的数值

5，备注：我们如何判断我们的找到的最大的前十个数值的正确的，

也是很简单的，我们设定的随机数值是10000以内的，然后设定完之后，我们不调用，进入TXT里面更改一些数值。设定一些大于一万的数值，此时我们就可以发现我们筛选的数值对不对。

当然如果我们需要找最小的数值，那么我们设定数值最好为-1，因为十万个数值，很可能是有很多0的。但是我们肉眼看不出来。

top_k计算的代码实现

//进行计算
void TOP_K()
{
	int k = 10;
	//scanf("%d", &k);
	FILE* ps = fopen("data.txt", "r");
	if (ps == NULL)
	{
		perror("Error:opening:file");
		exit(1);
	}
	//创建空间存储
	int* tmp = (int*)malloc(sizeof(int) * k);
	if (tmp == NULL)
	{
		perror("TOP_K():Heap* tmp:error");
		exit(1);
	}
	//读取个数
	for (int i = 0; i < 10; i++)
	{
		fscanf(ps, "%d", &tmp[i]);
	}
	// 建堆,从最后一个非叶子节点开始建堆,
	// 这里的 -1-1 实际上看起来像是一个错误。
	// 通常，当我们需要找到最后一个非叶子节点的索引以开始建堆过程时，我们会从倒数第二个节点开始（因为数组索引从0开始）。对于大小为 k 的数组，最后一个非叶子节点的索引计算如下：
	// 简单的说就是，k是数值，我们需要传参传递是下标，找到父亲节点需要减去1 除以2 所以就有了-2的情况
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(tmp, k, i);
	}
	//排序
	int val = 0;
	int ret = fscanf(ps, "%d", &val);
	while (ret != EOF)
	{
		if (tmp[0] < val)
		{
			tmp[0] = val;
			AdjustDown(tmp, k, 0);
		}
		ret = fscanf(ps, "%d", &val);
	}

	//打印
	for (int i = 0; i < k; i++)
	{
		printf("%d ", tmp[i]);
	}
	fclose(ps);

}

top_k完整代码

//TOP_K问题的实现 小堆寻找最大值
//创建随机数值
void TOP_K_fopen_w()
{
	FILE* ps = fopen("data.txt", "w");
	if (ps == NULL)
	{
		perror("FILE* ps :fopen:error");
		exit(1);
	}
	srand(time(0));
	for (int i = 0; i < 100000; i++)
	{
		int s = rand() % 10000;
		fprintf(ps, "%d\n", s);
	}

	fclose(ps);
}
//进行计算
void TOP_K()
{
	int k = 10;
	//scanf("%d", &k);
	FILE* ps = fopen("data.txt", "r");
	if (ps == NULL)
	{
		perror("Error:opening:file");
		exit(1);
	}
	//创建空间存储
	int* tmp = (int*)malloc(sizeof(int) * k);
	if (tmp == NULL)
	{
		perror("TOP_K():Heap* tmp:error");
		exit(1);
	}
	//读取个数
	for (int i = 0; i < 10; i++)
	{
		fscanf(ps, "%d", &tmp[i]);
	}
	// 建堆,从最后一个非叶子节点开始建堆,
	// 这里的 -1-1 实际上看起来像是一个错误。
	// 通常，当我们需要找到最后一个非叶子节点的索引以开始建堆过程时，我们会从倒数第二个节点开始（因为数组索引从0开始）。对于大小为 k 的数组，最后一个非叶子节点的索引计算如下：
	// 简单的说就是，k是数值，我们需要传参传递是下标，找到父亲节点需要减去1 除以2 所以就有了-2的情况
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(tmp, k, i);
	}
	//排序
	int val = 0;
	int ret = fscanf(ps, "%d", &val);
	while (ret != EOF)
	{
		if (tmp[0] < val)
		{
			tmp[0] = val;
			AdjustDown(tmp, k, 0);
		}
		ret = fscanf(ps, "%d", &val);
	}

	//打印
	for (int i = 0; i < k; i++)
	{
		printf("%d ", tmp[i]);
	}
	fclose(ps);

}