均值算法详细教程（个人总结版）

news2024/12/24 8:10:39

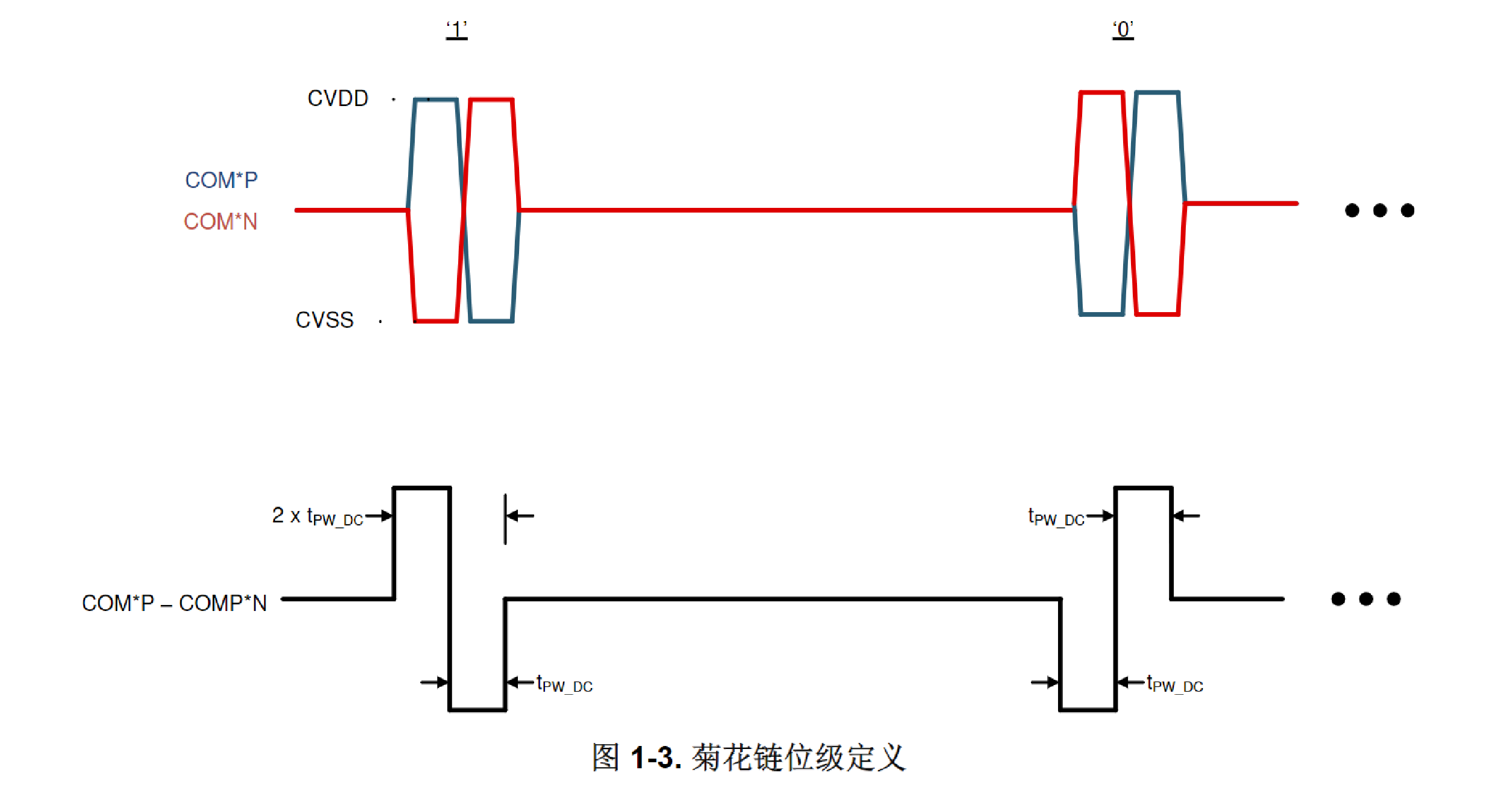
背景

均值算法，也称为平均值算法，是统计分析中的基本方法之一。它通过求取一组数据的平均值来概括数据的集中趋势。在数据分析、机器学习、信号处理等领域，均值算法被广泛应用。

均值的种类

算术均值（Arithmetic Mean）：最常见的均值算法，即所有数据点的和除以数据点的数量。
几何均值（Geometric Mean）：用于处理比例数据或成倍增长的数据。
调和均值（Harmonic Mean）：常用于处理速度等倒数关系的数据。
加权均值（Weighted Mean）：用于处理不同数据点有不同权重的情况。

算术均值

算术均值是最简单和最常见的均值类型，用于许多基本统计分析。它计算一组数据的和，然后除以数据点的数量。

算法描述

算术均值的计算公式为：算术均值=

其中，xi 是数据点，n 是数据点的数量。

算术均值的优缺点

优点：

简单易懂，计算方便。
能够很好地反映数据的集中趋势。

缺点：

对极端值（离群点）敏感，容易受到它们的影响。

算术均值算法实现

Python代码示例

def arithmetic_mean(data):
    if len(data) == 0:
        return 0
    return sum(data) / len(data)

# 示例数据
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
mean = arithmetic_mean(data)
print("算术均值:", mean)

几何均值

几何均值用于处理比例数据或成倍增长的数据，它将所有数据点相乘，然后取 �n 次方根。

算法描述

几何均值的计算公式为：几何均值=

几何均值的优缺点

优点：

对数变换数据时，几何均值能够更好地反映数据的趋势。
不容易受到极端值的影响。

缺点：

计算复杂度较高。
不能处理包含零或负数的数据。

几何均值算法实现

Python代码示例

import math

def geometric_mean(data):
    if len(data) == 0:
        return 0
    product = 1
    for num in data:
        product *= num
    return product ** (1 / len(data))

# 示例数据
data = [1, 2, 3, 4, 5]
mean = geometric_mean(data)
print("几何均值:", mean)

调和均值

调和均值常用于处理速度等倒数关系的数据，它是倒数均值的倒数。

算法描述

调和均值的计算公式为：调和均值=�∑�=1�1��调和均值=∑i=1nxi1n

调和均值的优缺点

优点：

对数据中小值更加敏感，适用于计算平均速度等。

缺点：

不能处理包含零的数据。

调和均值算法实现

Python代码示例

def harmonic_mean(data):
    if len(data) == 0:
        return 0
    reciprocal_sum = 0
    for num in data:
        reciprocal_sum += 1 / num
    return len(data) / reciprocal_sum

# 示例数据
data = [1, 2, 3, 4, 5]
mean = harmonic_mean(data)
print("调和均值:", mean)

加权均值

加权均值用于处理不同数据点有不同权重的情况，它考虑了每个数据点的重要性。

算法描述

加权均值的计算公式为：加权均值=

其中，wi 是权重。

加权均值的优缺点

优点：

考虑了数据点的权重，能更准确地反映数据的实际情况。

缺点：

需要额外的权重信息。

加权均值算法实现

Python代码示例

def weighted_mean(data, weights):
    if len(data) != len(weights) or len(data) == 0:
        return 0
    weighted_sum = 0
    weight_sum = 0
    for i in range(len(data)):
        weighted_sum += data[i] * weights[i]
        weight_sum += weights[i]
    return weighted_sum / weight_sum

# 示例数据
data = [1, 2, 3, 4, 5]
weights = [0.1, 0.2, 0.3, 0.4, 0.5]
mean = weighted_mean(data, weights)
print("加权均值:", mean)

算术均值、几何均值、调和均值与加权均值对比

示例数据对比

data = [1, 2, 3, 4, 5]

arithmetic_mean_result = arithmetic_mean(data)
geometric_mean_result = geometric_mean(data)
harmonic_mean_result = harmonic_mean(data)
weighted_mean_result = weighted_mean(data, [1, 1, 1, 1, 1])

print("算术均值:", arithmetic_mean_result)
print("几何均值:", geometric_mean_result)
print("调和均值:", harmonic_mean_result)
print("加权均值（等权重）:", weighted_mean_result)