在机器学习的广阔领域中，矩阵对角化作为一种重要的数学工具，扮演着不可或缺的角色。从基础的线性代数理论到复杂的机器学习算法，矩阵对角化都在其中发挥着重要的作用。

矩阵对角化的概念与原理

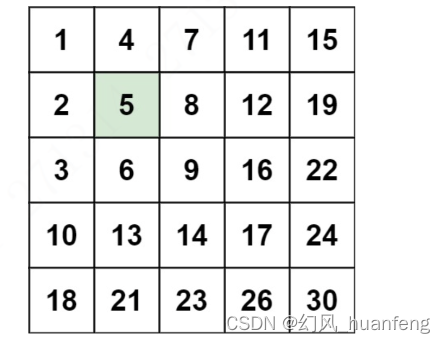
矩阵对角化是矩阵理论中的一个基本概念，也是矩阵分析和计算中的重要内容之一。具体地说，对于一个给定的n阶方阵A，如果存在一个可逆矩阵P，使得P^(-1)AP是一个对角矩阵，则称A可对角化。对角矩阵的特点是只有对角线上的元素为非零值，其余元素均为零。

矩阵对角化的重要性在于它可以简化矩阵的分析和计算。通过矩阵对角化，我们可以将原来的矩阵问题转化为对特征值的求解问题，从而更容易地得到矩阵的性质和特性。这种转换过程在数学上称为“相似变换”，即存在一个可逆矩阵P，使得A和P^(-1)AP在某种意义上是“相似”的。

矩阵对角化在机器学习中的应用

1. 特征提取与降维

在机器学习中，特征提取和降维是常见的预处理步骤。矩阵对角化可以作为一种有效的特征提取和降维方法。具体来说，对于给定的数据集，我们可以将其表示为一个矩阵X。通过对X进行矩阵对角化，我们可以得到一组新的特征向量（即对角矩阵的对角线元素），这些特征向量在某种意义上是原始数据集的“本质”或“核心”特征。这种特征提取方法不仅可以有效地降低数据的维度，还可以提高后续机器学习算法的效率和准确性。

例如，在主成分分析（PCA）中，我们利用协方差矩阵（一种特殊的实对称矩阵）的相似对角化来提取数据的主要成分或特征。通过计算协方差矩阵的特征值和特征向量，我们可以选择其中最重要的几个特征向量来构建新的特征空间，从而实现对原始数据的降维和特征提取。

1. 优化算法与梯度下降

在机器学习中，优化算法和梯度下降是训练模型的关键步骤。矩阵对角化可以在这些算法中发挥重要作用。具体来说，对于某些优化问题（如最小二乘法问题），我们可以通过将目标函数表示为矩阵形式并利用矩阵对角化的性质来简化问题的求解过程。此外，在梯度下降算法中，我们也可以利用矩阵对角化来加速算法的收敛速度。

例如，在神经网络训练中，我们经常使用梯度下降算法来优化模型的参数。然而，当模型的参数空间非常大时（如深度学习模型中的参数数量），梯度下降算法的收敛速度可能会非常慢。此时，我们可以利用矩阵对角化来近似计算Hessian矩阵（即目标函数的二阶导数矩阵）的逆矩阵，从而得到一个更加有效的优化方向并加速算法的收敛速度。

1. 聚类分析与图像处理

除了上述应用外，矩阵对角化还可以用于聚类分析和图像处理等领域。在聚类分析中，我们可以利用矩阵对角化来提取数据的聚类结构并实现对数据的自动分类。在图像处理中，矩阵对角化可以用于图像压缩、去噪和特征提取等方面。