第1关：逻辑回归算法大体思想

#encoding=utf8
 
import numpy as np
 
#sigmoid函数
def sigmoid(t):
    #输入：负无穷到正无穷的实数
    #输出：转换后的概率值
    #********** Begin **********#
    result = 1.0 / (1 + np.exp(-t))
    #********** End **********#
    return round(result,12)
if __name__ == '__main__':
    pass

第2关：逻辑回归的损失函数 

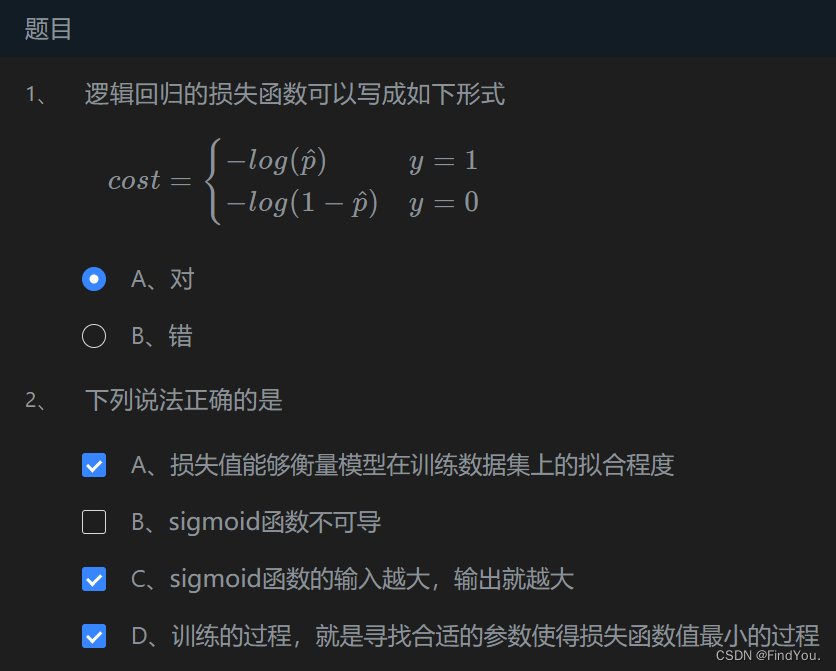
第3关：梯度下降

# -*- coding: utf-8 -*-
 
import numpy as np
import warnings
warnings.filterwarnings("ignore")
 
#梯度下降,inital_theta为参数初始值，eta为学习率，n_iters为训练轮数，epslion为误差范围
def gradient_descent(initial_theta,eta=0.05,n_iters=1e3,epslion=1e-8):
    #   请在此添加实现代码   #
    #********** Begin *********#
    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = 2*(theta-3)
        last_theta = theta
        theta = theta - eta*gradient
        if(abs(theta-last_theta)<epslion):
            break
        i_iter +=1
    #********** End **********#
    return theta

第4关：逻辑回归算法流程

# -*- coding: utf-8 -*-
 
import numpy as np
import warnings
warnings.filterwarnings("ignore")
#定义sigmoid函数
def sigmoid(x):
    return 1/(1+np.exp(-x))
 
#梯度下降，x为输入数据，y为数据label，eta为学习率，n_iters为训练轮数
def fit(x,y,eta=1e-3,n_iters=1e4):
    #   请在此添加实现代码   #
    #********** Begin *********#
    theta = np.zeros(x.shape[1])
    i_iter = 0
    while i_iter < n_iters:
        gradient = (sigmoid(x.dot(theta))-y).dot(x)
        theta = theta -eta*gradient
        i_iter += 1
    #********** End **********#
    return theta

 第5关：sklearn中的逻辑回归

#encoding=utf8
import warnings
warnings.filterwarnings("ignore")
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.model_selection import train_test_split
def cancer_predict(train_sample, train_label, test_sample):
    '''
    实现功能：1.训练模型 2.预测
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''
    
    #********* Begin *********#
    cancer = datasets.load_breast_cancer()
    #X表示特征，y表示标签
    X = cancer.data
    y = cancer.target
    ##划分训练集和测试集
 
    X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.20)
    logreg = LogisticRegression(solver='lbfgs',max_iter =200,C=10)
    logreg.fit(X_train, y_train)
    result = logreg.predict(test_sample)
    # print(result)
    return result
    #********* End *********#