【量算分析工具-水平距离】GeoServer改造Springboot番外系列四

news2024/9/25 13:18:55

水平距离

水平距离计算方式，我目前接触到的有四种：Flat Earth距离、大圆路径距离（Haversine公式）、JTS库方法（黑盒）、测地距离（Vincenty公式）。

说明：这里的EARTH_RADIUS使用的是椭球的平均半径6371008.77138m；有的地方使用椭球的长半径6,378,137m；个人觉得使用平均半径误差更小。

1、Flat Earth距离

地球上任意两点 A 和 B 的 Flat Earth 距离计算公式：

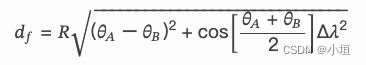
d_f：表示两个地点之间的平面距离 (flat distance)
R：表示地球的平均半径
θ_A、θ_B：表示两个地点的纬度 (latitude)，以弧度为单位
Δλ：表示两个地点的经度差 (longitude difference)，以弧度为单位

在这个公式下，假设地球是一个平面，而不考虑其真实的球形曲度。这种计算方法仅适用于近距离的近似计算，并不能准确地表示地球表面两点之间的实际距离。对于较大距离或需要高精度的距离计算，应使用更精确的距离计算方法。

需要注意的是，公式中的角度单位为弧度，而不是度数。所以在计算之前需要将纬度和经度的度数转换为弧度。

该方法的特点是计算速度快但精度不高，适用于纬度相差不大且对计算效率要求比较高的情况。

private static final double EARTH_RADIUS = 6371008.77138;  
 
   /**
     * 计算两点间的大圆距离，即直线距离（Flat Earth）
     *
     * @param lon1
     * @param lat1
     * @param lon2
     * @param lat2
     * @return double
     */
public static double getHorizontalDistance(double lon1, double lat1, double lon2, double lat2) {
        // 将经纬度转换为弧度
        double lat1Radians = Math.toRadians(lat1);
        double lon1Radians = Math.toRadians(lon1);
        double lat2Radians = Math.toRadians(lat2);
        double lon2Radians = Math.toRadians(lon2);

        // 计算两点之间的水平大圆距离
        double centralAngle = Math.acos(Math.sin(lat1Radians) * Math.sin(lat2Radians) +
                Math.cos(lat1Radians) * Math.cos(lat2Radians) * Math.cos(lon2Radians - lon1Radians));
        double horizontalDistance = EARTH_RADIUS * centralAngle;
        return horizontalDistance;
    }


    /**
     * 计算多点间的大圆距离，即折线长度
     *
     * @param coordinateList
     * @return double
     */
    public static double getHorizontalDistance(List<double[]> coordinateList) {
        if (coordinateList.size() < 2) {
            throw new IllegalArgumentException("The list must contain exactly two coordinates.");
        }
        double distance = 0;

        for (int i = 0; i < coordinateList.size() - 1; i++) {
            distance += getHorizontalDistance(coordinateList.get(i)[0], coordinateList.get(i)[1],
                    coordinateList.get(i + 1)[0], coordinateList.get(i + 1)[1]);
        }

        return distance;
    }

2、大圆路径距离（Haversine公式）

该方法将地球近似为一个半径为R的球，地球上任意两点 A 和 B 的大圆路径距离可以用 Haversine 公式计算：

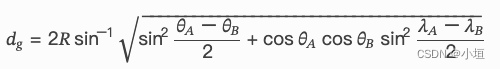
该方法是 GMT 默认使用的距离计算方法，适用于大多数情况。比如，-S5000f 表示距离为 5000 英尺。

有两个 GMT 参数可以控制大圆路径距离的计算细节，分别是：

PROJ_MEAN_RADIUS 地球平均半径
PROJ_AUX_LATITUDE 指定将大地纬度转换为多个适合球状近似的辅助纬度中的其中一个

需要注意，这两个选项仅当 PROJ_ELLIPSOID 不为 sphere 时才有效。

private static final double EARTH_RADIUS = 6371008.77138;


    /**
     * 计算两点间的大圆路径距离，即直线距离（Haversine公式）
     *
     * @param lon1
     * @param lat1
     * @param lon2
     * @param lat2
     * @return double
     */
    public static double getHorizontalDistance(double lon1, double lat1, double lon2, double lat2) {
        // 将经纬度转换为弧度
        double lat1Radians = Math.toRadians(lat1);
        double lon1Radians = Math.toRadians(lon1);
        double lat2Radians = Math.toRadians(lat2);
        double lon2Radians = Math.toRadians(lon2);
        double deltaLat = lat2Radians - lat1Radians;
        double deltaLon = lon2Radians - lon1Radians;
        // 计算两点之间的水平大圆距离
        double a = Math.sin(deltaLat / 2) * Math.sin(deltaLat / 2) +
                Math.cos(lat1Radians) * Math.cos(lat2Radians) *
                        Math.sin(deltaLon / 2) * Math.sin(deltaLon / 2);

        double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));

        double distance = EARTH_RADIUS * c;
        return distance;

    }
   /**
     * 计算多点间的大圆距离，即折线长度
     *
     * @param coordinateList
     * @return double
     */
    public static double getHorizontalDistance(List<double[]> coordinateList) {
        if (coordinateList.size() < 2) {
            throw new IllegalArgumentException("The list must contain exactly two coordinates.");
        }
        double distance = 0;

        for (int i = 0; i < coordinateList.size() - 1; i++) {
            distance += getHorizontalDistance(coordinateList.get(i)[0], coordinateList.get(i)[1],
                    coordinateList.get(i + 1)[0], coordinateList.get(i + 1)[1]);
        }

        return distance;
    }

3、JTS库方法

计算两点之间的距离

/**
     * 获取水平距离-JTS
     *
     * @param coordinateList
     * @return double
     */
    public static double getHorizontalDistanceJTS(List<double[]> coordinateList) throws FactoryException, TransformException {
        Coordinate[] coords = new Coordinate[coordinateList.size()];
        for (int i = 0; i < coordinateList.size(); i++) {
            coords[i] = new Coordinate(coordinateList.get(i)[0], coordinateList.get(i)[1]);
        }
        GeometryFactory geometryFactory = JTSFactoryFinder.getGeometryFactory();

        Point point0 = geometryFactory.createPoint(coords[0]);
        Point point1 = geometryFactory.createPoint(coords[1]);
        CoordinateReferenceSystem sourceCRS = CRS.decode("EPSG:4326");
        CoordinateReferenceSystem targetCrs = CRS.decode("EPSG:3857");
        boolean lenient = true;
        MathTransform transform = CRS.findMathTransform(sourceCRS, targetCrs, lenient);
        Geometry geometry0 = JTS.transform(point0, transform);
        Geometry geometry1 = JTS.transform(point1, transform);
        return geometry0.distance(geometry1);
    }



 public static void main(String[] args) throws FactoryException, TransformException {
        // 示例坐标和海拔高度，可以根据实际情况修改
        double lat1 = 28.70671; // 纬度1
        double lon1 = 115.877646; // 经度1

        double lat2 = 32.087038; // 纬度2
        double lon2 = 118.821214; // 经度2



        List<double[]> coordinateList = new ArrayList<>();
        coordinateList.add(new double[]{lon1, lat1});
        coordinateList.add(new double[]{lon2, lat2});

        getHorizontalDistanceJTS(coordinateList);
        
    }