1.建立DH坐标系

1.确定Zi轴（关节轴）

2.确定基础坐标系

3.确定Xi方向（垂直于zi和zi+1的平面）

4.完全确定各个坐标系 

例子：

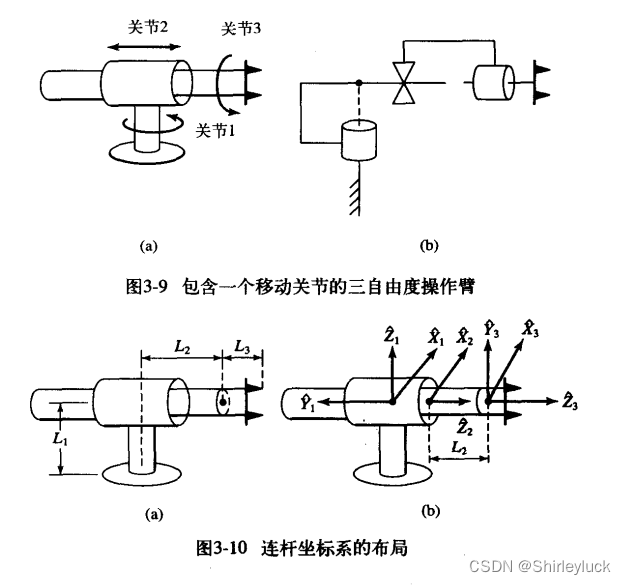
 坐标系的布局是由个人决定的，可以有不同的选择

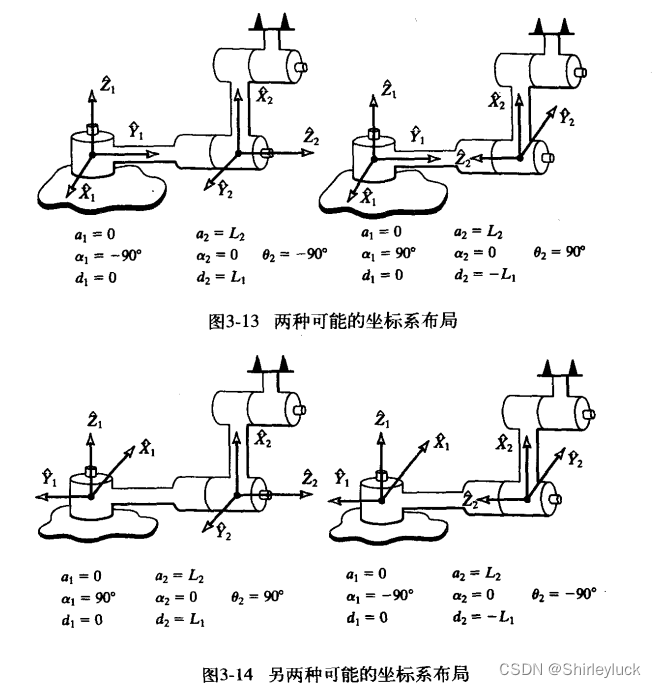
标准坐标系布局： 

 

2.DH参数表

个人理解
a z轴之间的距离，看下一个
α 转角 看下一个，看z绕本次的x轴旋转多少度到下一个z轴
d x轴之间距离，x看前一个
theta 转角
顺时针为负，逆时针为正

别人的详细解析：（写得好好！）

机器人正向运动学和D-H参数方法_d-h参数法-CSDN博客

3.MATLAB示例

 参考上图的DH参数表，将数据带入齐次变换矩阵中

clear;clc;
%%参数
L1=100;
L2=105;
L3=98;
L4=245;
IN_theta = [0,-45,10,10,0];

%DH
C_a=[0,0,L2,L3,0,0,0];
C_d=[0,L1,0,0,0,0,L4];
C_alpha=[0,-90,0,0,-90,0,0];
C_theta=[0,IN_theta(1),IN_theta(2),IN_theta(3),IN_theta(4)-90,IN_theta(5),0];

T_result = eye(4); % 初始化结果为单位矩阵

for i = 1:6
    T = [cosd(C_theta(i+1)) -sind(C_theta(i+1)) 0 C_a(i-1+1);
         sind(C_theta(i+1))*cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*cosd(C_theta(i+1)) -sind(C_alpha(i-1+1)) -sind(C_alpha(i-1+1))*C_d(i+1);
         sind(C_theta(i+1))*sind(C_alpha(i-1+1)) cosd(C_theta(i+1))*sind(C_alpha(i-1+1)) cosd(C_alpha(i-1+1)) cosd(C_alpha(i-1+1))*C_d(i+1);
         0 0 0 1]; % 根据给定的公式计算T[i]
    
    T_result = T_result * T; % 乘以每个T[i]
end