每日练习——同余方程以及格雷码

news2024/11/18 2:09:05

同余方程

题目描述

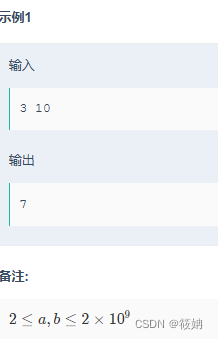
运行代码

#include<iostream>
#define ll long long
using namespace std;
ll exgcd(ll a, ll b, ll& x, ll& y) {
	if (!b)return x = 1, y = 0, a;
	ll d = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return d;
}
int main() {
		ll a, b, x, y;
		cin >> a >> b;
		ll d = exgcd(a, b, x, y);
		cout << (x + b) % b << endl;
	return 0;
}

代码思路

求解线性同余方程以及使用扩展欧几里得算法（Extended Euclidean Algorithm）求最大公约数（GCD）的功能。

扩展欧几里得算法（exgcd）

扩展欧几里得算法不仅仅计算两个整数a和b的最大公约数（GCD），还会找到一对整数x和y，满足以下等式：

ax + by = gcd(a, b)ax+by=gcd(a,b)

这里是算法的核心逻辑：

基本情况：如果b为0，说明a就是最大公约数，此时设置x=1,y=0，直接返回a。
递归调用：否则，递归调用exgcd(b, a % b, y, x)，这里交换了x和y的位置以便正确计算x和y的值。
更新x和y：根据递归调用返回的解，更新y的值为y - (a/b) * x，这里(a/b)是指整除，确保结果仍然是整数。
返回结果：最后返回计算得到的最大公约数d。

主函数（main）

输入：从用户那里接收两个整数a和b。
调用exgcd：使用exgcd(a, b, x, y)函数，求解a和b的最大公约数，并找到对应的x和y。
输出解的一部分：根据中国剩余定理或者其他相关应用场景，输出表达式(x + b) % b的结果。这里特别说明一下，这个输出并不直接对应于求解线性同余方程的标准形式解的展示，而是展示了一个特定操作的结果。通常，解决同余方程的目标是找到满足ax ≡ 1 (mod b)的x，即a关于b的乘法逆元，但这里的输出更像是一种示例操作，可能用于展示x的一个简单变形或特定场景的应用。

格雷码

题目描述

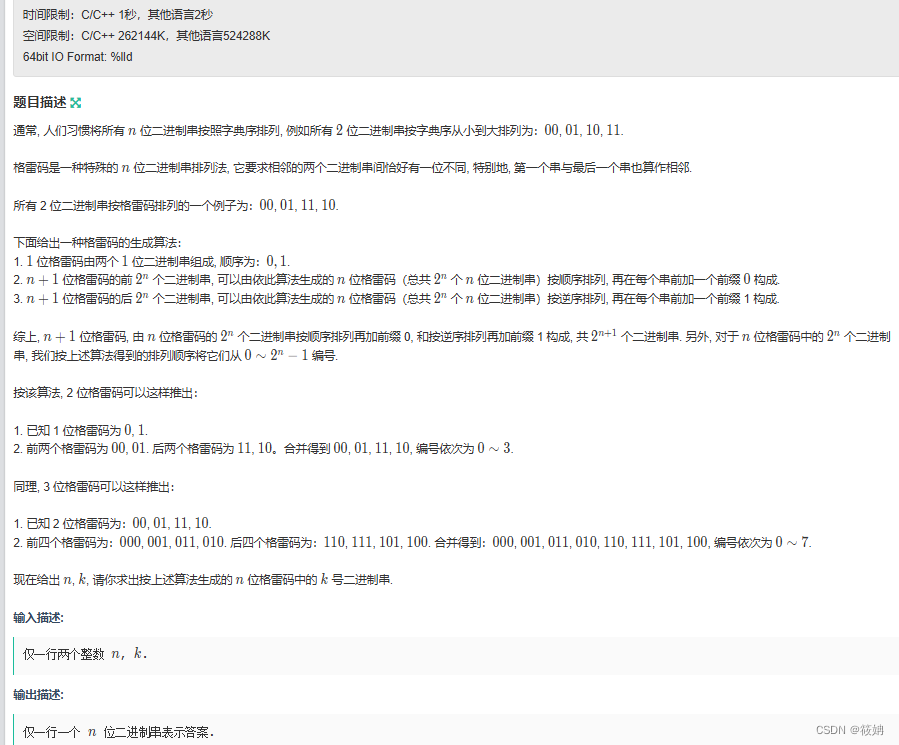
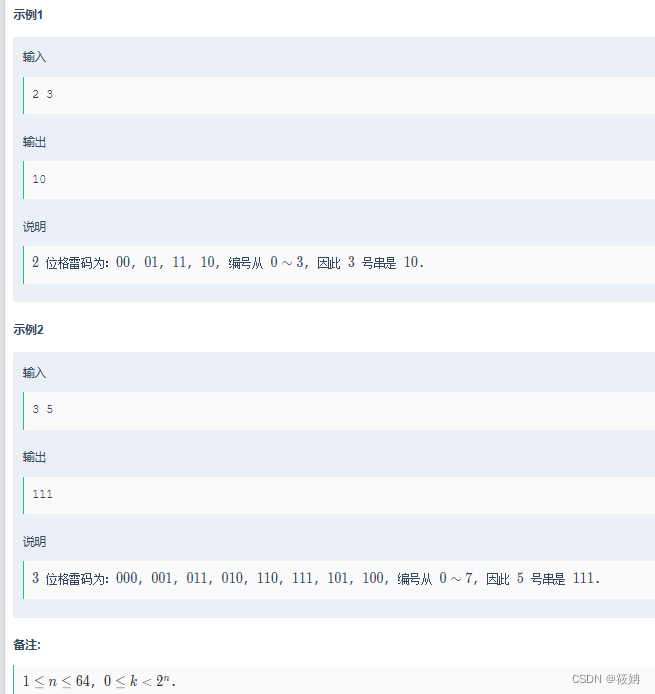
运行代码

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
#define ull unsigned long long
int main(){
    int n;
    ull a[65],k;
    string s;
    cin>>n>>k;
    a[0]=1;
    for(int i=1;i<=64;i++)
        a[i]=(a[i-1]<<1);
    for(int i=0;i<=64;i++)
        a[i]--;
    s.clear();
    while(n>=1){
        if(k>a[n-1])
            s+='1',k=a[n]-k;
        else s+='0';
        --n;
    }
    cout<<s<<endl;
}

代码思路

该程序首先计算每个二进制位上能表示的最大值（实际上是从1到2^n - 1的序列），然后根据输入的k值，决定在构造的二进制字符串中放置'1'还是'0'。下面是详细的代码思路分析：

初始化:
- 定义数组a用于存储从1个二进制位到64个二进制位所能表示的最大值。a[0]=1，之后每一项都是前一项左移一位再减1（即a[i] = (a[i-1] << 1) - 1），这是因为二进制位上能表示的最大数是从1开始的，如1位二进制最大是1（即2^1 - 1），2位是3（即2^2 - 1）等。
- 定义变量n存储位数，k存储要定位的值，s为最终输出的二进制字符串。
计算每个二进制位的最大值:
- 使用循环计算并存储每个二进制位的最大值到数组a中。这一步是为后续比较做准备。
构建二进制字符串:
- 进行循环，每次循环检查当前位（从最高位到最低位）是否足够放置k。如果k大于或等于当前位的最大值（即a[n-1]），说明当前位应该是1（因为k在这个范围内），并且从k中减去当前位能表示的值（a[n] - k），然后将s的当前位设置为'1'。否则，如果k小于当前位的最大值，则在s中放置'0'。
- 每次处理完一个位，就减少n的值，表示考虑下一个更低的二进制位。
输出结果:当所有的位都被处理过后，输出构建好的二进制字符串s。