【数据结构】栈和队列超详细解析

最重要的就是不要去看远方模糊的，而要做手边清楚的事。💓💓💓

✨说在前面

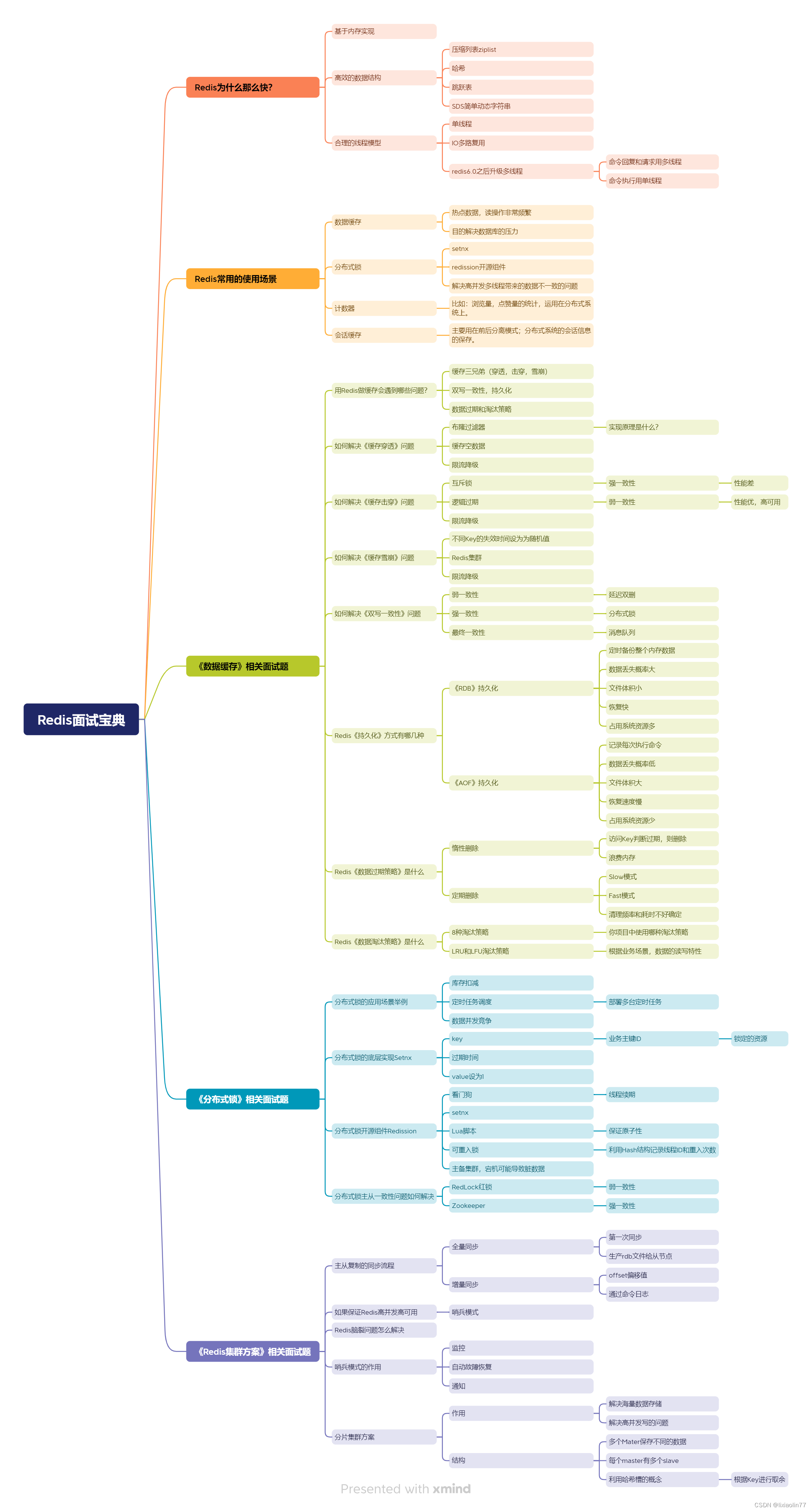
🍋知识点一：栈

• 🌰1.什么是栈？

• 🌰2.如何实现栈

• 🌰3.栈的基本操作

🔥栈的初始化

🔥判断扩容与申请空间

🔥入栈操作（压栈）

🔥出栈操作（弹栈

🔥获取栈顶数据

🔥检测栈是否为空

🔥获取栈中有效元素个数

🔥栈的销毁

🍋知识点二：队列

• 🌰1.什么是队列？

• 🌰2.如何实现队列？

• 🌰3.队列的基本操作

🔥队列的初始化

🔥队尾入队列

🔥队头出队列

🔥获取队列中有效元素个数

🔥获取队列头部元素

🔥获取队列尾部元素

🔥检测队列是否为空

🔥销毁队列

• ✨SumUp结语

✨说在前面

亲爱的读者们大家好！💖💖💖，我们又见面了，在之前的阶段我们学习了顺序表、链表，包括单链表和双向链表，还刷了一些算法OJ练习。这些题目很多都是非常经典的，希望大家可以认真对待，仔细分析，提升自身的算法能力。

今天我们将要学习两种新的数据结构-栈和队列，那什么是栈，什么是队列，他们用什么来实现，又有什么作用呢？我们今天就解开它神秘的面纱，详细剖析这两种新的数据结构吧~

👇👇👇
💘💘💘知识连线时刻（直接点击即可）

🎉🎉🎉复习回顾🎉🎉🎉

LeetCode/NowCoder-链表经典算法OJ练习3

LeetCode/NowCoder-链表经典算法OJ练习4

博主主页传送门：愿天垂怜的博客

🍋知识点一：栈

• 🌰1.什么是栈？

不同于直接将晦涩的概念扔给你，这样容易让身为初学者的你难以理解，我们先来看一下生活中的一些例子：

这时我们再生活中很常见的——羽毛球筒。这个羽毛球筒有什么特点呢？它的一端是封住的，我们在放入或者拿出羽毛球的时候需要再另一端操作。而且，最先放进去的总是最后拿出来的，而最后放进去的总是最先拿出来的。

那如果我们把羽毛球筒抽象成是一种数据结构，那么羽毛球就是数据，这种数据结构满足一端是封住的，我们要添加或者删除数据都只能在另一端操作，而且满足最先加入的数据总是最后拿出，最后添加的数据总是最先拿出，那么这种数据结构就是栈。

现在来说，相信你已经大概了解什么是栈了，现在再给出具体概念，相信是可以增进你的理解的。

栈（Stack）是一种特殊的线性数据结构，它的特殊之处在于其操作顺序是后进先出（Last In First Out，LIFO）的，即最后压入栈的元素最先弹出。

进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈，出数据也在栈顶。

• 🌰2.如何实现栈

那我们可以使用什么工具实现栈呢？我们之前学过了顺序表（数组）、单链表、双向链表，那用哪种实现栈最合适呢？

首先三种方式都可以实现，特别注意如果使用单链表，应该将头部当做是栈顶，这样进行压栈和弹栈就相当于是头插和头删，比较方便。但是如果将单链表的尾部当做是栈顶，尾删是需要找到最后一个节点的，而对于单链表不好找最后一个节点，它需要循环遍历，如果一定要将尾部当做栈顶，就要用双向链表。

在三种方式都可以实现的情况下，我们首先排除双向链表。因为既然单链表就可以了，就没必要用双向链表，毕竟双向链表所需要维护的指针更多，那么所需要的空间就会更大。

但是对比数组，单链表的数据在内存中不是连续的，这会造成单链表的缓存利用率和命中率更低，所以用数组，而且用动态顺序表来实现是比较合适的。

栈的结构如下：

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;//数组
	int top;//栈顶的下一个位置
	int capacity;//容量
}ST;

在顺序表中，我们的size指的是数组中的有效元素个数，但其实如果将size作为数组下标的话，其实a[size]指的是最后一个数据的下一个位置的数据。在实现栈的时候，我们将size改为top，显然，top的位置应该是栈顶的下一个位置。比如，现在数组有三个元素，分别为20、30、40，那么top应该为3，而下标为3的位置应该在40的后面，因为40这个数据的下标为2。所以，这个地方的top不仅表示有效数据个数，同时也是栈顶下一个位置的下标。

• 🌰3.栈的基本操作

🔥栈的初始化

初始化栈其实就是初始化数组、数组元素个数和容量。刚开始没有任何数据，所以pst->a我们置为NULL，而刚开始的数组元素个数和容量都为0。

void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	//top指的是栈顶数据的下一个位置
	pst->top = pst->capacity = 0;
}

这里也能发现，其实当栈中没有数据的时候，我们的top就是0，下标为0的位置其实就是第一个位置，如果栈中有一个数据，那么它就是1，是第二个位置...总之，top是栈顶数据的下一个位置。

🔥判断扩容与申请空间

在对栈进行压栈或弹栈，都需要检查空间是否足够，如果不够，我们需要及时扩容，一般扩大到原来的两倍即可，特殊地，如果原来的空间为0，那么就创建四个字节的空间。

static void STCheckCapacity(ST* pst)
{
	if (pst->top == pst->capacity)//如果有效个数和总容量相等
	{
		int NewCapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
		STDataType* temp = (STDataType*)realloc(pst->a, NewCapacity * sizeof(STDataType));
		if (temp == NULL)
		{
			perror("realloc operation failed");
			exit(1);
		}
		pst->a = temp;
		pst->capacity = NewCapacity;
	}
}

可以发现，不论是栈的初始化，还是扩容操作，其实和动态顺序表都是一样的。

🔥入栈操作（压栈）

相当于在将top位置数据设置为x，再将top++，比较简单。在操作前，首先检查是否需要扩容。

void STPush(ST* pst, STDataType x)
{
	assert(pst);
	STCheckCapacity(pst);
	pst->a[pst->top++] = x;
}

🔥出栈操作（弹栈）

类似于动态顺序表，只要让top--就好了，如法炮制，非常简单。不过top既然要--，那就必须保证top是大于0的，所以在assert断言一下就好了。

void STPop(ST* pst)
{
	assert(pst && pst->top);
	pst->top--;
}

🔥获取栈顶数据

同样的道理，返回数组中最后一个有效数据，注意位置是top-1而不是top，同时保证top是大于0的。

STDataType STTop(ST* pst)
{
	assert(pst && pst->top);
	return pst->a[pst->top - 1];
}

🔥检测栈是否为空

当栈为空时，数组没有数据，此时top的值为0，所以我们检查top的值是否为0就可以了，我们可以同布尔类型的函数。

bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}

🔥获取栈中有效元素个数

栈中有效元素的个数就是top的值，直接返回top即可。

int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

🔥栈的销毁

销毁栈就是释放先前动态申请的pst->a，同时置为NULL，再将top和capacity的值置为0，和顺序表如出一辙。

void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}

🍋知识点二：队列

• 🌰1.什么是队列？

同样我们先来理解生活中的例子：

我们再结账、医院挂号、旅游时购物经常需要排队，从而形成一个队列。在这个队列中，最先排队进去的人最先出来，而最后排队的是最后出来的。

现在我们将排队抽象成一种数据结构——队列，那么数据就是排队的人，队列中的数据满足先插入的数据先出，后插入的数据后出。

现在，给出队列的概念：

队列（Queue）是一种常用的数据结构，其特点是遵循“先进先出”（First In First Out，FIFO）的原则，即最先进入队列的元素最先被取出。类比现实生活中排队的场景，先到先得，后到只能等待。

队列只允许在一端进行插入数据操作，在另一端进行删除数据操作，进行插入操作的一端称为队尾，进行删除操作的一端称为队头。

• 🌰2.如何实现队列？

同样，我们思考用什么工具实现队列？是用顺序表（数组）、单链表还是双向链表？

还是同理，在三者都可以实现队列的情况下，我们不考虑双向链表，因为需要维护更多的指针，就需要创建更多的空间。

那用数组还是链表呢？

显然数组是做不好这个事情的。我们需要再队头插入数据，还需要在队尾删除数据，并且对数组来说这样的操作如果可行，也需要移动数组中的所有其他元素来填补被删除元素的位置，这是一个O(n)的操作，而在链表中，入队和出队操作都可以在O(1)的时间内完成，因为只需要调整几个指针。

所以，用单链表来实现队列是比较合适的。

队列的结构如下：

typedef int QDataType;

typedef struct QueueNode//队列中的节点元素
{
	QDataType val;//数据
	struct QueueNode* next;指向下一个队列节点的指针
}QNode;

typedef struct Queue//包含指向头尾节点的指针
{
	struct QueueNode* phead;//指向头节点的指针
	struct QueueNode* ptail;//指向尾节点的指针
	int size;//队列中有效元素的个数
}Queue;

注意，在单链表的实现中，我们频繁地会用到指向头节点的指针和指向尾节点的指针（循环遍历），那这样实现队列，每次传参可能比较麻烦，而且还要传二级指针。所以我们在实现队列的时候，不妨设置一个结构体Queue用来保存这两个指针，这样不仅传参少了，而且不用传二级指针。同时，也可以将节点个数也放在这个结构体中，方便后续操作。

• 🌰3.队列的基本操作

🔥队列的初始化

初始化队列就是将Queue类型结构体的变量中，指向头尾节点的指针都只为NULL，同时队列中是没有数据的，size为0。

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

🔥队尾入队列

我们只有在队尾入队列的时候才会创建节点，所以我们不单独封装一个申请节点的函数，直接在这个函数内部就可以了。同时如果你像我一样没有创建哨兵位的话，需要单独讨论入队列的时候队列是否为空。

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
    //动态申请节点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc operation failed");
		exit(1);
	}
	newnode->next = NULL;
	newnode->val = x;
    //如果队列中没有节点
	if (pq->ptail == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
    //如果队列中有节点
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

🔥队头出队列

出队列也需要分情况讨论，第一种情况是只有一个节点，此时我们直接释放这个节点再把指向头尾两个节点的指针全部置为NULL就可以了。第二种情况是节点数大于1，此时我们需要创建next指针用来保存pq->phead的下一个节点，不然free释放后就找不到这个节点了。同时由于size需要--，所以需要保证size大于0。

void QueuePop(Queue* pq)
{
	assert(pq && pq->size);
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

🔥获取队列中有效元素个数

剩下部分的代码就比较简单了，简单操作就可以搞定，大家也可以自己试试能不能写出，再来和我写的进行对照。

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

🔥获取队列头部元素

由于需要访问头节点的值，所以assert中需要添加phead指针，以确保可以访问。

QDataType QueueFront(Queue* pq)
{
	assert(pq && pq->phead);
	return pq->phead->val;
}

🔥获取队列尾部元素

由于需要访问尾节点的值，所以assert中需要添加ptail指针，以确保可以访问。

QDataType QueueBack(Queue* pq)
{
	assert(pq && pq->ptail);
	return pq->ptail->val;
}

🔥检测队列是否为空

size就代表了队列中数据的个数，所以直接判断size是否为0即可，我们可以用布尔类型。

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

🔥销毁队列

销毁队列需要像单链表那样，用next指针保存下一个节点的值，然后循环遍历这个队列，最后将两个指针置NULL，size置0。

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

• ✨SumUp结语

到这里本篇文章的内容就结束了，其实栈和队列都是用我们之前已经学过的数据结构来实现的，如栈的实现基本就和动态顺序表一样，队列的实现基本就和单链表一样，如果大家对之前的数据结构不熟悉，也可以点击我的主页进行学习。OK，既然都看到这里了，如果大家觉得有帮助，麻烦大家点点赞，如果有错误的地方也欢迎大家指出~