数据结构——链式二叉树知识点以及链式二叉树数据操作函数详解！！

引言：该博客将会详细的讲解二叉树的三种遍历方法：前序、中序、后序，也同时会讲到关于二叉树的数据操作函数。值得一提的是，这些函数几乎都是建立在一个函数思想——递归之上的。这次的代码其实写起来十分简单，用不了几行就可以解决问题，但是其中的代码思想和运作方式才是难点。但只要我们搞懂了思想，手撕代码完全就没问题了，就让我们一起加油吧！

更多有关C语言和数据结构知识详解可前往个人主页：计信猫

一，二叉树的遍历方式

0，三序前言

1，前序

2，中序

3，后序

二，二叉树的数据操作函数

1，二叉树节点个数

2，二叉树叶子节点个数

3，二叉树高度

4，二叉树第k层节点个数

5，查找值为x的节点

6，二叉树的销毁

三，二叉树的层序遍历

1, 层序遍历

2，判断完全二叉树

四，结语

一，二叉树的遍历方式

0，三序前言

其实我们所说的三序其实就可以分为前序、中序、后序，它们分别表示对一棵二叉树不同的遍历方式。我们在这里先对它们的遍历方式做一次总结：

●前序：根，左子树，右子树

●中序：左子树，根，右子树

●后序：左子树，右子树，根

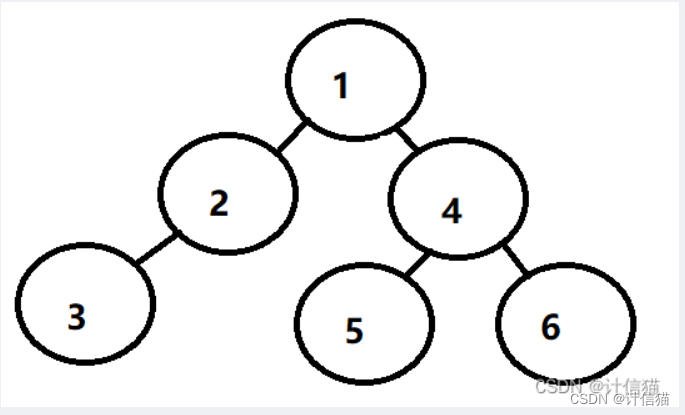
在这里，我们以如下的二叉树为例子进行三序的介绍：

于是我们使用如下的代码在VS中直接手搓出上图的二叉树，以方便我们后续对代码的检测。

typedef int BTDataType;
//二叉树节点
typedef struct BinaryTreeNode
{
	BTDataType val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;
//创建节点
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	newnode->val = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
//创建二叉树
BTNode* CreatBinaryTree()
{
	//创建节点
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	//将节点按照图示连起来
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	//node1为根节点
	return node1;
}

并且，我们仍然使用三文件操作法，如下图所示：

1，前序

●前序：根，左子树，右子树

那么对于该二叉树，我们应该如何遍历呢？

按照前序遍历的要求，我们就可以将一棵二叉树不断地划分为根、左子树、右子树。

只有在我们将node1的左子树遍历完之后我们才可以进入右子树。而node1的左子树又可以被视作以node2为根，并且包含左右子树的一棵新树，所以我们又需要对新的树进行前序遍历。如此循环下去，其实递归的思想也就慢慢体现出来了。

所以，以上的树被遍历完之后的结果如下所示，其中N表示NULL空节点：

所以前序遍历的代码如下：

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}

2，中序

●中序：左子树，根，右子树

现在，我们以中序遍历法遍历如下二叉树：

所以，我们还是将这棵二叉树不断地分解为根，左子树，右子树三个部分。但是我们这一次就会改变顺序，我们需要先遍历完左子树后再进行根的遍历，最后才进行右子树的遍历。而以node1为根节点的左子树又可以继续被细分为以上三个部分，所以我们又需要进行中序遍历，直到某个节点的左子树被遍历完（为空），方可进行根的遍历。

所以，以上的树被中序遍历完之后的结果如下：

所以中序遍历的代码入下：

//中序遍历
void MidOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	MidOrder(root->left);
	printf("%d ", root->val);
	MidOrder(root->right);
}

3，后序

●后序：左子树，右子树，根

如果我们使用后序遍历法遍历如下二叉树，又会是怎样一个结果呢？

所以我们仍然以之前学到的方式进行递归类推，先遍历完node1的左子树，后遍历node1的右子树，最后在遍历根node1。而在遍历node1的子树时，它的子树又可以被视为以node2或node4为根节点的新树，故我们又对其再进行后序遍历，直到遇到空节点。

所以我们模拟遍历之后的结果如下图所示：

那么，后序遍历的代码入下：

//后序遍历
void BackOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	BackOrder(root->left);
	BackOrder(root->right);
	printf("%d ", root->val);
}

二，链式二叉树的数据操作函数

1，二叉树节点个数

当我们想要知道一棵二叉树中有多少个节点的时候，我们就可以使用这个函数。

//求二叉树中的节点个数
int TreeSize(BTNode* root);

在这个函数中，我们还是使用到了递归的思想。我们可以将一棵树的总节点个数分为一个根节点与它的左右两子树的节点和。然后它的子树又可以再次使用这个方法将它的子树拆分，直到遇到NULL就递归结束，返回值为0。所以我们的代码如下：

//求二叉树中的节点个数
int TreeSize(BTNode* root)
{
	//遇到空，递归结束开始返回
	if (root == NULL)
	{
		return 0;
	}
	//将二叉树拆分为根和左右两子树之和
	return TreeSize(root->right) + TreeSize(root->left) + 1;
}

2，二叉树叶子节点个数

这个函数用于求的一棵二叉树之中的叶子节点的个数。

//求二叉树中叶子节点的个数
int TreeLeafSize(BTNode* root)

首先，我们可以确定的是，当一个节点的左右两子节点全为NULL时，那么这个节点就是叶节点。而当我们想要找到一棵二叉树中的叶节点个数时，我们就可以将总的叶节点的个数拆分为左右两子树的叶节点之和。然后我们不停以以上方式进行拆分，直到找到叶节点就递归结束，返回值为1。而要注意，空树的叶节点个数为0，要特殊讨论。所以按照以上的思想进行代码实现如下：

//求二叉树中叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	//空树没有叶节点
	if (root == NULL)
	{
		return 0;
	}
	//找到了叶节点，递归结束，返回1
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//开始递归
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3，二叉树高度

二叉树的高度其实就是二叉树的度，也就是它的最大高度。

//求二叉树的高度
int TreeHeight(BTNode* root);

当我们想要找到一棵树的最大高度的时候，其实我们就可以将这棵树的高度拆分为左子树与右子树中高度的较大值加上1（其中1代表了根也占一层高度）。如此递归下去，当我们递归到叶节点时，就递归结束，返回值为1。当然最后我们也需要注意，空树的高度为0。所以我们的代码如下：

//求二叉树的高度
int TreeHeight(BTNode* root)
{
	//空树高度为0
	if (root == NULL)
	{
		return 0;
	}
	int left = TreeHeight(root->left);
	int right = TreeHeight(root->right);
	return left > right ? left + 1 : right + 1;
}

4，二叉树第k层节点个数

该函数则专门用于求出一棵二叉树中第k层的节点个数。

//求二叉树第k层的节点个数
int TreeLevelKSize(BTNode* root, int k)；

对于这个函数的实现，还是请出我们的老朋友——递归。对于一棵二叉树，求它第k层的节点个数时，我们就可以将这个问题视为求其根节点的左右子树的（k-1）层的节点个数之和。直到k持续减一，使k==1时，说明该层就是我们的第k层，此时递归结束，返回值为1就可以了。所以我们的代码如下：

//求二叉树第k层的节点个数
int TreeLevelKSize(BTNode* root, int k)
{
	//空树则返回0
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	//根节点的左右子树的（k-1）层的节点个数之和
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

5，查找值为x的节点

此函数用于查找二叉树中值为x的节点，并返回该节点的地址。

//查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x);

既然我们想要找到值为x的节点时，那遍历这个二叉树就必不可少了！所以我们就可以使用之前学到的三序遍历之一的前序遍历法。我们先遍历根，若根节点不是x节点我们就对它的左子树进行遍历，最后再对右子树遍历。若二叉树为空或者不存在x节点我们都返回NULL。所以我们的代码方法如下：

//查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	//为空树就返回NULL
	if (root == NULL)
	{
		return NULL;
	}
	//先遍历根节点
	if (root->val == x)
	{
		return root;
	}
	//再遍历左子树
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)//ret1不为空，说明x存在于左子树
	{
		return  ret1;
	}
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)//ret2不为空，说明x存在于右子树
	{
		return ret2;
	}
	//整棵二叉树都不存在x节点，返回NULL
	return NULL;
}

6，二叉树的销毁

当我们要结束对二叉树的操作时，我们就需要对二叉树进行销毁操作，防止内存泄漏。

//二叉树的销毁
void TreeDestroy(BTNode* root);

在我们对二叉树进行遍历销毁时，我们就应该选择后序遍历，将根节点进行最后销毁，因为一旦将根节点先行销毁之后，那么我们就找不到根节点所对应的左右子树了，就无法进行后续销毁了。所以代码如下：

//二叉树的销毁
void TreeDestroy(BTNode* root)
{
	if (root == NULL)
		//遇到空说明遍历结束，开始返回
	{
		return;
	}
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

三，链式二叉树的层序遍历

1, 层序遍历

二叉树的层序遍历属于广度优先遍历（BFS），而二叉树的层序遍历其实就是对二叉树进行一层一层的遍历，完成二叉树的层序遍历需要用到我们之前学到的队列的知识。

现在我们对队列进行一定的改装。以前我们所学到的队列中储存的为int类型的值，而这时候我们将int改变为二叉树节点的指针。经过以上操作之后，那么这个队列里所储存的就是二叉树节点的指针了。

typedef struct BinaryTreeNode* QDataType;
//二叉树的层序遍历
void TreeLevelOrder(BTNode* root);

我们现在以以下的二叉树为例子：

我们首先在队列中插入根节点：

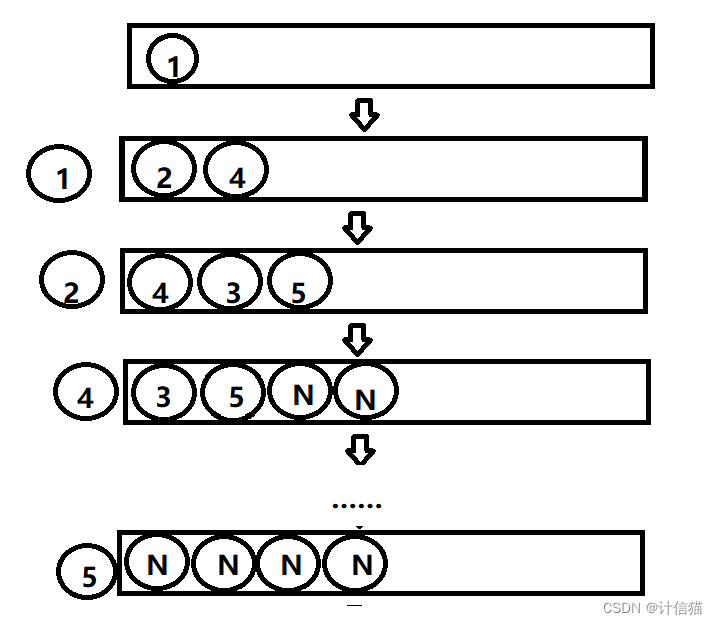
然后我们取出根节点，并且同时在队列中加入其子节点2和4：

后我们取出节点2并且再次于队列中加入节点2对应的子节点（空则不进入队列）。

以此类推，直到当我们取出的节点为空时，那么此时对于这个二叉树的层序遍历就结束了。而在遍历的过程中，我们始终遵循一个思想，就是上层带下层。所以在此思想的基础之上，我们便可以写出层序遍历的代码：

//二叉树的层序遍历
void TreeLevelOrder(BTNode* root)
{
	assert(root);
	//创建一个队列
	Queue q;
	//初始化队列
	QueueInit(&q);
	//向队列中插入第一个元素
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取出队首节点并且打印
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->val);
		//加入队首节点的非空子节点
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
}

2，判断完全二叉树

当我们需要判断一棵树是否为完全二叉树时我们就可以使用该函数，它的返回值为布尔类型。

//完全二叉树的判断
bool TreeComplete(BTNode* root);

在写该函数时，我们则会用到以下的思路：

1，层序遍历这个二叉树，并且空指针也进入队列

2，取出队首节点遇到第一个空节点时，就开始进行判断，如果队列里面节点全为空就为完全二叉树，后面有非空节点就不为完全二叉树

让我们结合下列的例子进行理解：

我们以之前我们学到的层序遍历法来遍历这个二叉树，如下图所示：

现在就是我们取出第一个空节点的时候，此时我们就对队列里的元素进行判断，如果队列里边全为空指针，那么这个二叉树就为完全二叉树，否则就不为完全二叉树。而由我们的例子可见，该二叉树就为完全二叉树。

所以我们就可以将此方法转变为如下的代码：

//完全二叉树的判断
bool TreeComplete(BTNode* root)
{
	assert(root);
	//创建一个队列
	Queue q;
	//初始化队列
	QueueInit(&q);
	//向队列中插入第一个元素
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取出队首节点
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//若取出的节点为空，就跳出循环，并对队列中的节点进行判空
		if (front == NULL)
		{
			break;
		}
		//不管是否为空，节点的子节点都加入队列
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	//判断队列中的节点
	while (!QueueEmpty(&q))
	{
		//取出队首节点
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//队列中有节点不为空，则不为完全二叉树
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}