一、等价关系的定义
设R是集合A上的一个二元关系,如果R满足自反性、对称性和传递性,则称R是一个等价关系。

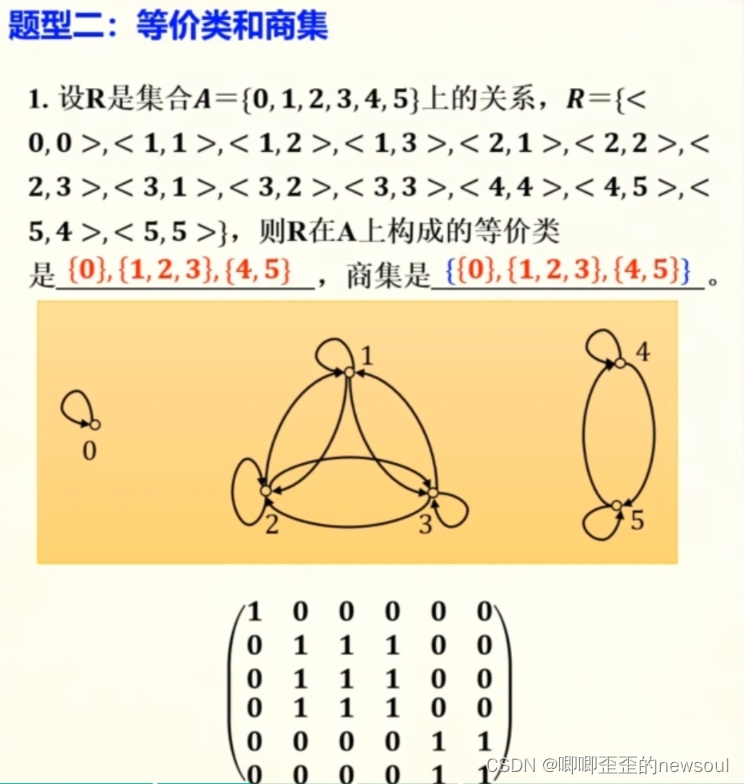
二、等价类和商集
哪些元素有关系,就构成一个等价类。
所有等价类构成的集合就是商集。
集合的划分:就是对集合中的元素分组,每个元素在且仅在某一组。
三、偏序关系的定义
设R是集合A上的一个二元关系,如果R满足自反性、反对称性和传递性,则称R是一个等价关系。
典型的偏序关系:
1·大于等于/小于等于关系
2·正整数或其任何子集上的整除关系
3·任何集合的幂集上的包含关系

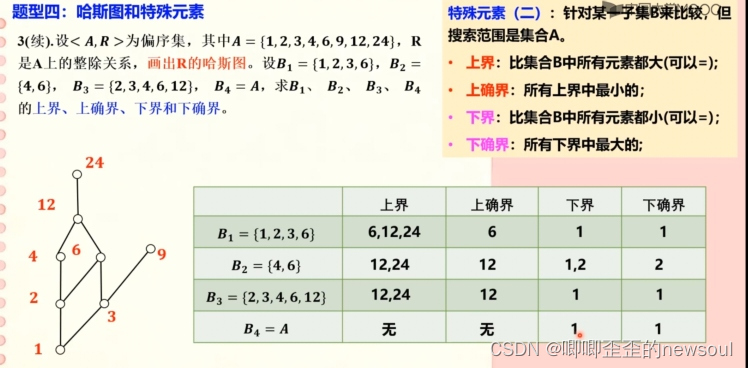
四、哈斯图和特殊元素
关系图变哈斯图的步骤:1·去掉所有环2·去掉可由传递性得到的边3·移动结点位置,令所有箭头方向向上,然后省掉箭头
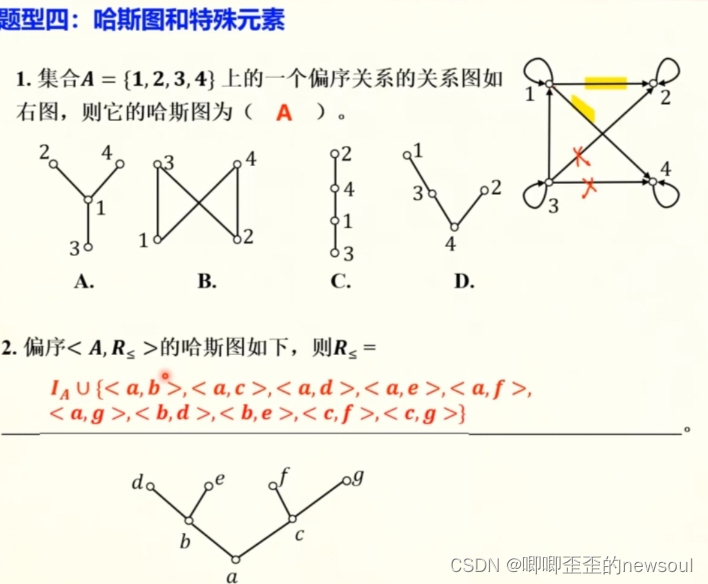
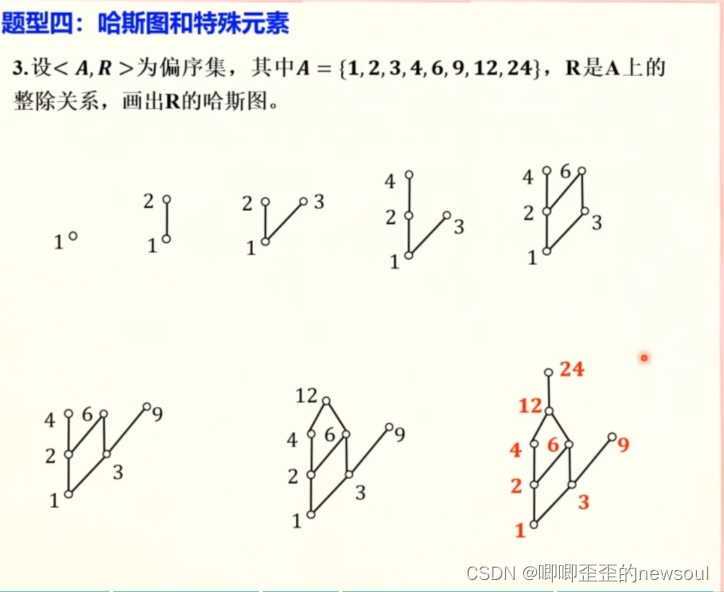
整除关系画哈斯图的简便方法:
1·先画最小数值的结点,然后从小到大依次决定每个元素的位置
2·决定的方法:找到所有能整除它的元素中的高点(可能有多个),置于其上方并连线。如果找不到,奇就只在旁边画一个结点。
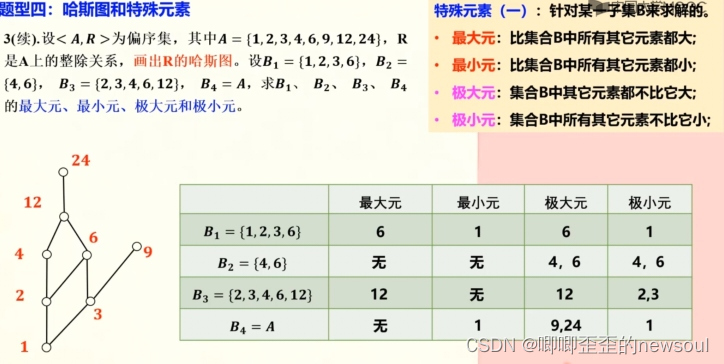
特殊元素:
最大元:比集合B中所有其他元素都大;
最小元:比集合B中所有其他元素都小;
极大元:集合B中其他元素都不比它大;
极小元:集合B中所有其他元素不比它小。
上界与下界: