一、查漏补缺复盘

1、python中zip()用法

python中zip()用法

应用举例

import numpy as np
import matplotlib.pyplot as plt
 
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
 
def forward(x):
    return x*w
 
 
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2
 
 
# 穷举法
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
    print("w=", w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val, y_val)
        l_sum += loss_val
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum/3)
    w_list.append(w)
    mse_list.append(l_sum/3)
    
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()    

2、Tensor和tensor的区别

首先看下代码区别

>>> a=torch.Tensor([1,2])
>>> a
tensor([1., 2.])
>>> a=torch.tensor([1,2])
>>> a
tensor([1, 2])

• torch.Tensor()是python类，更明确地说，是默认张量类型torch.FloatTensor()的别名，torch.Tensor([1,2])会调用Tensor类的构造函数__init__，生成单精度浮点类型的张量。
• 而torch.tensor()仅仅是python函数：https://pytorch.org/docs/stable/torch.html torch.tensor

torch.tensor(data, dtype=None, device=None, requires_grad=False)

• 其中data可以是：list, tuple, NumPy ndarray, scalar和其他类型。
  torch.tensor会从data中的数据部分做拷贝（而不是直接引用），根据原始数据类型生成相应的torch.LongTensor、torch.FloatTensor和torch.DoubleTensor。

3、计算图中的迭代取数

注意关注grad取元素规则

import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
w = torch.tensor([1.0]) # w的初值为1.0
w.requires_grad = True # 需要计算梯度
 
def forward(x):
    return x*w  # w是一个Tensor
 
 
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2
 
print("predict (before training)", 4, forward(4).item())
 
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l =loss(x,y) # l是一个张量，tensor主要是在建立计算图 forward, compute the loss
        l.backward() #  backward,compute grad for Tensor whose requires_grad set to True
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data   # 权重更新时，注意grad也是一个tensor
 
        w.grad.data.zero_() # after update, remember set the grad to zero
 
    print('progress:', epoch, l.item()) # 取出loss使用l.item，不要直接使用l（l是tensor会构建计算图）
 
print("predict (after training)", 4, forward(4).item())

.data等于进tensor修改，.item()等于把数拿出来

• w是Tensor(张量类型)，Tensor中包含data和grad，data和grad也是Tensor。grad初始为None，调用l.backward()方法后w.grad为Tensor，故更新w.data时需使用w.grad.data。如果w需要计算梯度，那构建的计算图中，跟w相关的tensor都默认需要计算梯度。
  

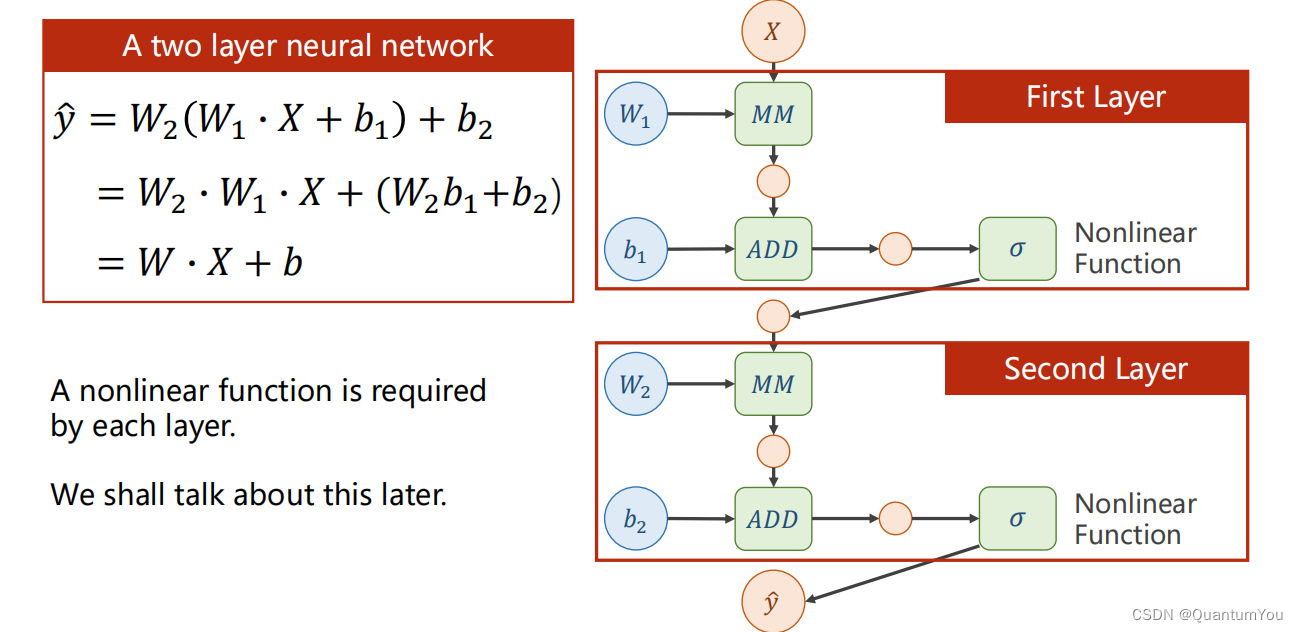
下面的 Linear(1,1 )是input1，output1

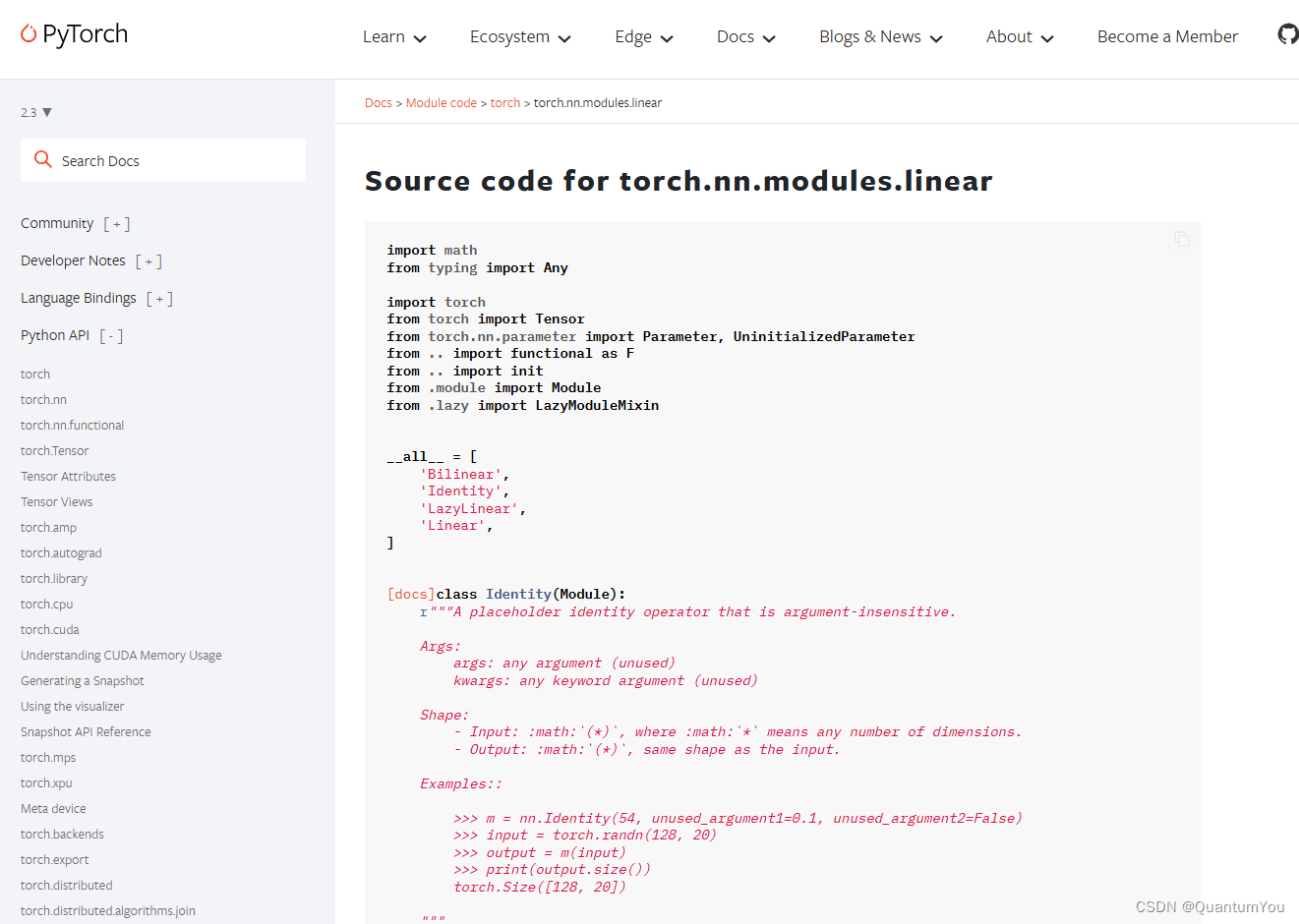
4、nn.Modlue及nn.Linear 源码理解

import torch
# prepare dataset
# x,y是矩阵，3行1列 也就是说总共有3个数据，每个数据只有1个特征
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
 
 
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        # (1,1)是指输入x和输出y的特征维度，这里数据集中的x和y的特征都是1维的
        # 该线性层需要学习的参数是w和b  获取w/b的方式分别是~linear.weight/linear.bias
        self.linear = torch.nn.Linear(1, 1)
 
    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred
 
model = LinearModel()
 
# construct loss and optimizer
# criterion = torch.nn.MSELoss(size_average = False)
criterion = torch.nn.MSELoss(reduction = 'sum')
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01) # model.parameters()自动完成参数的初始化操作，这个地方我可能理解错了
 
# training cycle forward, backward, update
for epoch in range(100):
    y_pred = model(x_data) # forward:predict
    loss = criterion(y_pred, y_data) # forward: loss
    print(epoch, loss.item())
 
    optimizer.zero_grad() # the grad computer by .backward() will be accumulated. so before backward, remember set the grad to zero
    loss.backward() # backward: autograd，自动计算梯度
    optimizer.step() # update 参数，即更新w和b的值
 
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
 
x_test = torch.tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

参考文章

import torch
from torch import nn

m = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)

output.size()   # torch.Size([128, 30])

• nn.Module 是所有神经网络单元（neural network modules）的基类
  pytorch在nn.Module中，实现了__call__方法，而在__call__方法中调用了forward函数。
• 首先创建类对象m，然后通过m(input)实际上调用__call__(input)，然后__call__(input)调用
  forward()函数，最后返回计算结果为：[ 128 , 20 ] × [ 20 , 30 ] = [ 128 , 30 ]

链接

5、知识杂项思考列表

1、SGD单个样本进行梯度下降容易被噪声带来巨大干扰

2、矩阵求导理论书籍 matrix cookbook

3、前向传播是为了计算损失值，反向传播是为了计算梯度来更新模型的参数

6、KL散度初步理解

• KL散度（Kullback-Leibler divergence）是两个概率分布间差异的非对称性度量。参与计算的一个概率分布为真实分布，另一个为理论（拟合）分布，相对熵表示使用理论分布拟合真实分布时产生的信息损耗。

KL散度具有以下几个性质：

1. 非负性：KL散度的值始终大于等于0，当且仅当两个概率分布完全相同时，KL散度的值才为0。
2. 不对称性：KL散度具有方向性，即P到Q的KL散度与Q到P的KL散度不相等。
3. 无限制性：KL散度的值可能为无穷大，即当真实分布中的某个事件在理论分布中的概率为0时，KL散度的值为无穷大。

KL散度的计算公式如下：

$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}$$

其中，(P)和(Q)分别为两个概率分布，(P(i))和(Q(i))分别表示在位置(i)处的概率值。当KL散度等于0时，表示两个概率分布完全相同；当KL散度大于0时，表示两个概率分布存在差异，且值越大差异越大。

• 在机器学习中，KL散度有广泛的应用，例如用于衡量两个概率分布之间的差异，或者用于优化生成式模型的损失函数等。此外，KL散度还可以用于基于KL散度的样本选择来有效训练支持向量机（SVM）等算法，以解决SVM在大型数据集合上效率低下的问题。

逻辑回归构造模板

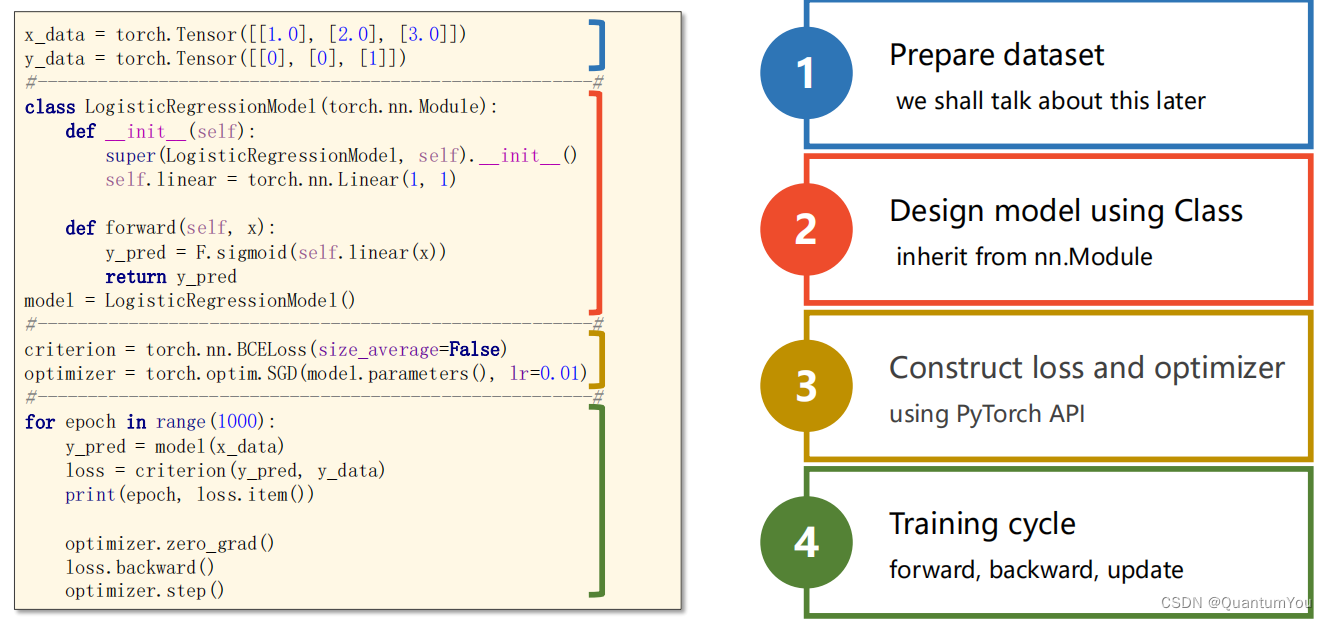
二、处理多维特征的输入

1、逻辑回归模型流程

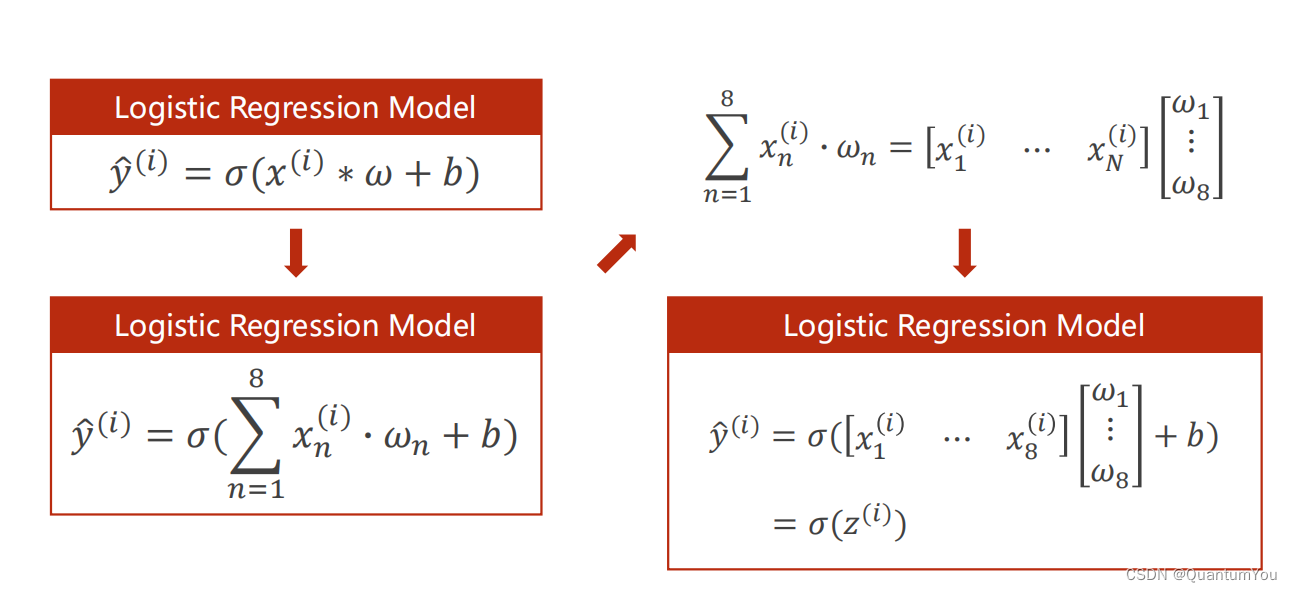
2、Mini-Batch (N samples)

在数学上转化为矩阵运算，转化为向量形式利于GPU进行并行运算

self.linear torch.nn.Linear (8,1) 输入为8，输出为1

说明：

• 1、乘的权重(w)都一样，加的偏置(b)也一样。b变成矩阵时使用广播机制。神经网络的参数w和b是网络需要学习的，其他是已知的。

• 2、学习能力越强，有可能会把输入样本中噪声的规律也学到。我们要学习数据本身真实数据的规律，学习能力要有泛化能力。

• 3、该神经网络共3层；第一层是8维到6维的非线性空间变换，第二层是6维到4维的非线性空间变换，第三层是4维到1维的非线性空间变换。
  

• 4、本算法中torch.nn.Sigmoid() 将其看作是网络的一层，而不是简单的函数使用

torch.sigmoid、torch.nn.Sigmoid和torch.nn.functional.sigmoid的区别

三、加载数据集

• DataLoader 主要加载数据集

说明：

• 1、DataSet 是抽象类，不能实例化对象，主要是用于构造我们的数据集

• 2、DataLoader 需要获取DataSet提供的索引[i]和len;用来帮助我们加载数据，比如说做shuffle(提高数据集的随机性)，batch_size,能拿出Mini-Batch进行训练。它帮我们自动完成这些工作。DataLoader可实例化对象。
  

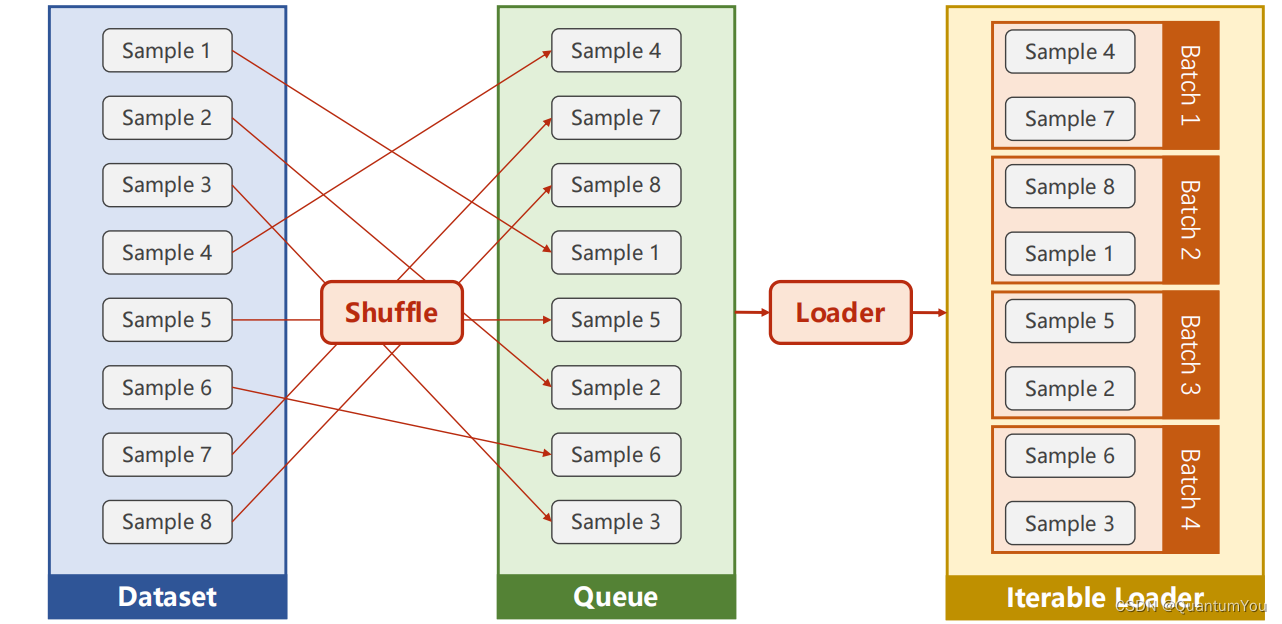
• 3、__getitem__目的是为支持下标(索引)操作

1、Python 魔法方法介绍

• 在Python中，有一些特殊的方法（通常被称为“魔法方法”或“双下划线方法”）是由Python解释器预定义的，它们允许对象进行某些特殊的操作或重载常见的运算符。这些魔法方法通常以双下划线（__）开始和结束。

1. 初始化方法：__init__(self, ...)

在创建对象时自动调用，用于初始化对象的状态。

class MyClass:
    def __init__(self, value):
        self.value = value

2. 字符串表示方法：__str__(self) 和 __repr__(self)

用于定义对象的字符串表示。__str__用于在print函数中，而__repr__用于在repr函数中。

class MyClass:
    def __init__(self, value):
        self.value = value
    
    def __str__(self):
        return f"MyClass({self.value})"
    
    def __repr__(self):
        return f"MyClass({self.value})"

3. 比较方法：如 __eq__(self, other)、__lt__(self, other) 等

用于定义对象之间的比较操作。

class MyClass:
    def __init__(self, value):
        self.value = value
    
    def __eq__(self, other):
        if isinstance(other, MyClass):
            return self.value == other.value
        return False

4. 算术运算符方法：如 __add__(self, other)、__sub__(self, other) 等

用于定义对象之间的算术运算。

class MyClass:
    def __init__(self, value):
        self.value = value
    
    def __add__(self, other):
        if isinstance(other, MyClass):
            return MyClass(self.value + other.value)
        return NotImplemented

5. 容器方法：如 __len__(self)、__getitem__(self, key)、__setitem__(self, key, value) 等

• 用于定义对象作为容器（如列表、字典等）时的行为。

• 每个魔法方法是python的内置方法。方法都有对应的内置函数，或者运算符，对这个对象使用这些函数或者运算符时就会调用类中的对应魔法方法，可以理解为重写这些python的内置函数

2、Epoch，Batch-Size，Iteration区别

eg:

10,000 examples --> 1000 Batch-size --> 10 Iteration

1、需要mini_batch 就需要import DataSet和DataLoader

2、继承DataSet的类需要重写init，getitem,len魔法函数。分别是为了加载数据集，获取数据索引，获取数据总量。

3、DataLoader对数据集先打乱(shuffle)，然后划分成mini_batch。

4、len函数的返回值 除以 batch_size 的结果就是每一轮epoch中需要迭代的次数。

5、inputs, labels = data中的inputs的shape是[32,8],labels 的shape是[32,1]。也就是说mini_batch在这个地方体现的

在windows 下 wrap 和 linux 下 fork 代码优化

3、加载相关数据集的实现

import  torch
import  numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader

 
class DiabetesDataset(Dataset):
    def __init__(self,filepath):
        xy = np.loadtxt(filepath,delimiter=',',dtype=np.float32)
        #shape本身是一个二元组（x,y）对应数据集的行数和列数，这里[0]我们取行数,即样本数
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])

    def __getitem__(self, index):
        return self.x_data[index],self.y_data[index]

    def __len__(self):
        return self.len
        
#定义好DiabetesDataset后我们就可以实例化他了
dataset = DiabetesDataset('./data/Diabetes_class.csv.gz')
#我们用DataLoader为数据进行分组，batch_size是一个组中有多少个样本，shuffle表示要不要对样本进行随机排列
#一般来说，训练集我们随机排列，测试集不。num_workers表示我们可以用多少进程并行的运算
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)

class Model(torch.nn.Module):
    def __init__(self):#构造函数
        super(Model,self).__init__()
        self.linear1 = torch.nn.Linear(8,6)#8维到6维
        self.linear2 = torch.nn.Linear(6, 4)#6维到4维
        self.linear3 = torch.nn.Linear(4, 1)#4维到1维
        self.sigmoid = torch.nn.Sigmoid()#因为他里边也没有权重需要更新，所以要一个就行了，单纯的算个数


    def forward(self, x):#构建一个计算图，就像上面图片画的那样
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return  x

model = Model()#实例化模型

criterion = torch.nn.BCELoss(size_average=False)
#model.parameters()会扫描module中的所有成员，如果成员中有相应权重，那么都会将结果加到要训练的参数集合上
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)#lr为学习率

if __name__=='__main__':#if这条语句在windows系统下一定要加，否则会报错
    for epoch in range(1000):
        for i,data in enumerate(train_loader,0):#取出一个bath
            # repare data
            inputs,labels = data#将输入的数据赋给inputs，结果赋给labels 
            #Forward
            y_pred = model(inputs)
            loss = criterion(y_pred,labels)
            print(epoch,loss.item())
            #Backward
            optimizer.zero_grad()
            loss.backward()
            #update
            optimizer.step()

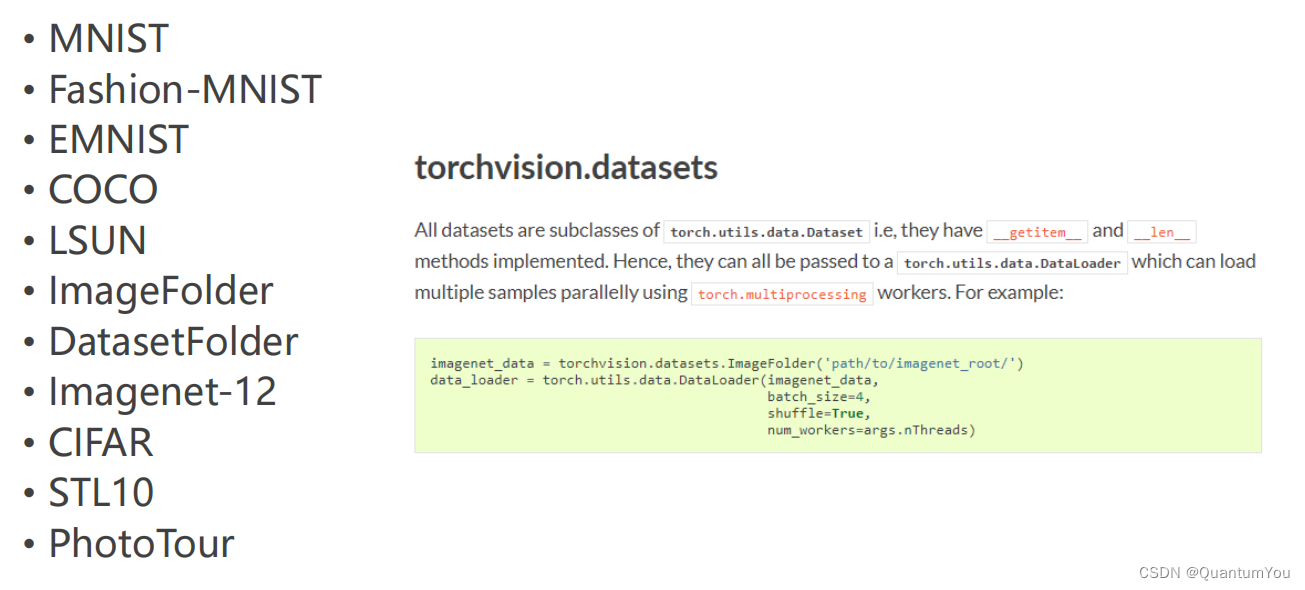
4、在torchvision,datasets数据集

在torchvision,datasets 下的常见数据集

四、多分类问题

1、softmax 再探究

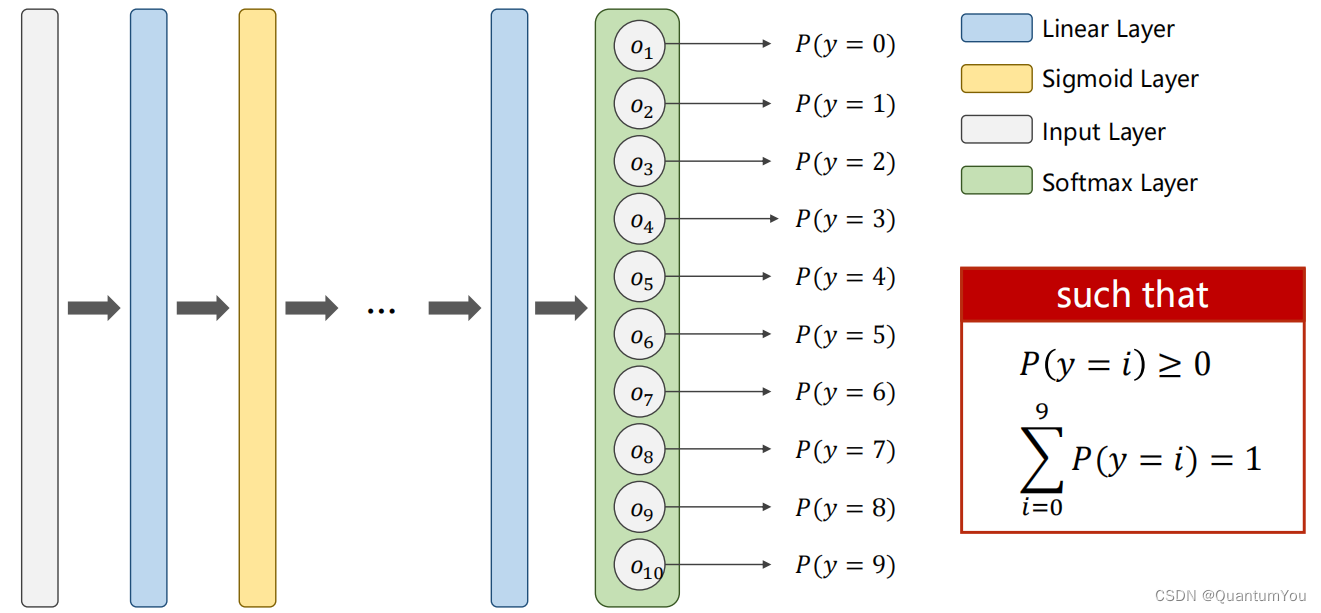
每个类别输出都使用二分类的交叉熵，这样的话所有类别都是一个独立的分布，概率加起来不等于一

注意：我们是将每一个类别看作一个二分类问题，且最后每个输出值需满足两个要求：①≥ 0 ②∑ = 1 即输出的是一个分布。

在神经网络中，特别是在分类任务中，Softmax 函数通常被用作最后一层（线性层或全连接层）的激活函数，以将模型的输出转换为概率分布。对于给定向

$$\text{Softmax}(Z^l{)}_i=\frac{e^{Z_i^l}}{{\sum }_{j=1}^k{e}^{Z_j^l}}$$$$\text{对于}i=0\dots \dots K-1$$

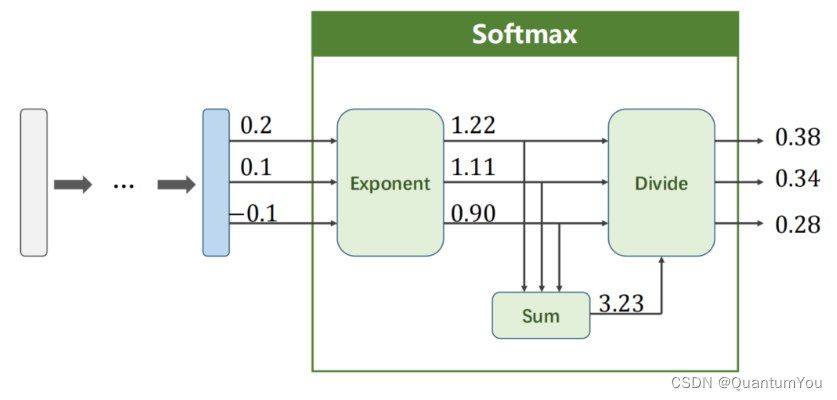
除法是因为归一化

因为输出的是概率，所以要是正数；k个类的概率相互抑制，概率之和是1.所以要先转正再归一化，也就是softmax

• 在分类任务中，特别是当使用交叉熵损失函数（Cross-Entropy Loss）时，对于给定的预测概率分布 $$\hat{Y}$$和真实标签 Y，损失函数可以定义为：

$$\text{Loss}(\hat{Y},Y)=-\sum _{i=1}^k{Y}_i\log {\hat{Y}}_i$$

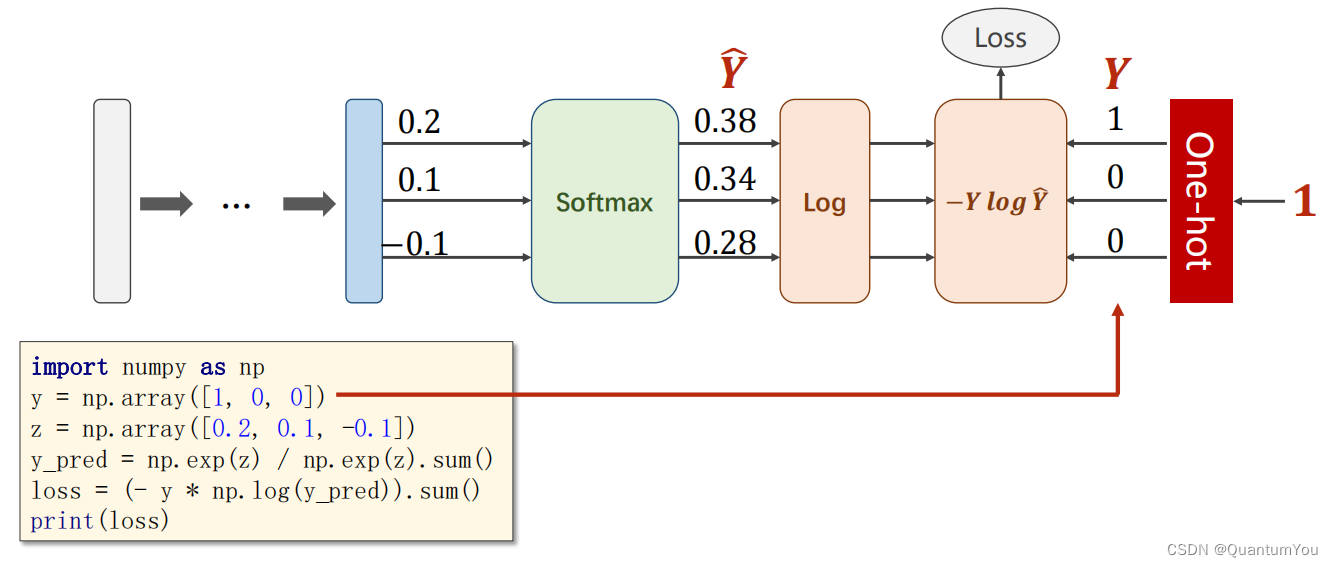
注意这里，(Y) 通常是一个独热编码（one-hot encoded）的向量，其中只有一个元素为1（表示真实的类别），其余元素为0。因此，在实际计算中，由于除了真实类别对应的 (Y_i) 为1外，其余 (Y_i) 都为0，所以求和式中实际上只有一项是有效的。

2、独热编码问题

one-hot介绍

五、语言模型初步理解

1、语言模型的概念

• 语言模型（language model）是自然语言处理的重要技术。自然语言处理中最常见的数据是文本数据。可以把一段自然语言文本看作一段离散的时间序列。假设一段长度为$T$的文本中的词依次为$w_1,w_2,\dots ,w_T$，那么在离散的时间序列中，$w_t$（$1\le t\le T$）可看作在时间步（time step）$t$的输出或标签。给定一个长度为$T$的词的序列$w_1,w_2,\dots ,w_T$，语言模型将计算该序列的概率：

$$P(w_1,w_2,\dots ,w_T).$$

2、语言模型的计算

• 假设序列$w_1,w_2,\dots ,w_T$中的每个词是依次生成的，我们有

$$P(w_1,w_2,\dots ,w_T)=\prod _{t=1}^{T}P(w_t\mid w_1,\dots ,w_{t-1}).$$

例如，一段含有4个词的文本序列的概率

$$P(w_1,w_2,w_3,w_4)=P(w_1)P(w_2\mid w_1)P(w_3\mid w_1,w_2)P(w_4\mid w_1,w_2,w_3).$$

• 为了计算语言模型，我们需要计算词的概率，以及一个词在给定前几个词的情况下的条件概率，即语言模型参数。设训练数据集为一个大型文本语料库，如维基百科的所有条目。词的概率可以通过该词在训练数据集中的相对词频来计算。例如，$P(w_1)$可以计算为$w_1$在训练数据集中的词频（词出现的次数）与训练数据集的总词数之比。因此，根据条件概率定义，一个词在给定前几个词的情况下的条件概率也可以通过训练数据集中的相对词频计算。例如，$P(w_2\mid w_1)$可以计算为$w_1,w_2$两词相邻的频率与$w_1$词频的比值，因为该比值即$P(w_1,w_2)$与$P(w_1)$之比；而$P(w_3\mid w_1,w_2)$同理可以计算为$w_1$、$w_2$和$w_3$三词相邻的频率与$w_1$和$w_2$两词相邻的频率的比值。以此类推。

3、 $n$元语法

• 当序列长度增加时，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。$n$元语法通过马尔可夫假设（虽然并不一定成立）简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面$n$个词相关，即$n$阶马尔可夫链（Markov chain of order $n$）。如果$n=1$，那么有$P(w_3\mid w_1,w_2)=P(w_3\mid w_2)$。如果基于$n-1$阶马尔可夫链，我们可以将语言模型改写为

$$P(w_1,w_2,\dots ,w_T)\approx \prod _{t=1}^{T}P(w_t\mid w_{t-(n-1)},\dots ,w_{t-1}).$$

以上也叫$n$元语法（$n$-grams）。它是基于$n-1$阶马尔可夫链的概率语言模型。当$n$分别为1、2和3时，我们将其分别称作一元语法（unigram）、二元语法（bigram）和三元语法（trigram）。例如，长度为4的序列$w_1,w_2,w_3,w_4$在一元语法、二元语法和三元语法中的概率分别为

$$\begin{array}{rl}P(w_1,w_2,w_3,w_4)& =P(w_1)P(w_2)P(w_3)P(w_4),\\ P(w_1,w_2,w_3,w_4)& =P(w_1)P(w_2\mid w_1)P(w_3\mid w_2)P(w_4\mid w_3),\\ P(w_1,w_2,w_3,w_4)& =P(w_1)P(w_2\mid w_1)P(w_3\mid w_1,w_2)P(w_4\mid w_2,w_3).\end{array}$$

当$n$较小时，$n$元语法往往并不准确。例如，在一元语法中，由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而，当$n$较大时，$n$元语法需要计算并存储大量的词频和多词相邻频率。

六、相关代码实现

1、简易实现小项目代码地址

Github

https://github.com/aqlzh/Artificial-intelligence

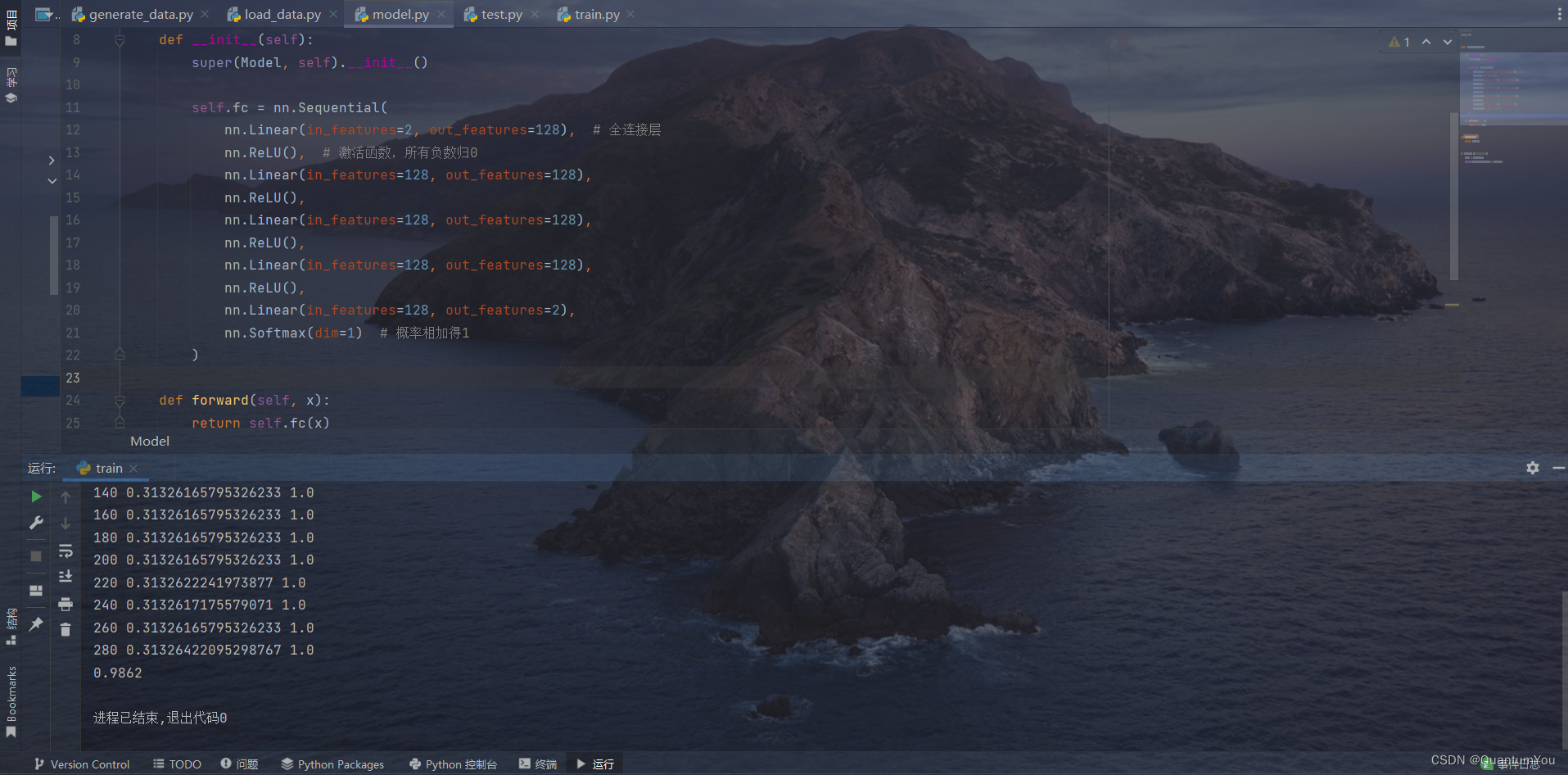
2、简易实现小项目运行过程

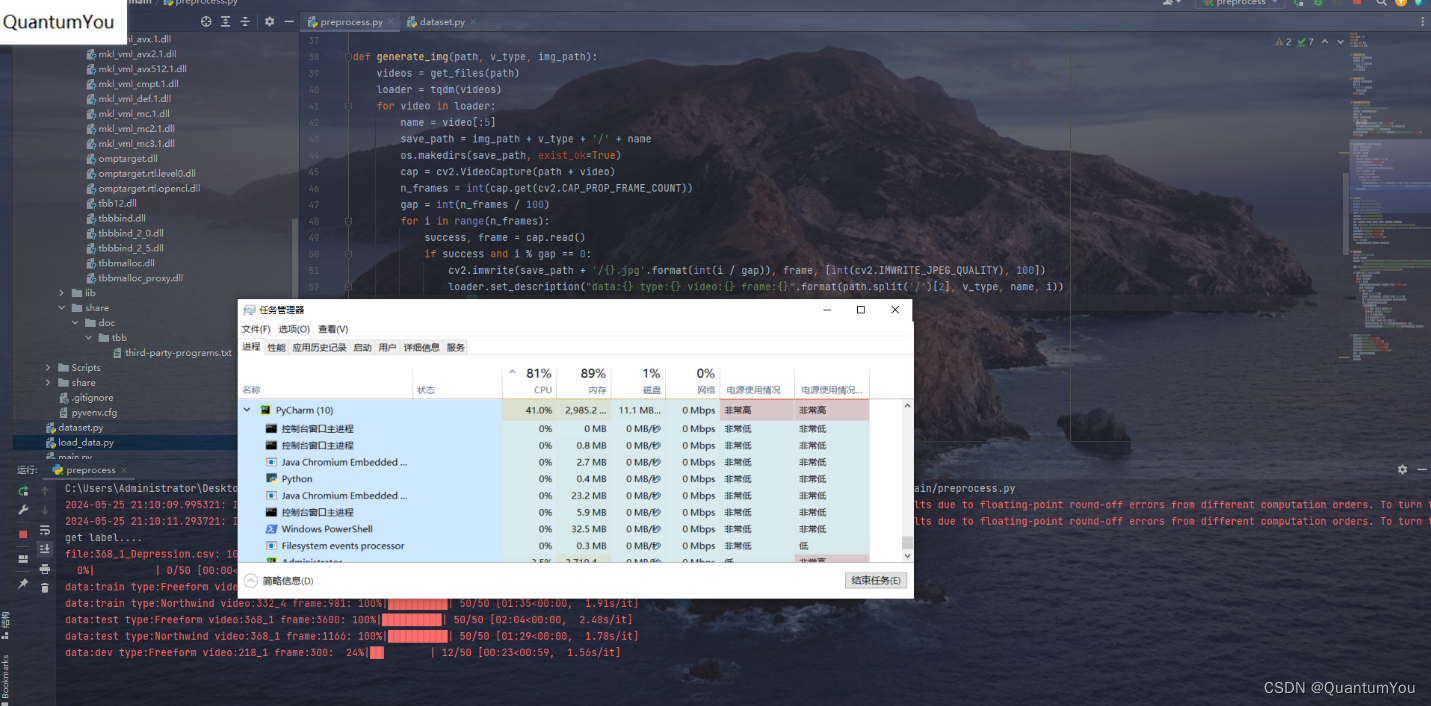
3、抑郁症数据预处理运行过程

def get_files(path):
    file_info = os.walk(path)
    file_list = []
    for r, d, f in file_info:
        file_list += f
    return file_list


def get_dirs(path):
    file_info = os.walk(path)
    dirs = []
    for d, r, f in file_info:
        dirs.append(d)
    return dirs[1:]


def generate_label_file():
    print('get label....')
    base_url = './AVEC2014/label/DepressionLabels/'
    file_list = get_files(base_url)
    labels = []
    loader = tqdm(file_list)
    for file in loader:
        label = pd.read_csv(base_url + file, header=None)
        labels.append([file[:file.find('_Depression.csv')], label[0][0]])
        loader.set_description('file:{}'.format(file))
    pd.DataFrame(labels, columns=['file', 'label']).to_csv('./processed/label.csv', index=False)
    return labels


def generate_img(path, v_type, img_path):
    videos = get_files(path)
    loader = tqdm(videos)
    for video in loader:
        name = video[:5]
        save_path = img_path + v_type + '/' + name
        os.makedirs(save_path, exist_ok=True)
        cap = cv2.VideoCapture(path + video)
        n_frames = int(cap.get(cv2.CAP_PROP_FRAME_COUNT))
        gap = int(n_frames / 100)
        for i in range(n_frames):
            success, frame = cap.read()
            if success and i % gap == 0:
                cv2.imwrite(save_path + '/{}.jpg'.format(int(i / gap)), frame, [int(cv2.IMWRITE_JPEG_QUALITY), 100])
                loader.set_description("data:{} type:{} video:{} frame:{}".format(path.split('/')[2], v_type, name, i))
        cap.release()


def get_img():
    print('get video frames....')
    train_f = './AVEC2014/train/Freeform/'
    train_n = './AVEC2014/train/Northwind/'
    test_f = './AVEC2014/test/Freeform/'
    test_n = './AVEC2014/test/Northwind/'
    validate_f = './AVEC2014/dev/Freeform/'
    validate_n = './AVEC2014/dev/Northwind/'
    dirs = [train_f, train_n, test_f, test_n, validate_f, validate_n]
    types = ['Freeform', 'Northwind', 'Freeform', 'Northwind', 'Freeform', 'Northwind']
    img_path = ['./img/train/', './img/train/', './img/test/', './img/test/', './img/validate/', './img/validate/']
    os.makedirs('./img/train', exist_ok=True)
    os.makedirs('./img/test', exist_ok=True)
    os.makedirs('./img/validate', exist_ok=True)
    for i in range(6):
        generate_img(dirs[i], types[i], img_path[i])


def get_face():
    print('get frame faces....')
    detector = MTCNN()
    save_path = ['./processed/train/Freeform/', './processed/train/Northwind/', './processed/test/Freeform/',
                 './processed/test/Northwind/', './processed/validate/Freeform/', './processed/validate/Northwind/']
    paths = ['./img/train/Freeform/', './img/train/Northwind/', './img/test/Freeform/', './img/test/Northwind/',
             './img/validate/Freeform/', './img/validate/Northwind/']
    for index, path in enumerate(paths):
        dirs = get_dirs(path)
        loader = tqdm(dirs)
        for d in loader:
            os.makedirs(save_path[index] + d.split('/')[-1], exist_ok=True)
            files = get_files(d)
            for file in files:
                img_path = d + '/' + file
                s_path = save_path[index] + d.split('/')[-1] + '/' + file
                img = cv2.cvtColor(cv2.imread(img_path), cv2.COLOR_BGR2RGB)
                info = detector.detect_faces(img)
                if (len(info) > 0):
                    x, y, width, height = info[0]['box']
                    confidence = info[0]['confidence']
                    b, g, r = cv2.split(img)
                    img = cv2.merge([r, g, b])
                    img = img[y:y + height, x:x + width, :]
                    cv2.imwrite(s_path, img, [int(cv2.IMWRITE_JPEG_QUALITY), 100])
                    loader.set_description('confidence:{:4f} img:{}'.format(confidence, img_path))


if __name__ == '__main__':
    os.makedirs('./img', exist_ok=True)
    os.makedirs('./processed', exist_ok=True)
    os.makedirs('./processed/train', exist_ok=True)
    os.makedirs('./processed/test', exist_ok=True)
    os.makedirs('./processed/validate', exist_ok=True)
    label = generate_label_file()
    get_img()
    get_face()

数据预处理时间最长的一集 😢😢

预处理有两步骤

• 第一步是从视频中提取图片（抽取视频帧，每个视频按间隔抽取100-105帧）
• 第二步是从图片中提取人脸信息（使用MTCNN提取人脸，并分割图片）
  

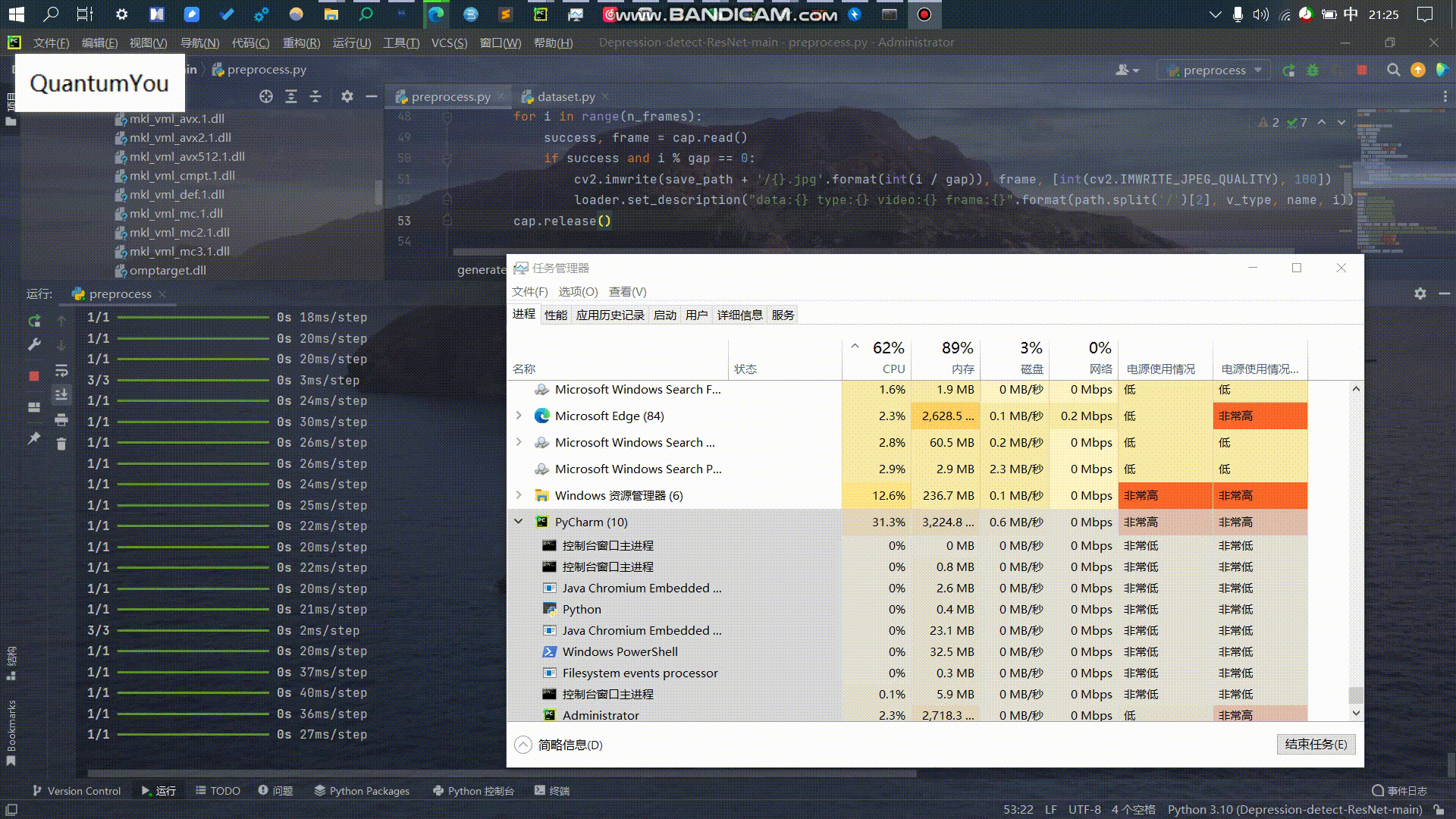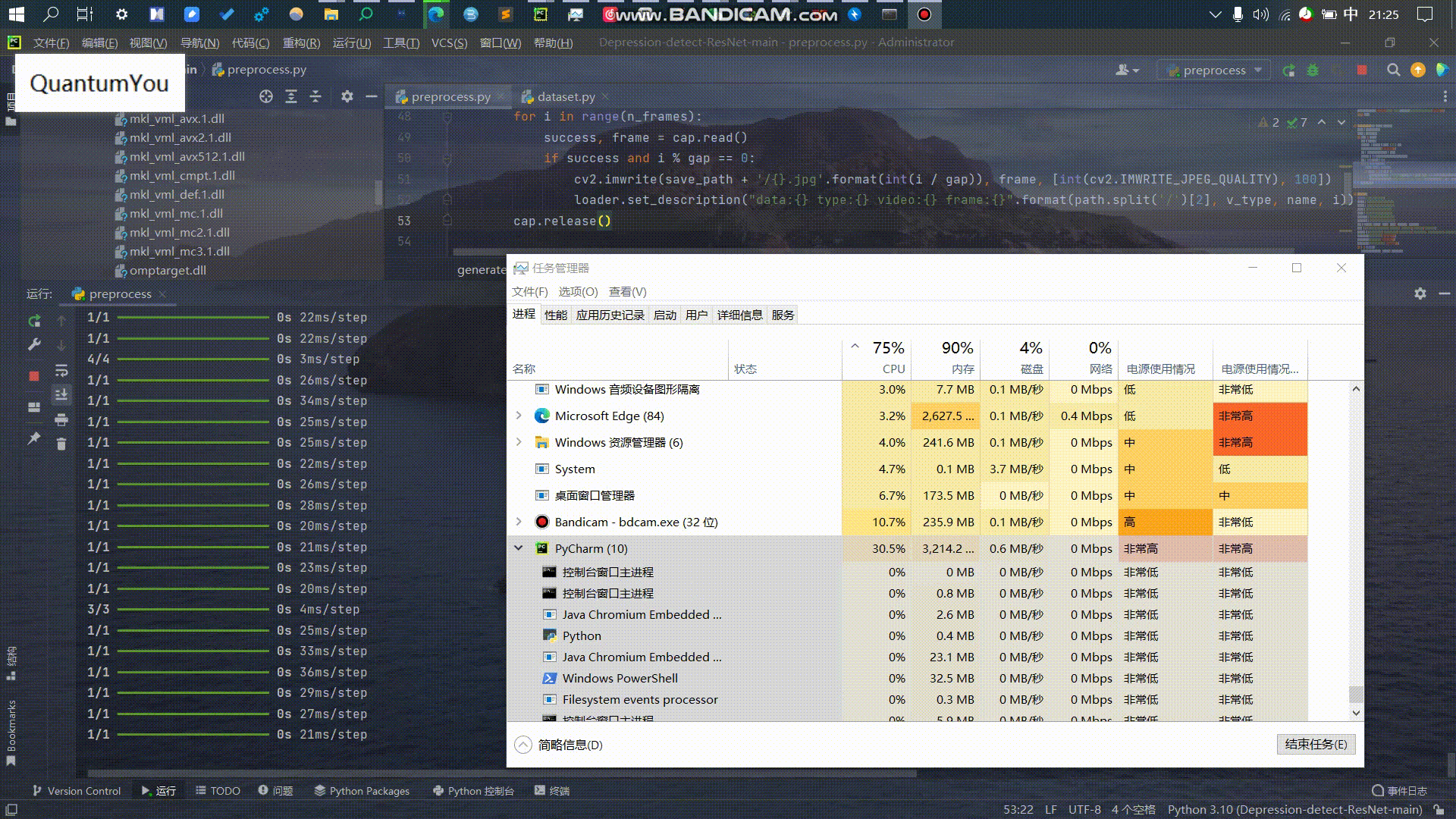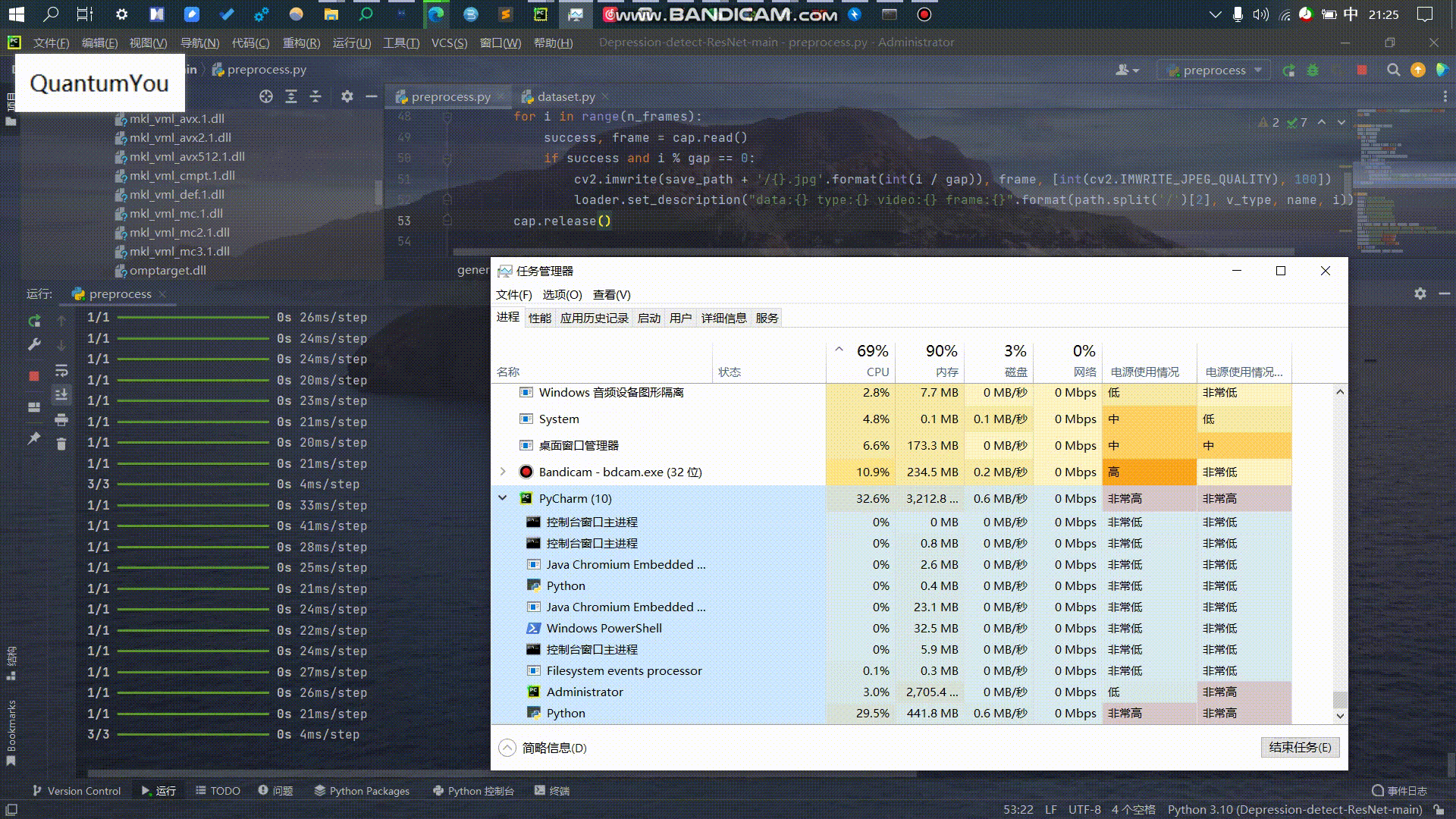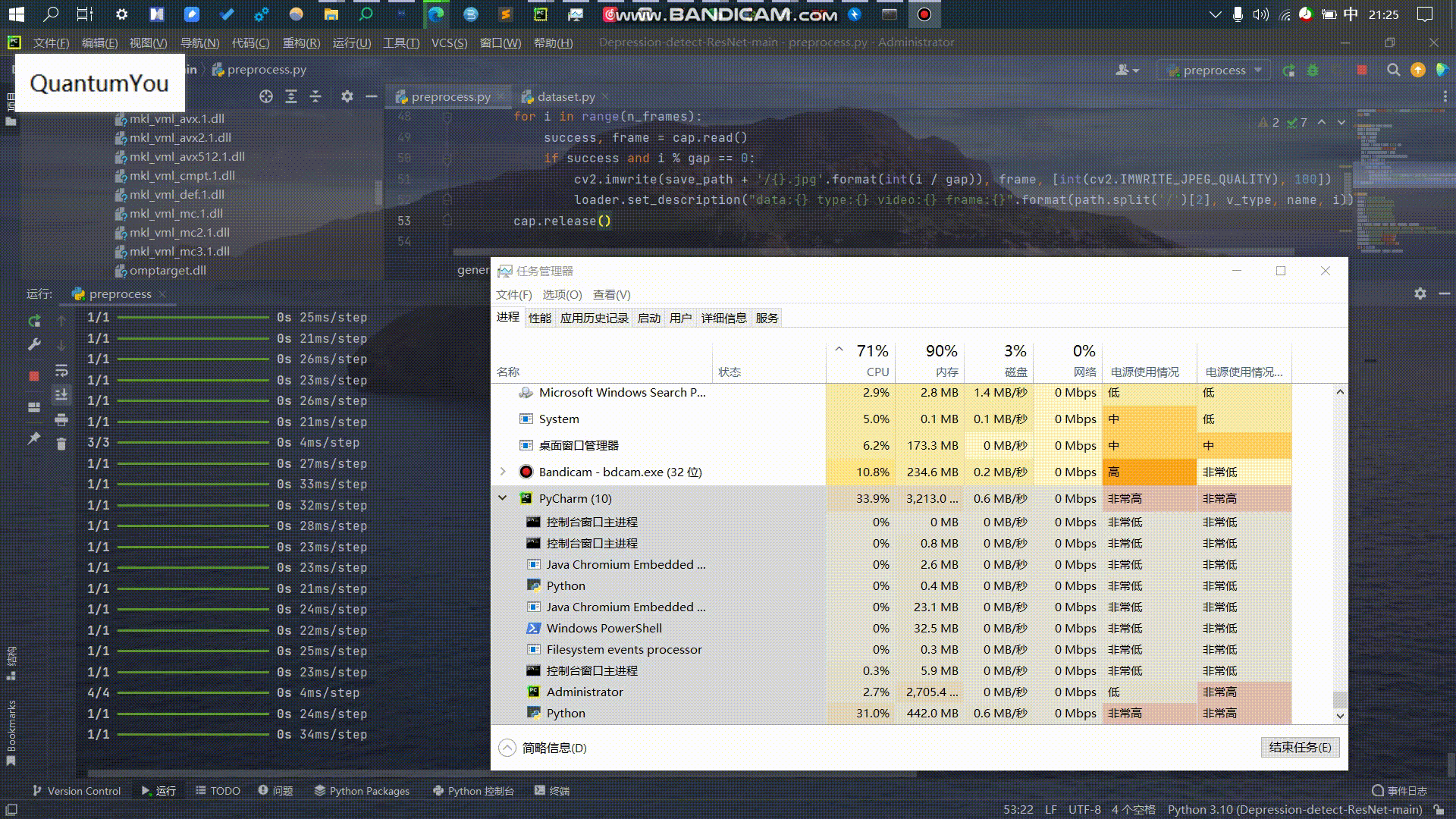
预处理数据成功，结果如下（跑了一整个晚上）😵😵

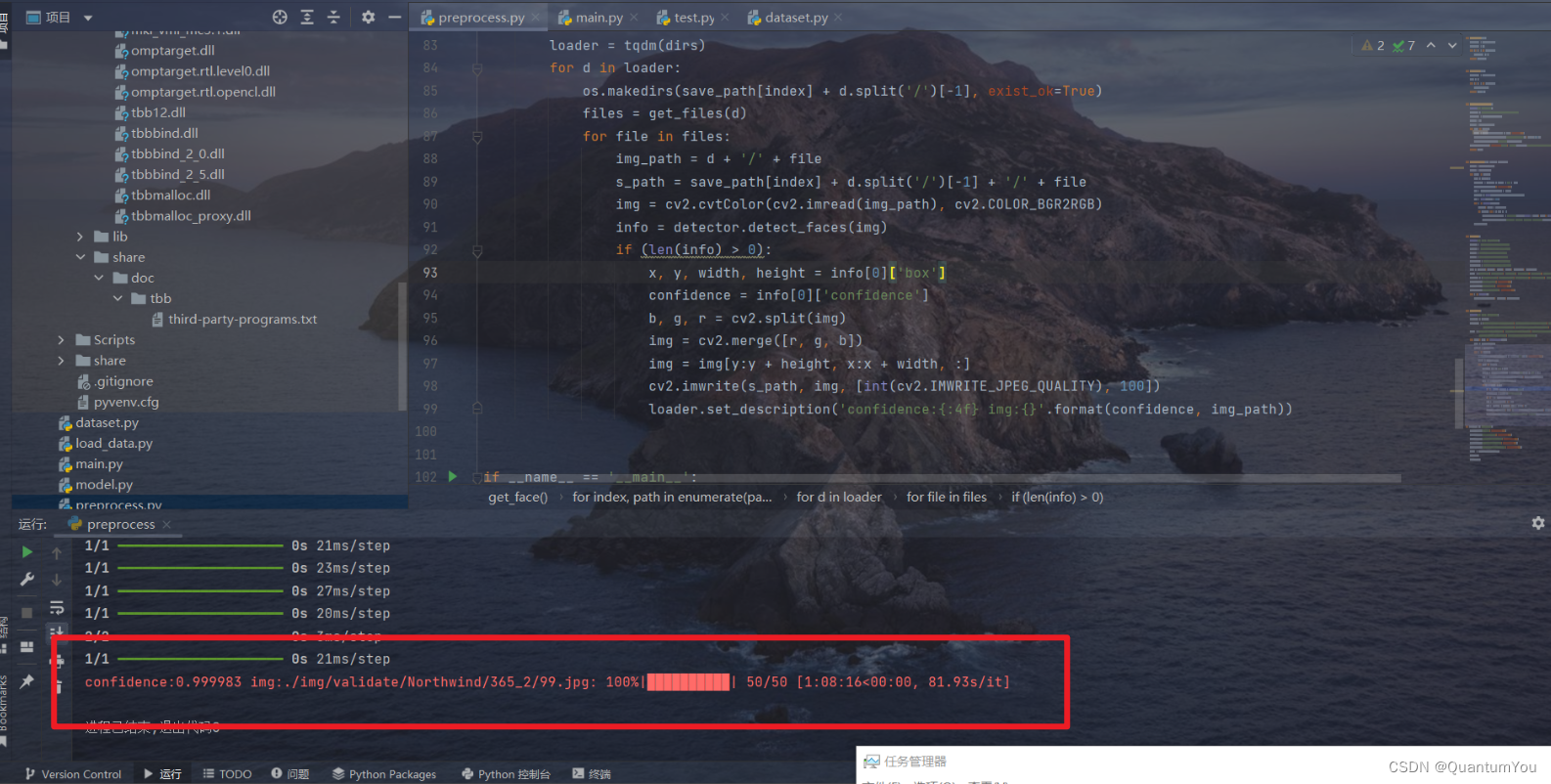
4、抑郁症数据训练运行过程

电脑配置感觉跟不上了，跑不动了，epoch 0 都跑了大半天😱😱

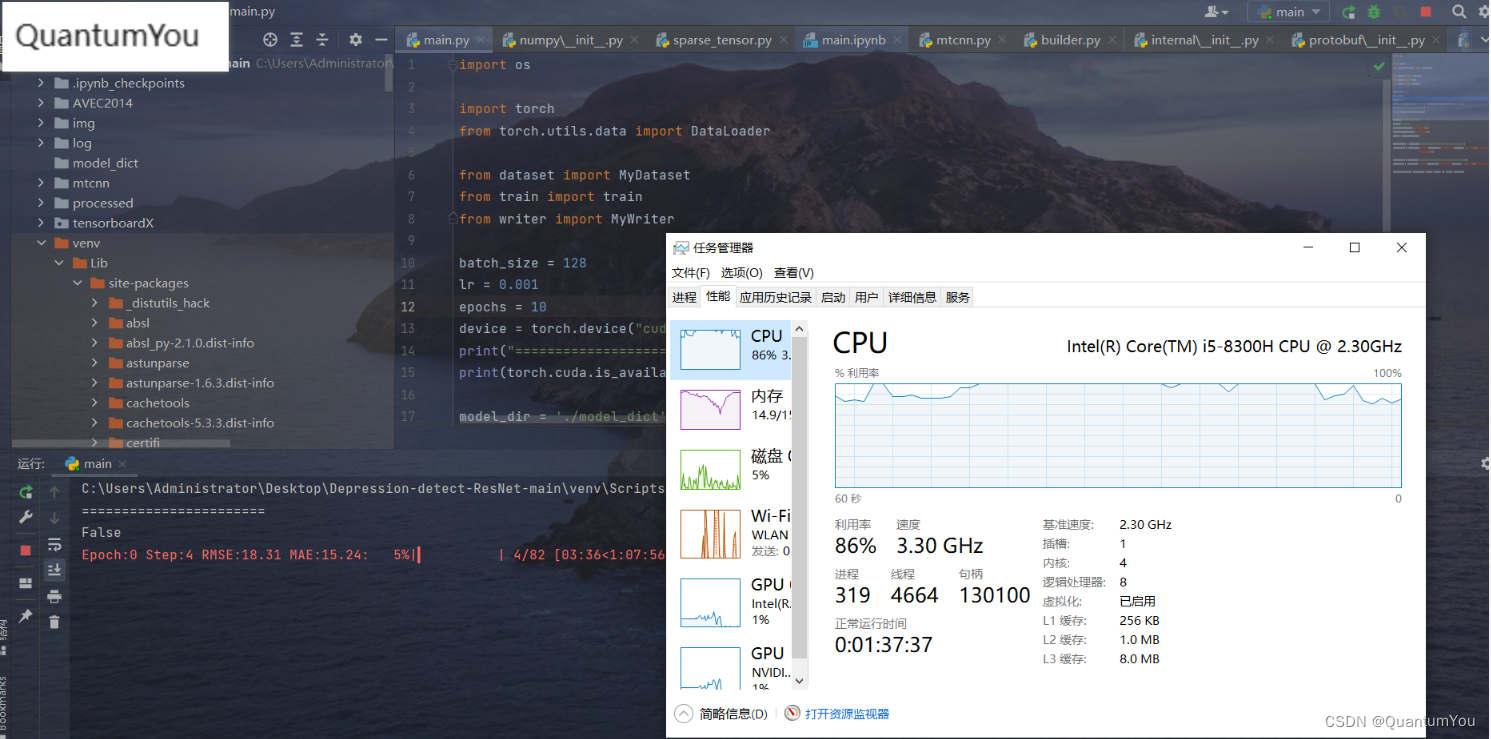
七、遇到问题及其解决方案

1、pycharm 不能使用GPU加速训练

https://blog.csdn.net/QuantumYou/article/details/139215013?spm=1001.2014.3001.5501

2、google.protobuf.internal冲突问题

https://blog.csdn.net/QuantumYou/article/details/139212458?spm=1001.2014.3001.5501