99.恢复二叉搜索树
1、题目描述
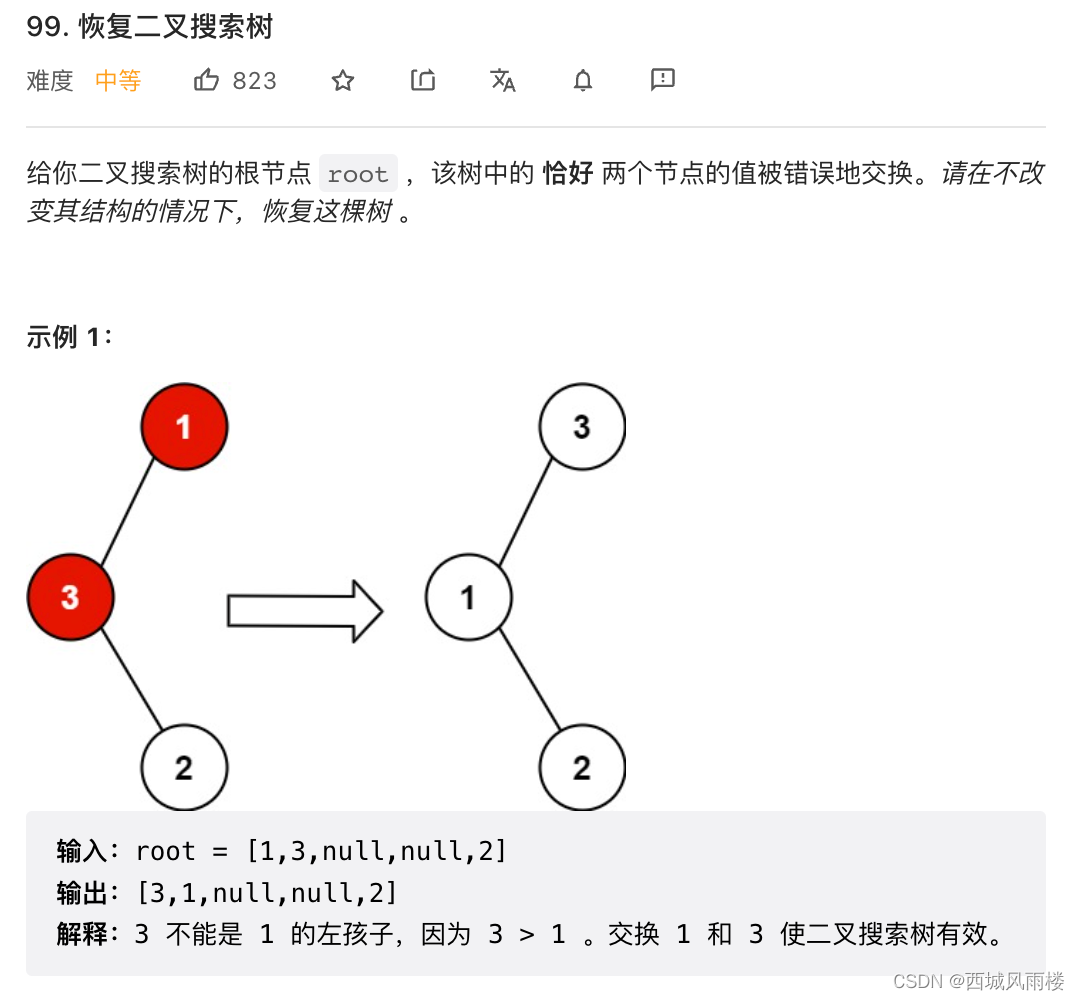
题目的额外要求是: 使用
O(n)空间复杂度的解法很容易实现。你能想出一个只使用O(1)空间的解决方案吗?
2、解题思路
二叉搜索树中某两个节点被交换了数值,那么对中序序列的影响如下:
- 假设没有交换之前二叉搜索树的中序序列为:[1, 2, 3, 4, 5]
- 因为交换只发生一次,因此这次交换要么是相邻的要么是不相邻的,比如交换3和4之后得到[1, 2, 4, 3, 5],交换2和4得到[1, 4, 3, 2, 5]
最直接的想法就是,在二叉搜索树中找到被交换的两个节点,然后将二者的数值直接换回来即可,但是如何找到二叉搜索树中被交换了值的两个节点呢?
仔细观察相邻交换和不相邻交换构成的序列,我们很容易发现相邻交换只会在中序序列中产生一个逆序对,而不相邻交换则会产生两个。根据这个特点,解题思路来了:
- 采用中序遍历的方式遍历整棵二叉树,同时声明两个指针pre和cur
- pre指向cur在中序序列中的前一个节点,cur指向当前正在访问的中序序列中的节点
- 如果pre的值比cur大,说明发现了一个逆序对,那么记录这个逆序对,同时记录当前发现的逆序对的数目
- 如果整棵树遍历结束,发现逆序对的数目是1,说明只发生了相邻交换,这个时候只需要将发现的第一个逆序对的数值交换
- 如果发现逆序对的数目是2,说明发生的是非相邻交换,那么只需要将第一个逆序对的第一个节点和第二个逆序对的第二个节点进行交换
如果采用递归的方式遍历整棵树,空间复杂度肯定是O(N),因为借助了系统栈,如果采用栈的方式迭代,和直接递归没什么差别,那么我们很容易想到第三种遍历方式,那就是Morris遍历,Morris遍历时间复杂度是O(N),空间复杂度是O(1),刚好符合要求。
3、解题代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private static class Pair {
private TreeNode first;
private TreeNode second;
}
public void recoverTree(TreeNode root) {
TreeNode cur = root;
TreeNode pre = null;
Pair[] pairs = new Pair[2];
pairs[0] = new Pair();
pairs[1] = new Pair();
int reversePairNum = 0;
while (cur != null) {
if (cur.left != null) {
TreeNode mostRight = cur.left;
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right != cur) {
// 说明是第一次到来这个
mostRight.right = cur;
cur = cur.left;
continue;
}
// 说明是第二次到达这个地方
// 需要判断pre和cur的情况了
mostRight.right = null;
}
if (pre != null) {
if (pre.val > cur.val) {
// 发现了第一对逆序对
reversePairNum++;
if (reversePairNum == 1) {
pairs[0].first = pre;
pairs[0].second = cur;
} else {
pairs[1].first = pre;
pairs[1].second = cur;
}
}
}
pre = cur;
cur = cur.right;
}
if (reversePairNum == 1) {
int tmp = pairs[0].first.val;
pairs[0].first.val = pairs[0].second.val;
pairs[0].second.val = tmp;
} else {
int tmp = pairs[0].first.val;
pairs[0].first.val = pairs[1].second.val;
pairs[1].second.val = tmp;
}
}
}
4、提交结果