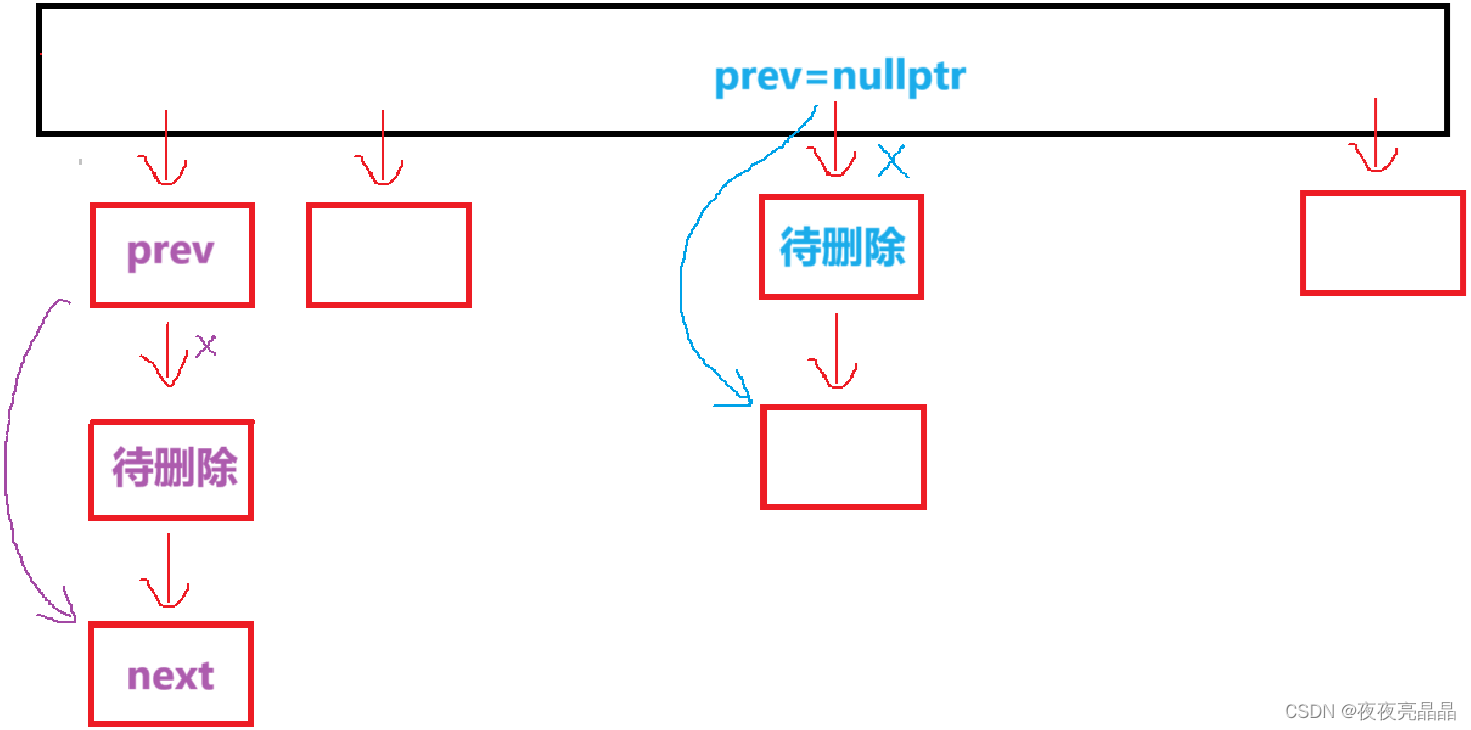
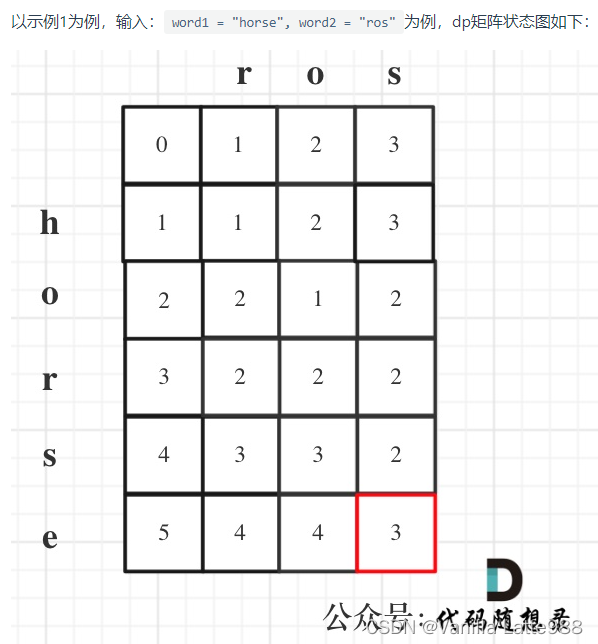
题目

两个随机变量x和y，如果联合PDF分解为：

那么称他们为条件独立的。在上式中z是条件随机变量。

我们观察

其中, , 是相互独立的。证明和是条件独立的。给出条件变量是A。和是无条件独立么？也就是

成立么？为了回答这个问题，考虑, , 是独立且都有PDF N(0,1)

解答

参考（10-7），当A是条件时可以得到：

由独立的性质：

可以到

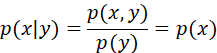
因此当, 是相互独立时，得到：

由于, 是相互独立的，因此：

也就是和是条件独立的

---

如果要验证和是否无条件独立，只需要计算：

由于

因此：

于是：

由, , 是相互独立，因此：

而由于：

因此：

因此：与不独立

---

当然，另外一种逻辑，就是验证是否可以拆成和的乘积形式。

此时考虑：

根据多元高斯分布性质（多元高斯分布（Multivariate Gaussian Distribution）（详细说明，便于理解）-CSDN博客），得到:

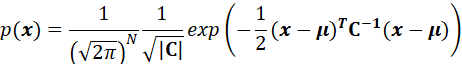
其中：

 

根据上面计算，其中，而：

再利用, 是相互独立，且服从N

因此：

用同样的方式获得后，可以得到：

因此，可以得到：

于是中的可以化简为：

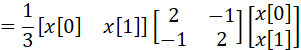
显然，上式无法因式分解成仅包含和的独立项，也就是无法拆分成和的乘积项，因此

不成立。也就是和不是无条件独立