秋招突击——算法——模板题——区间DP（1）—

秋招突击——算法——模板题——区间DP（1）——加分二叉树

news2024/10/7 8:26:21

文章目录

- - - 题目描述
    - 思路分析
    - 实现代码
    - 分析总结

题目描述

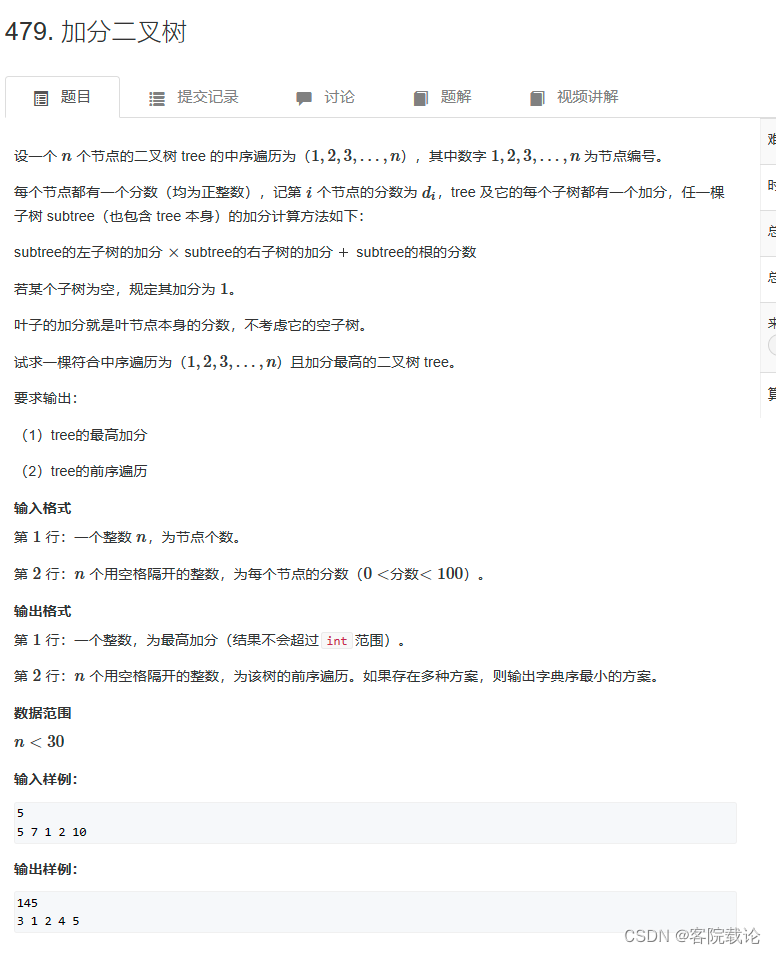
在这里插入图片描述

思路分析

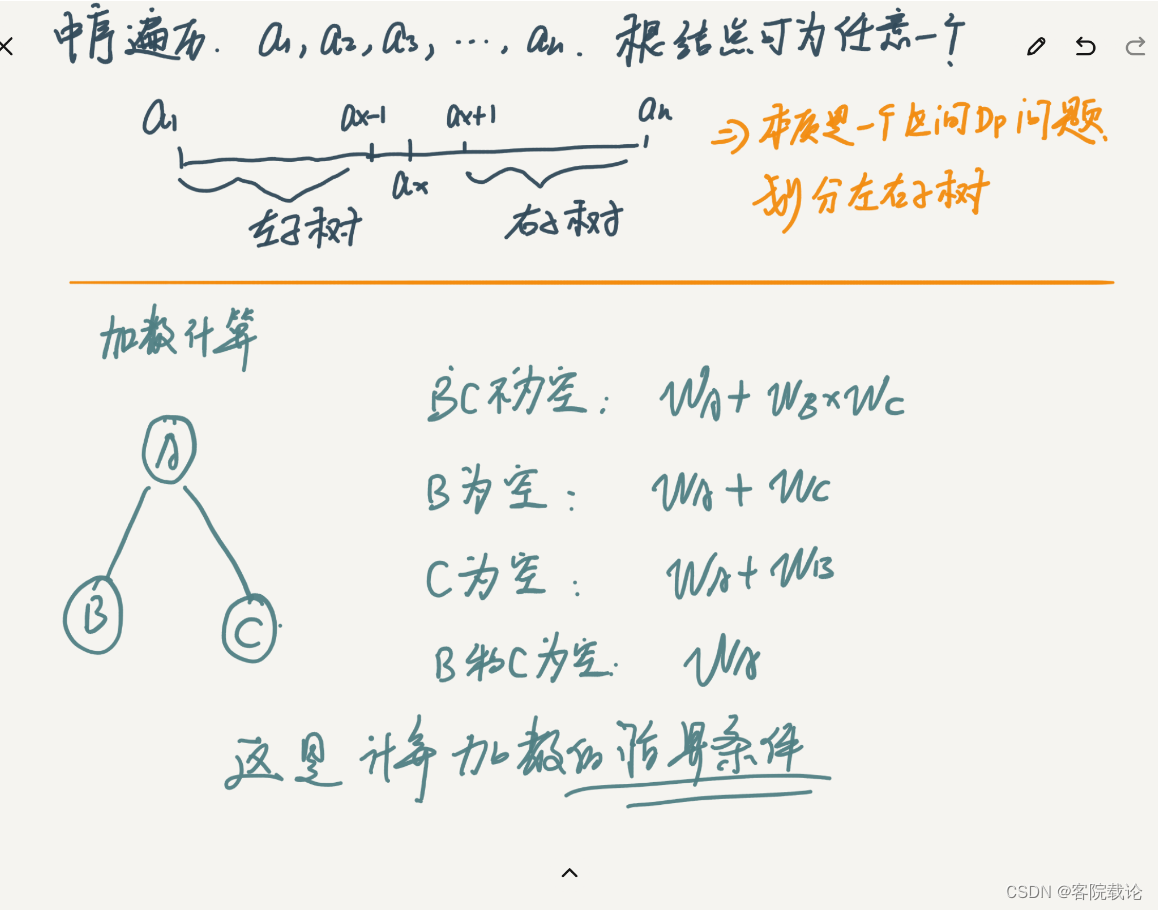
在这里插入图片描述

实现代码

不过我的代码写的真的不够简洁，逻辑不够清晰，后续多练练吧。

// 组合数问题
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 35;
int n,f[N][N],g[N][N],w[N];
// f[i][j]表示区间i到j的构成的二叉树最大的加数
// g[i][j]表示区间i到j的构成最大加数二叉树的根节点的坐标
// w[i]表示第i个节点的权值

void dfs(int l,int r){
    if(l > r) return;
    int k = g[l][r];
    cout<<k<<" ";
    dfs(l,k-1);
    dfs(k + 1,r);

}

int main(){
    cin>>n;
    for(int i = 1;i <= n;i ++) cin>>w[i];

    // 遍历区间的长度
    for (int len = 1; len <= n; ++len) {
        // 遍历区间左端点
        for (int i = 1; i + len - 1 <= n ; ++i) {
            int j = i + len -1;

            // 左右节点相等，不用额外尽心遍历
            if (i == j) f[i][j] = w[i],g[i][j] = i;
            else{
                // 遍历划分节点,总共是三种情况
                for (int k = i; k <= j; ++k) {
                    int score = 0;
                    if (k == i){
                        // 划分节点在左端点，没有左子节点
                        score = w[k] + f[ k + 1][j];
                    }

                    else if (k == j){
                        // 划分节点在右端点，没有右子节点
                        score = w[k] + f[i][k - 1];
                    }

                    else
                    {
                        // 划分节点在中间，左右子节点都有
                        score = w[k] + f[i][k - 1] * f[k + 1][j];
                    }
                    // 记录顶点节点
                    if(f[i][j] < score) {
                        f[i][j] = score;
                        g[i][j] = k;
                    }

                }
            }
        }
    }

    cout<<f[1][n]<<endl;
    dfs(1,n);

};