题目

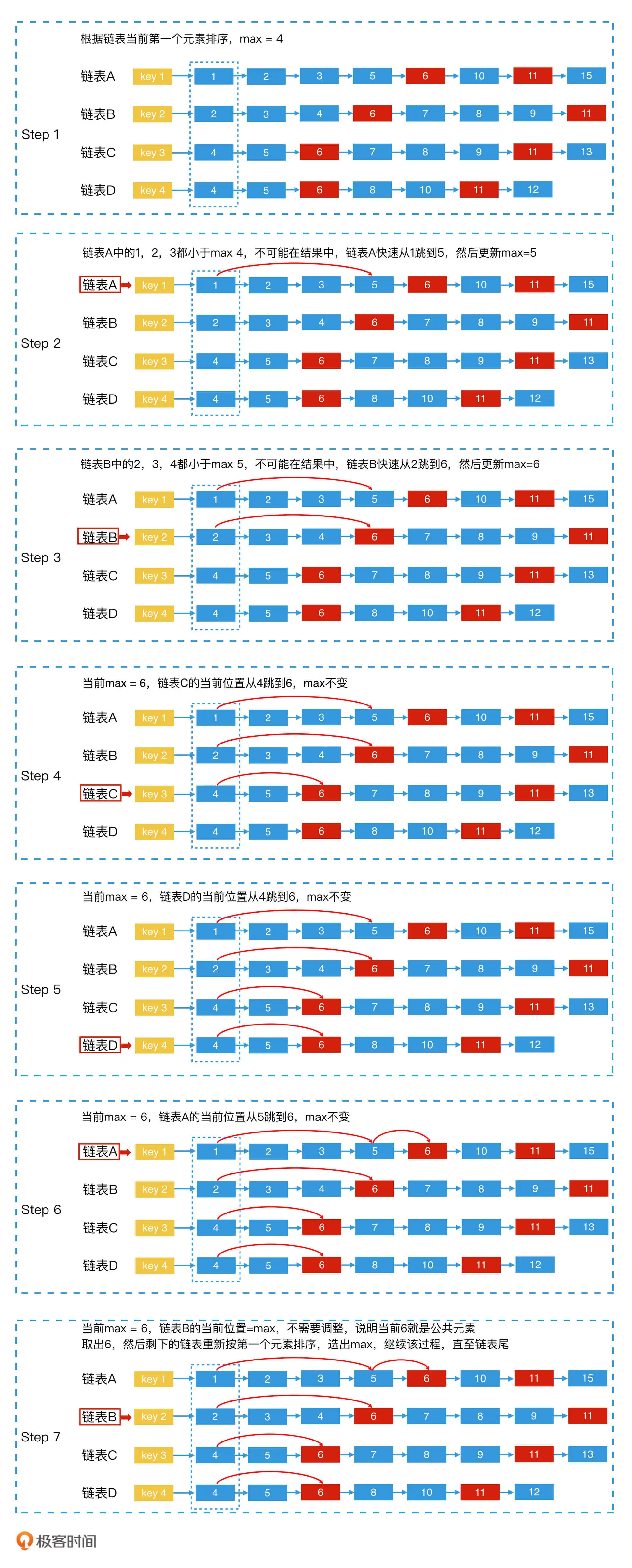
思路

话不多说，直接上代码

附上INT_MAX和INT_MIN

【C++】详解 INT_MAX 和 INT_MIN（INT_MAX 和 INT_MIN是什么？它们的用途是什么？如何防止溢出？）_c++ int max-CSDN博客

代码

/*
leetcode合并石头的最低成本-XMUOJ元素共鸣：深层次的唤醒
--JinlongW-2024/05/26
*/
/*
定义dp[i][j][k]为合并第i堆到第j堆石头为k堆的成本，状态转移方程有关键两点：

1.dp[i][j][1] = dp[i][j][k] + sum(i, j)。不能直接求出合并为1堆的成本，得先合并成k堆。
2.dp[i][j][m] = min(dp[i][p][1] + dp[p + 1][j][m - 1])，i <= p < j，2 <= m <= k。
这里m为堆数，不能直接用k是因为右部分的存在，要对右部分继续划分求解的话，子问题就必须有合并成m堆的情况。
细节：
第一点：一定会有不能合并成1堆的情况，怎么排除掉这种情况呢？
	如果能合并成1堆，就一定得先合并成k堆，这在前面已经讨论过了。这k堆里面的其中1堆，
	是由k堆合并而来的，这样一直套娃，就能还原到原始的堆数n。
	我们由此可以定义一个方程：k + (k - 1) * a == n，a是一个大于等于0的整数。
	推算一下，有：k - 1 + (k - 1) * a == n - 1 ==》 (k - 1) * (a + 1) == n - 1。
	所以对于有解的情况，一定有(n - 1) % (k - 1) == 0。
	
第二点：枚举分界点时，step应该是k - 1而不是1。
	step为1当然也是正确的，但是却进行了很多无用的计算，导致运行时间增加。
	为什么step可以是k-1呢？因为我们设计的划分是将左部分区间[i, p]合并为1堆，
	那就一定有(p - i) % (k - 1) == 0，结合最初p = i，就可以知道step应该是k-1，
	这样会涵盖所有有效的分界点p。对于其他的分界点p，左部分不能合并为1堆，那
	这样的划分并没有意义，对于计算答案也就没有帮助了。

第三点： 最大数INT_MAX,最小数INT_MIN 

感悟：本题起初的时候有几个点没过就是因为max设太小，只有0x3f,导致后面两个数据点没过。 
*/
#include<iostream>
#include<vector>
#include<algorithm>
#include<climits>
using namespace std;

const int N = 35;
int n, k;
int a[N], S[N];
int dp[N][N][N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        S[i] = S[i - 1] + a[i];
    }
    cin >> k;
    
    if ((n - 1) % (k - 1) != 0) {
        cout << -1 << endl;
        return 0;
    }
    
    for (int len = 2; len <= n; ++len) {
        for (int i = 1; i + len - 1 <= n; ++i) {
            int j = i + len - 1;
            for (int m = 2; m <= k; ++m) {
                dp[i][j][m] = INT_MAX;//初始化 
                for (int p = i; p < j; p += k - 1) {
                    dp[i][j][m] = min(dp[i][j][m], dp[i][p][1] + dp[p + 1][j][m - 1]);
                }
            }
            dp[i][j][1] = dp[i][j][k] + S[j] - S[i - 1];
        }
    }
    
    cout << dp[1][n][1] << endl;
    return 0;
}