protobuf —— 认识和安装

news2024/9/17 7:20:22

protobuf —— 认识和安装

  • 什么是序列化和反序列化
  • 有哪些常见的什么是序列化和反序列化工具
  • Protobuf安装
    • 安装依赖
    • 开始安装
  • 连接动态库
  • 一些遗留问题

我们今天来看一个序列化和反序列化的工具：protobuf。

什么是序列化和反序列化

序列化（Serialization）和反序列化（Deserialization）是计算机科学中用于处理对象状态转换的重要概念，主要涉及数据的存储和传输。

序列化（Serialization） 是将数据结构或对象的状态信息转换成可以存储或传输的格式的过程。这个过程通常涉及将复杂的对象转换成一个格式化后的字节流，该字节流可以被写入文件、通过网络发送或存储在数据库中。序列化的目的之一是为了在需要时能够将对象的状态完全恢复，即使是在不同的时间或不同的环境中。序列化不包括对象的方法，只是其数据成员（属性）。

例如，当你需要在网络上传输一个对象时，必须将其转换成可以穿越网络的数据格式（如JSON、XML或二进制流），这就是序列化过程。

反序列化（Deserialization） 则是序列化的逆过程，即将之前序列化得到的字节流或数据格式重新转换回原来的对象或数据结构。在接收端，通过反序列化，可以从接收到的数据中重新构建出与原来完全相同的对象实例，这样就可以在接收方继续使用这个对象了。

例如，当一个序列化的对象数据通过网络到达另一台计算机时，这台计算机上的程序会通过反序列化过程读取数据并重新构建出原始对象，使得程序能够处理这个对象就像它最初在发送端一样。

序列化和反序列化广泛应用于多种场景，包括但不限于：

  • 网络通信（如RPC、Web服务）
  • 数据持久化（保存对象到文件或数据库）
  • 分布式系统间的数据交换
  • 对象的深拷贝或持久化存储
  • 异步编程和进程间通信

举个不太恰当的例子：

想象你正在经营一家蛋糕店，每天需要制作各种美味的蛋糕并送到客户手中。在这个场景中，蛋糕可以类比为程序中的复杂对象，它包含了多层蛋糕体、奶油、水果等各种组成部分，就像是对象的多个属性和方法。
序列化就像是将蛋糕打包发货的过程：

  • 假设你接到一个远距离的订单，需要将一个定制的五层水果蛋糕送到客户那里。由于蛋糕不能直接邮寄，你得把它拆解成可以安全运输的部分。你把每一层蛋糕单独包装，奶油和水果也分开装好，并附上一份详细的组装说明书（这说明书可以类比为序列化时的格式规范，比如JSON或XML）。这个过程就相当于序列化，把蛋糕（对象）的状态转换成可以传输（存储）的形式。
    反序列化则是客户收到蛋糕后的组装过程：
  • 当蛋糕送达客户手中，他们根据说明书将蛋糕体、奶油和水果一一组合起来，最终还原成你店里展示的那种精美蛋糕。这个根据说明书重新构建蛋糕的过程，就相当于反序列化，即从传输格式（字节流或特定格式的数据）中恢复出原本的蛋糕（对象）。

通过这个例子，序列化就像是将蛋糕这种复杂的对象拆分成易于传输的组件并附上组装指南，而反序列化则是按照指南将这些组件重新组合成完整的蛋糕，保证在不同地点（比如厨房到客户家中）都能享受到同样的产品体验。

有哪些常见的什么是序列化和反序列化工具

序列化和反序列化是编程中常见的需求，尤其在处理数据存储、网络通信和分布式系统中。下面是一些常见的序列化和反序列化工具，它们各有特点，适用于不同的应用场景：

  1. JSON (JavaScript Object Notation):

    • 工具/库：Jackson, Gson, Moshi, Fastjson等。
    • 特点：人可读性强，易于理解，跨语言支持广泛，适合于Web服务和轻量级数据交换。

  2. XML (eXtensible Markup Language):

    • 工具/库：JAXB, DOM, SAX, StAX等。
    • 特点：结构化、自描述性强，标准成熟，但相比JSON更冗长，处理效率较低。

  3. Protocol Buffers (protobuf):

    • 工具/库：Google的protobuf库。
    • 特点：高效、紧凑的二进制格式，支持跨语言，需先定义.proto文件，适用于高性能、高负载的场景。

  4. Apache Avro:

    • 特点：提供了一套数据序列化的格式，支持动态模式，具有良好的跨语言兼容性，常用于Hadoop生态系统中。

  5. MessagePack:

    • 特点：高效的二进制格式，类似于JSON但更紧凑，支持多种语言，适用于对性能要求较高的场景。

  6. Thrift:

    • 工具/库：Apache Thrift。
    • 特点：跨语言的服务开发框架，包括序列化协议，支持多种数据类型和传输协议，适合构建分布式服务。

  7. YAML (YAML Ain't Markup Language):

    • 工具/库：SnakeYAML等。
    • 特点：易于阅读的结构化数据格式，常用于配置文件，虽然不如JSON普及但在某些领域（如Kubernetes配置）非常流行。

  8. Chronicle Wire:

    • 特点：高性能序列化框架，特别针对Java，简化了结构并采用树状结构提高性能，适用于金融、交易等高性能需求。

  9. Kryo:

    • 特点：Java库，提供了快速且高效的对象图形序列化，适用于Java对象的序列化，尤其是游戏开发和高性能计算。

  10. CBOR (Concise Binary Object Representation):

    • 特点：类似于JSON但更紧凑的二进制格式，适用于资源受限的环境或需要高效数据交换的场景。

选择哪种序列化工具取决于具体需求，如性能要求、数据交换的双方是否需要跨语言支持、是否需要高度压缩等。每种工具都有其优势和局限性，合理选择可以极大提升系统的效率和可维护性。

Protobuf安装

这里讲一下Protobuf在Linux下的安装：

首先，获取源码（git拉或者windows上下好了传给Linux也行）：

这里给出github的网址：

https://github.com/protocolbuffers/protobuf/releases?page=5

找到这个版本：
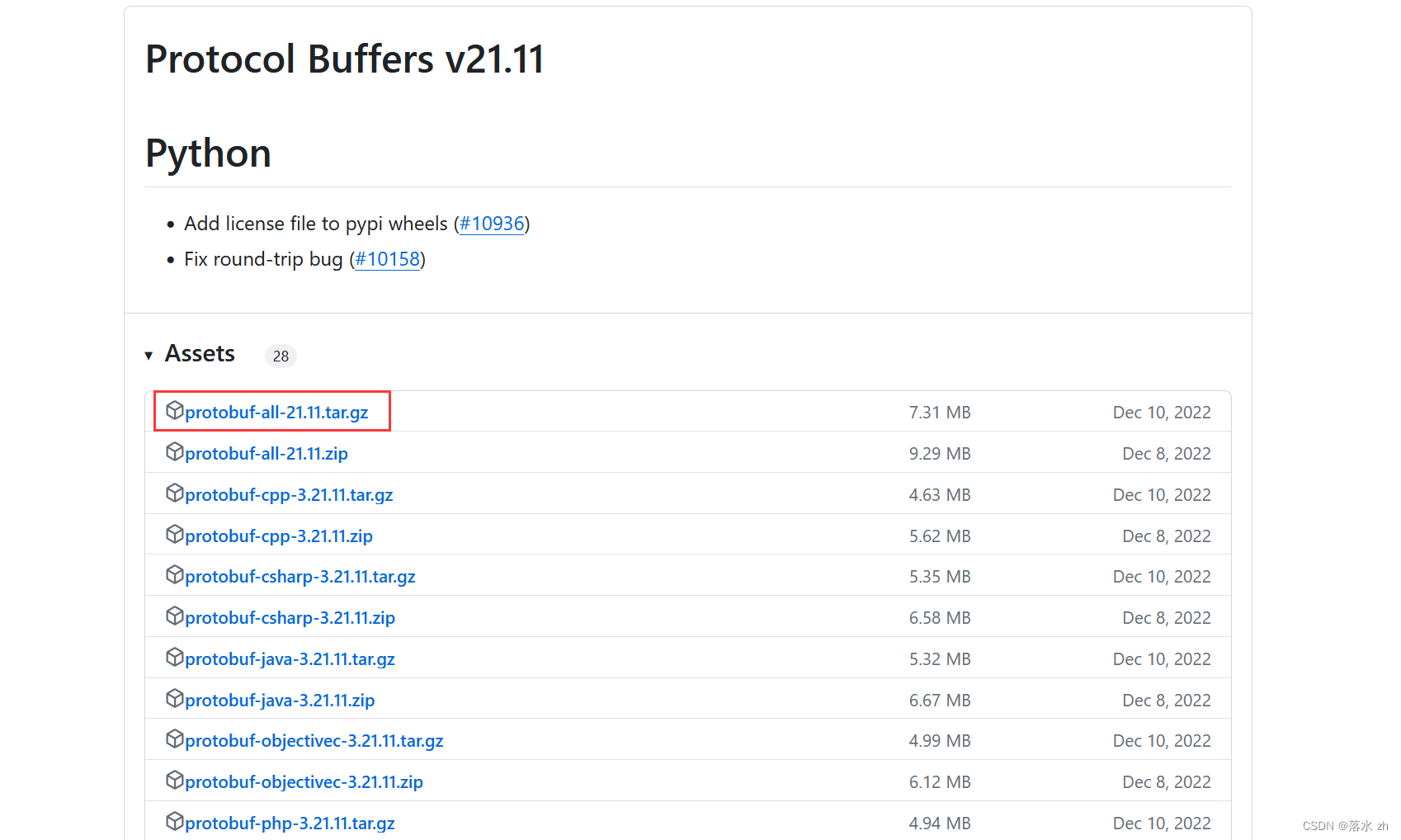
在这里插入图片描述
传到Linux上，解压：
在这里插入图片描述

安装依赖

安装之前，先安装我们需要的依赖关系：

Ubuntu 用户选择：

sudo apt-get install autoconf automake libtool curl make g++ unzip -y

CentOS 用户选择：

sudo yum install autoconf automake libtool curl make gcc-c++ unzip

如果是Centos Stream的，可以把yum换成dnf：
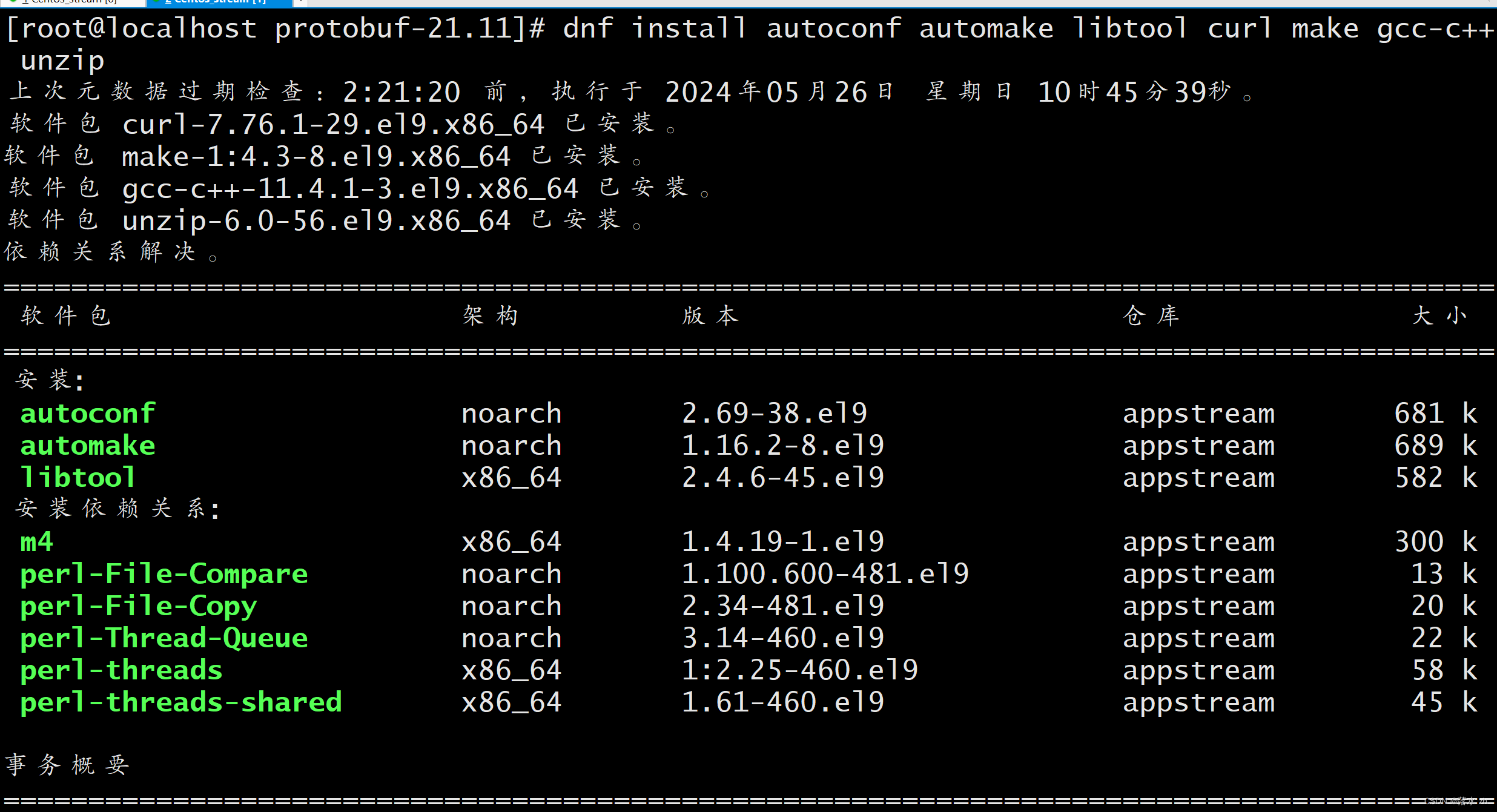
在这里插入图片描述

开始安装

第一步执行这条：

# 第⼀步执⾏autogen.sh，但如果下载的是具体的某⼀⻔语⾔，不需要执⾏这⼀步。
./autogen.sh

第二步执行：

#  第⼆步执⾏configure，有两种执⾏⽅式，任选其⼀即可，如下：

1、protobuf默认安装在 /usr/local ⽬录，
./configure

# 2、修改安装⽬录，统⼀安装在/usr/local/protobuf下
./configure --prefix=/usr/local/protobuf

第三步执行这三句：

make // 执⾏15分钟左右
make check // 执⾏15分钟左右
sudo make install

有些同学可能会在 make check 出现错误，例如：
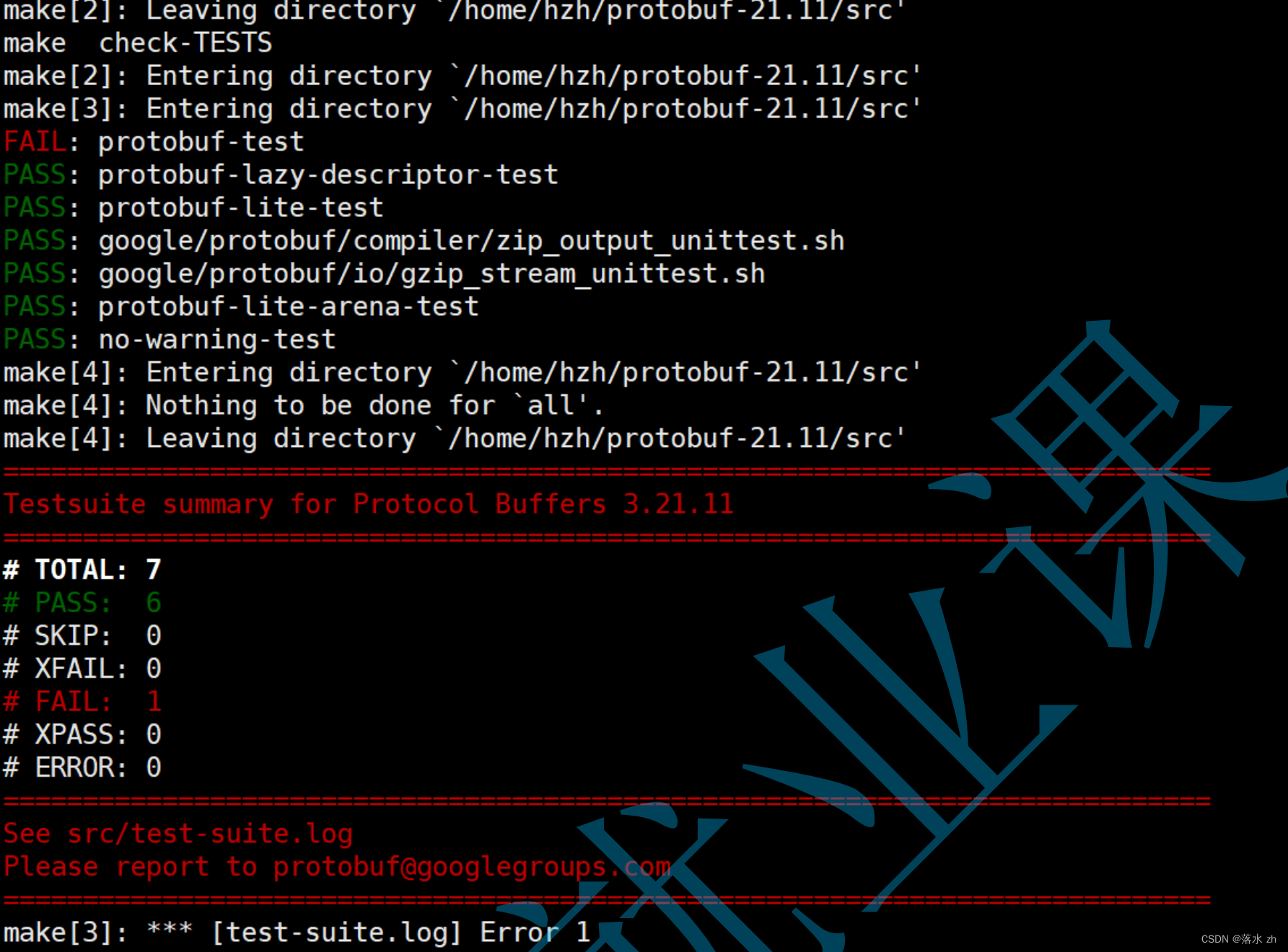在这里插入图片描述出现以上错误的原因是test的模块⾥⾯有⾮常多的测试⽤例，这些⽤例对服务器环境要求特别严格，需
要增⼤下swap分区，具体操作可参考：

https://blog.csdn.net/AlexWang30/article/details/90341172

（建议可以先扩大3G，再执行 make check 。如果还是报错，再扩⼤到5G重新执行 make check ）
执行 make check 后 ，出现以下内容就可以执行 sudo make install
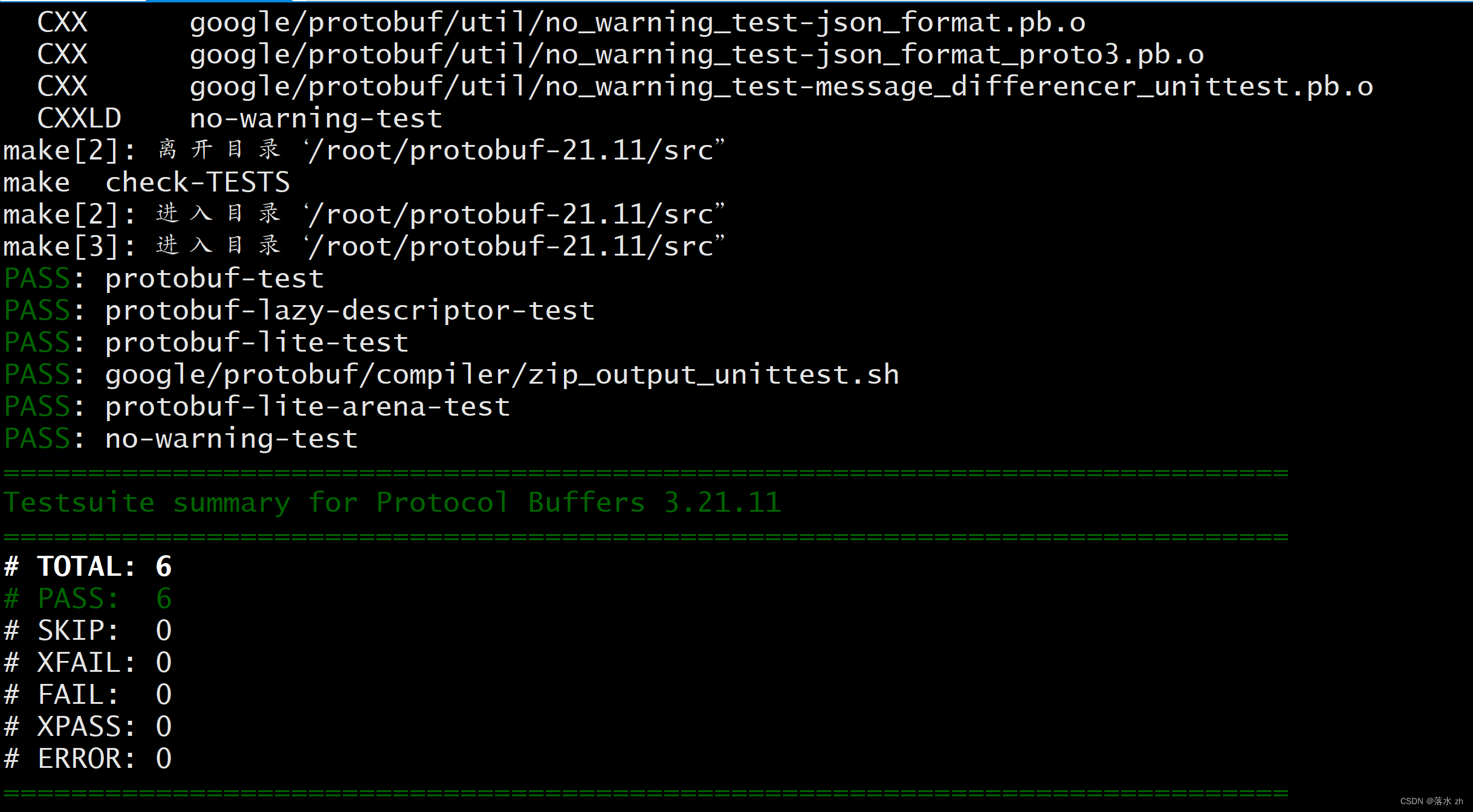在这里插入图片描述到此，需要你回忆⼀下在执行configure时，如果当时选择了第⼀种执行方式，也就是./configure ，那么到这就可以正常使⽤protobuf了。如果选择了第⼆种执行方式，即修改了安装
目录，那么还需要在/etc/profile 中添加⼀些内容：

sudo vim /etc/profile
# 添加内容如下：

#(动态库搜索路径) 程序加载运⾏期间查找动态链接库时指定除了系统默认路径之外的其他路径
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/protobuf/lib/
#(静态库搜索路径) 程序编译期间查找动态链接库时指定查找共享库的路径
export LIBRARY_PATH=$LIBRARY_PATH:/usr/local/protobuf/lib/
#执⾏程序搜索路径
export PATH=$PATH:/usr/local/protobuf/bin/
#c程序头⽂件搜索路径
export C_INCLUDE_PATH=$C_INCLUDE_PATH:/usr/local/protobuf/include/
#c++程序头⽂件搜索路径
export CPLUS_INCLUDE_PATH=$CPLUS_INCLUDE_PATH:/usr/local/protobuf/include/
#pkg-config 路径
export PKG_CONFIG_PATH=/usr/local/protobuf/lib/pkgconfig/

最后一步：

最后⼀步，重新执⾏ /etc/profile ⽂件:
source /etc/profile

在这里插入图片描述

连接动态库

此时安装好了，但可能还是不行，会报找不到动态库，
在这里插入图片描述

这个时候进入到：/etc/ld.so.conf.d/并创建一个protobuf.conf
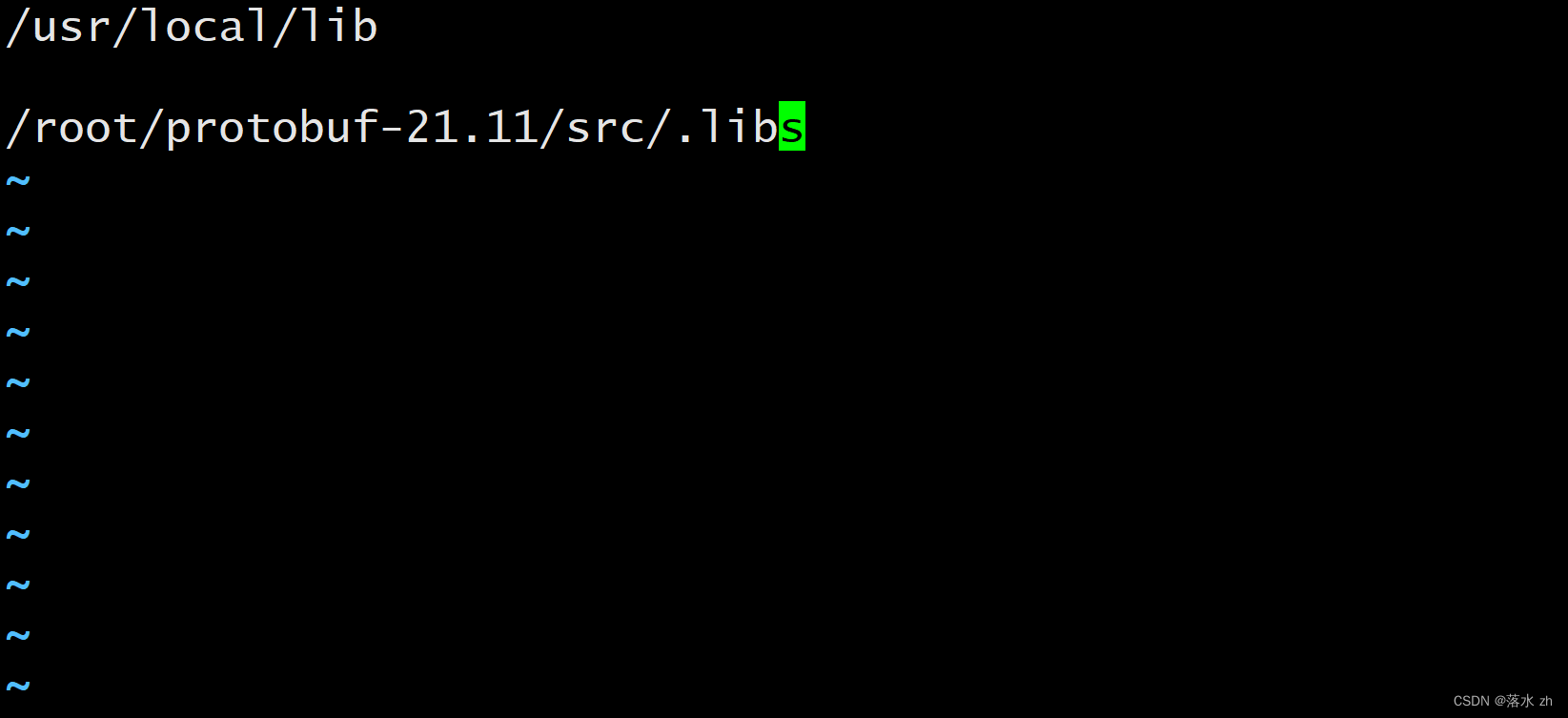在这里插入图片描述
写上这两句话：
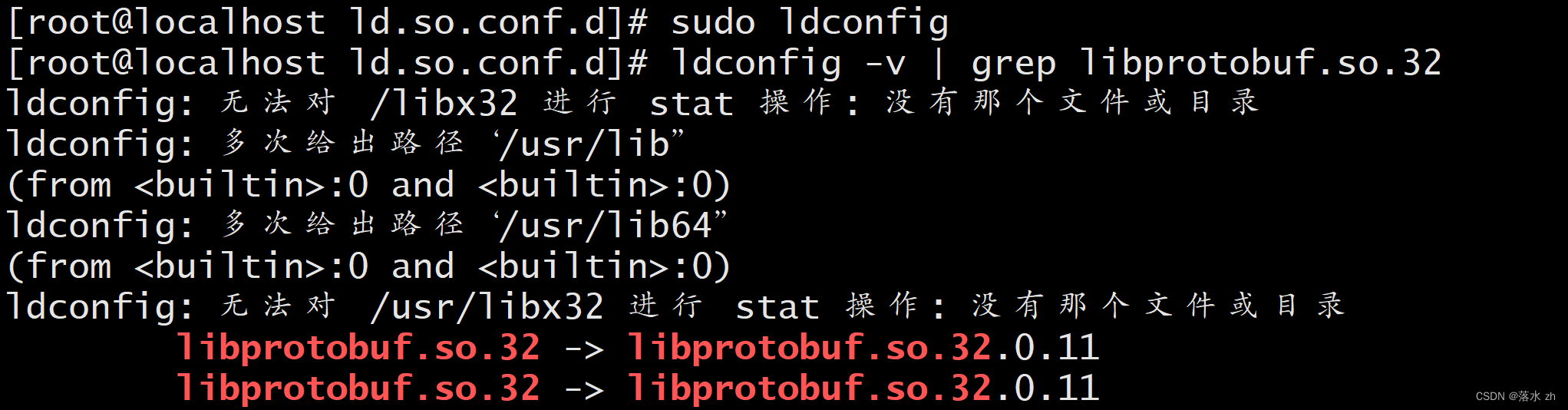
在这里插入图片描述我们再查：
在这里插入图片描述
这时候有了，这时候就不会报错了，此时真正安装成功！

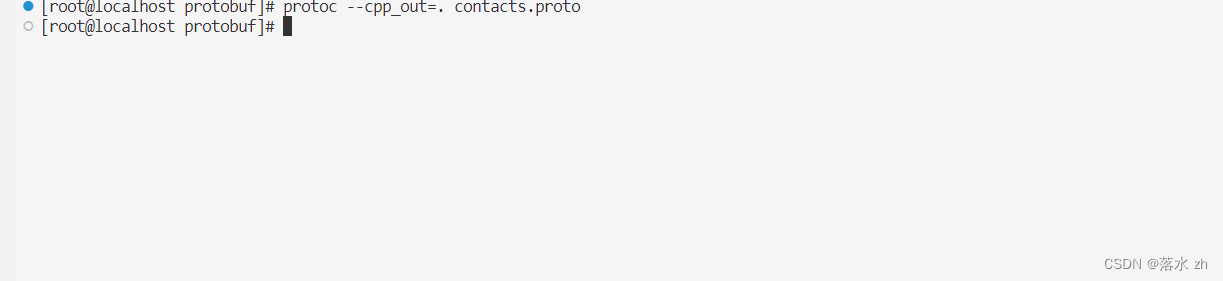
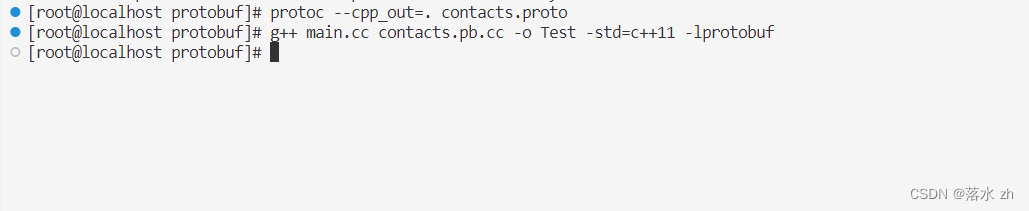
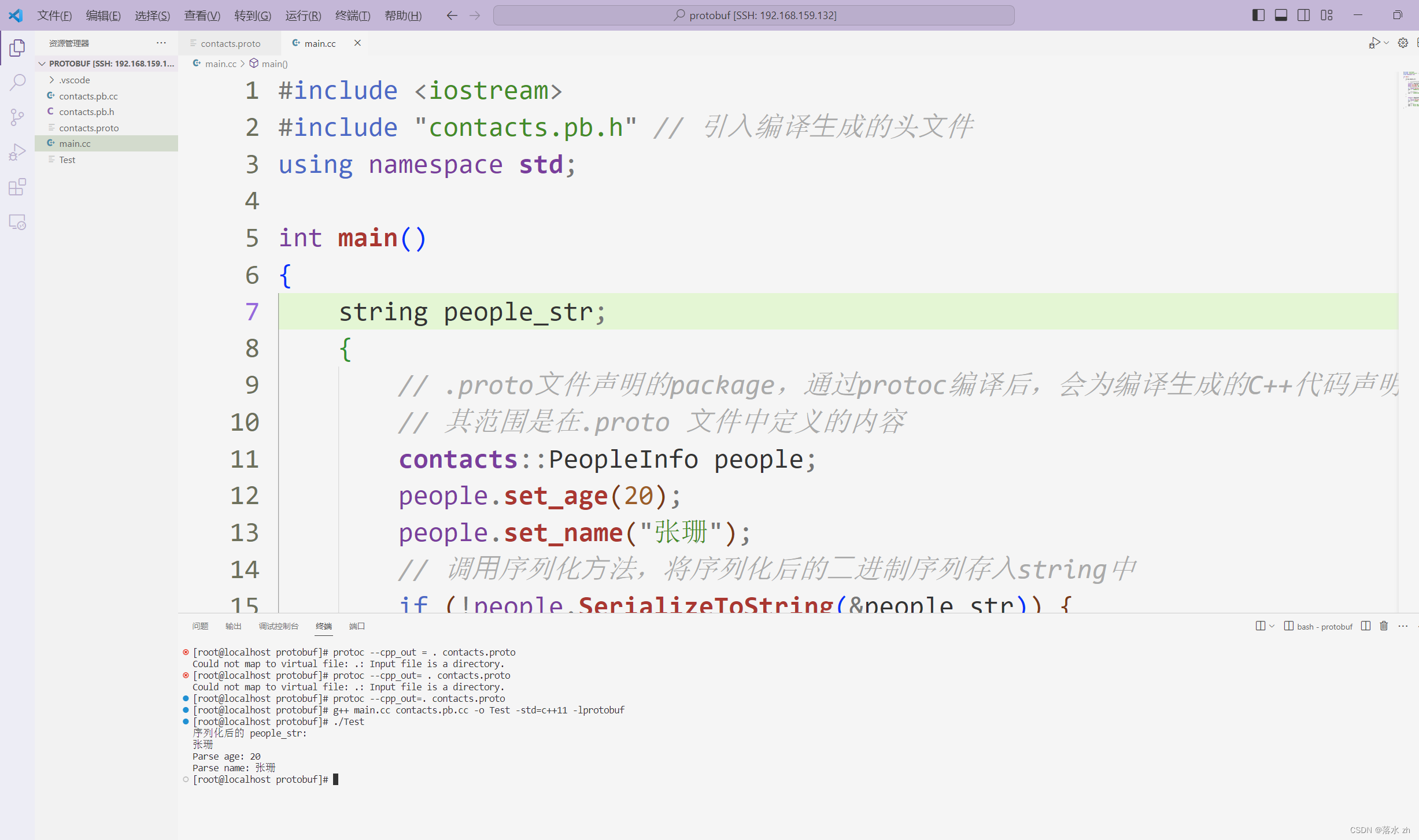
在这里插入图片描述在这里插入图片描述在这里插入图片描述

一些遗留问题

我在windows上也安装了protobuf，安装方法也比这种简单的多，但是，运行时老是报找不到port_def.inc：
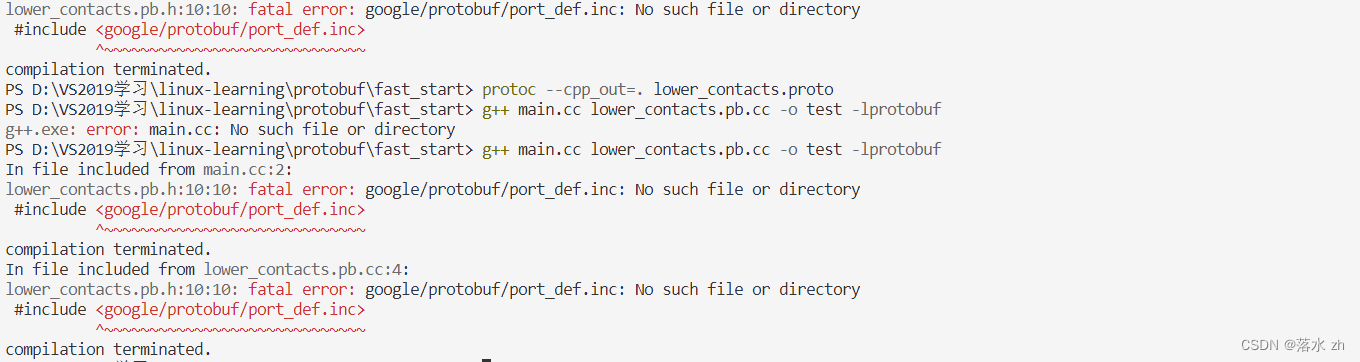
在这里插入图片描述
并且如果用cmake，nmake搭建，也会出现同样的问题，找不到port_def.inc文件，可能是我哪里有问题，肯望有大佬指点迷津！！
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1697384.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Yolov9调用COCOAPI生成APs，APm，APl

Yolov9调用COCOAPI生成APs，APm，APl

最近在做小目标检测的东西，因为后期毕业论文需要，所以开始使用Yolov9模型，运行val.py的时候不会自己产生小目标的AP指标，所以研究了一下，步骤非常简单： 第一步： 在数据集中生成json格式的Annota…
阅读更多...
【LLM多模态】综述Visual Instruction Tuning towards General-Purpose Multimodal Model

【LLM多模态】综述Visual Instruction Tuning towards General-Purpose Multimodal Model

note 文章目录 note论文1. 论文试图解决什么问题2. 这是否是一个新的问题3. 这篇文章要验证一个什么科学假设4. 有哪些相关研究？如何归类？谁是这一课题在领域内值得关注的研究员？5. 论文中提到的解决方案之关键是什么？6. 论文中的…
阅读更多...
AIGC时代算法工程师的面试秘籍（2024.4.29-5.12第十三式） |【三年面试五年模拟】

AIGC时代算法工程师的面试秘籍（2024.4.29-5.12第十三式） |【三年面试五年模拟】

写在前面 【三年面试五年模拟】旨在整理&挖掘AI算法工程师在实习/校招/社招时所需的干货知识点与面试方法，力求让读者在获得心仪offer的同时，增强技术基本面。也欢迎大家提出宝贵的优化建议，一起交流学习💪 欢迎大家关注Rocky…
阅读更多...
LVS精益价值管理系统 DownLoad.aspx 任意文件读取漏洞复现

LVS精益价值管理系统 DownLoad.aspx 任意文件读取漏洞复现

0x01 产品简介 LVS精益价值管理系统是杭州吉拉科技有限公司研发的一款专注于企业精益化管理和价值流优化的解决方案。该系统通过集成先进的数据分析工具、可视化的价值流映射技术和灵活的流程改善机制，帮助企业实现高效、低耗、高质量的生产和服务。 0x02 漏洞概述…
阅读更多...
【数据库】基于PyMySQL连接并使用数据库（代码示例）

【数据库】基于PyMySQL连接并使用数据库（代码示例）

这里写目录标题 前言1、安装PyMySQL2、打开要连接的数据库3、创建数据库连接4、获取数据库版本5、新建数据库表6、向表中插入数据7、查询表中的相关记录8、更新表中的相关记录9、删除表中的相关记录10、关闭游标和连接完整代码 前言 本文演示了如何基于PyMySQL使用代码来创建数…
阅读更多...
异步获取线程执行结果，JDK中的Future、Netty中的Future和Promise对比

异步获取线程执行结果，JDK中的Future、Netty中的Future和Promise对比

JDK中的Future和Netty中的Future、Promise的关系 三者源头追溯 Netty中的Future与JDK中的Future同名，但是是两个不同的接口。Netty中的Future继承自JDK的Future，而Promise又对Netty中的Future进行了扩展。 JDK中的Future源自JUC并发包： Net…
阅读更多...
打卡信奥刷题（19）用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解

打卡信奥刷题（19）用Scratch图形化工具信奥B3972 [语言月赛 202405] 二进制 题解

进制转换是经典的编程题，尤其是10进制转换为2进制。方法是拿给定的数，不断地除2，将余数放在对应的位置，剩下的数为对应数除2向下取整 [语言月赛 202405] 二进制 题目描述 在介绍十进制转二进制的篇目中，我们总会看到…
阅读更多...
一文读懂：http免费升级https

一文读懂：http免费升级https

背景： 随着现在全民网络安全意识的日益提升，各个网站需要实现的https数量也随之提升，那么如何将原本网站的http访问方式升级为https呢？ 该内容为如何免费将网站的http访问升级为https访问 论https的加密逻辑： 步骤 …
阅读更多...
【计算机网络】初识Tcp协议

【计算机网络】初识Tcp协议

💻文章目录 📄前言Tcp基础概念Tcp 的报文格式三次握手四次挥手 Tcp的滑动窗口机制概念超时重传机制高速重传 TCP传输控制机制流量控制拥堵控制慢启动 Tcp的性能优化机制延迟应答捎带应答 📓总结 📄前言 TCP三次握手、四次挥手&…
阅读更多...
element-ui 实现输入框下拉树组件（2024-05-23）

element-ui 实现输入框下拉树组件（2024-05-23）

用element-ui的 el-input&#xff0c;el-tree&#xff0c;el-popover组件组合封装 import url("//unpkg.com/element-ui2.15.14/lib/theme-chalk/index.css"); <script src"//unpkg.com/vue2/dist/vue.js"></script> <script src"//…
阅读更多...
SEO之核心关键词（一）

SEO之核心关键词（一）

初创企业需要建站的朋友看这篇文章&#xff0c;谢谢支持&#xff1a; 我给不会敲代码又想搭建网站的人建议新手上云 选择关键词的第一步是确定网站核心关键词。 核心关键词通常就是网站首页的目标关键词。一般来说&#xff0c;整个网站会有很多目标关键词&#xff0c;这些关键…
阅读更多...
记一次MySQL执行修改语句超时问题

记一次MySQL执行修改语句超时问题

异常问题 原因分析 这个问题发生在开发环境&#xff0c;怀疑是提交事务时终止项目运行&#xff0c;没有提交该事务&#xff0c;造成死锁 调试该事务时时间太长&#xff0c;为什么说有这个原因呢&#xff0c;因为通过查找日志显示 The client was disconnected by the server …
阅读更多...
【二叉树算法题记录】236. 二叉树的最近公共祖先

【二叉树算法题记录】236. 二叉树的最近公共祖先

题目链接 题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为&#xff1a;“对于有根树 T 的两个节点 p、q&#xff0c;最近公共祖先表示为一个节点 x&#xff0c;满足 x 是 p、q 的祖先且 x 的深度尽可能大&#xff08;一个…
阅读更多...
Day04-Maven，SpringBoot，Tomcat下载及相关配置

Day04-Maven，SpringBoot，Tomcat下载及相关配置

1. maven 2. MaVen是一款管理和构建java项目的工具 2.1 概述 mvn -v2.1 配置Maven环境&#xff08;当前工程&#xff09; 全局配置maven 3. SpringBoot 3.1 SpringBoot入门 package com.jingwei.controller;import org.springframework.web.bind.annotation.…
阅读更多...
一个和蔼可亲的Python库，用Gooey为你的程序添加GUI

一个和蔼可亲的Python库，用Gooey为你的程序添加GUI

大家好&#xff0c;你有没有遇到过这样的情况&#xff1a;你写了一个非常棒的命令行程序&#xff0c;但当你分享给朋友或同事时&#xff0c;他们却因为害怕命令行而不愿意使用&#xff1f;这时候&#xff0c;一个简洁美观的图形用户界面&#xff08;GUI&#xff09;就派上用场了…
阅读更多...
产品经理-需求分析（三）

产品经理-需求分析（三）

1. 需求分析 从业务的需要出发&#xff0c;确定业务目的和目标&#xff0c;将业务需求转为产品需求 1.1 业务需求 业务需求 业务动机 业务目标 就是最根本的动机和目标成果&#xff0c;通过这个需求解决特定的问题 1.2 产品需求 产品需求 解决方案 产品结构 产品流程…
阅读更多...
CI/CD 管道中的自动化测试：类型和阶段

CI/CD 管道中的自动化测试：类型和阶段

在上一篇文章中&#xff0c;我们讨论了敏捷团队自动化测试用例的各种用例。其中一种情况是&#xff0c;团队希望将测试与每个构建集成&#xff0c;并将持续集成作为构建过程的一部分。 在本文中&#xff0c;我们将讨论持续集成/持续交付平台中的集成测试。 让我们先从基础知识…
阅读更多...
Spring Cloud | 服务 “注册与发现“ 框架 : Eureka框架

Spring Cloud | 服务 “注册与发现“ 框架 : Eureka框架

目录&#xff1a; Eureka 的 "工作机制" :一、Eureka 的 "工作原理" ( 两大组件 ) :1.1 Eureka Server ( 服务注册中心 )1.2 Eureka Client ( 服务/服务实例&#xff0c;其存在 "两种角色" : ①服务提供者 ②服务消费者 ) :Eureka Client 的 含义…
阅读更多...
【LeetCode刷题】滑动窗口思想解决问题:长度最小的子数组、无重复字符的最长子串

【LeetCode刷题】滑动窗口思想解决问题:长度最小的子数组、无重复字符的最长子串

【LeetCode刷题】Day 7 题目1&#xff1a;209.长度最小的子数组思路分析&#xff1a;思路1&#xff1a;暴力枚举 O(N^2^)思路2&#xff1a;滑动窗口 O(N) 题目2&#xff1a;3. 无重复字符的最长子串题目分析&#xff1a;思想1&#xff1a;暴力枚举哈希表O(N^2^)思想2&#xff1…
阅读更多...
时间（空间）复杂度（结构篇）

时间（空间）复杂度（结构篇）

目录 前言&#xff1a; 一、时间复杂度 1.1 时间复杂度的定义 1.2 时间复杂度的分析 表示方法&#xff1a; 1.3 常见的时间复杂度 1.4 时间复杂度的计算以及简单的分析 冒泡排序 折半查找&#xff08;二分查找&#xff09; 斐波那契数列&#xff08;递归&#xff09…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023