目录
前言:
一、时间复杂度
1.1 时间复杂度的定义
1.2 时间复杂度的分析
表示方法:
1.3 常见的时间复杂度
1.4 时间复杂度的计算以及简单的分析
冒泡排序
折半查找(二分查找)
斐波那契数列(递归)
二、空间复杂度
2.1 空间复杂度的定义
2.2 空间复杂度的分析
2.3 常见的空间复杂度
2.4 空间复杂度的计算以及简单分析
冒泡排序
斐波那契数列(迭代)
复杂度是计算机科学中的一个基础概念,它帮助我们理解和评估算法的效率,对于算法设计和优化至关重要。算法的复杂度通常分为时间复杂度和空间复杂度两个方面。
前言:
众所周知:程序 = 算法 + 数据结构;衡量一个算法的标准就是算法效率。那么,算法效率是指算法执行的时间和所需的存储空间。在计算机科学中,算法效率通常通过时间复杂度和空间复杂度来衡量。
一、时间复杂度
1.1 时间复杂度的定义
- 时间复杂度是衡量算法执行时间随输入规模增长而变化的度量,它指示了算法的效率和性能。
- 时间复杂度通常使用大O符号(O)来表示,表示算法执行时间的上界。
- 时间复杂度描述的是算法执行时间与输入规模的增长趋势,而不是具体的执行时间。
1.2 时间复杂度的分析
表示方法:
大O 的表示法:是用于描述函数渐进行为的数学符号。
算法中的基本操作的执行次数,为算法 的时间复杂度。随着问题规模 n 的伴随某个函数f(n)变话记作:
- 一般的忽略常数项。
- 只保留最高次幂项。
注意:我们通常表示的是一个数量级,而不是具体值或某个函数。
1.3 常见的时间复杂度
- 常数时间复杂度:O(1),表示算法的执行时间不随输入规模的增长而变化,是最理想的情况。
- 对数时间复杂度:O(log n),通常出现在二分查找等分治算法中。
- 线性时间复杂度:O(n),表示算法的执行时间与输入规模成正比。
- 线性对数时间复杂度:O(n log n),通常出现在快速排序、归并排序等分治算法中。
- 平方时间复杂度:O(n^2),通常出现在嵌套循环的算法中。
- 指数时间复杂度:O(2^n),通常出现在递归算法中。
- 多项式时间复杂度:O(n^k),k可能是大于 2 的正整数,这意味着算法在大规模数据上的性能下降较快。
1.4 时间复杂度的计算以及简单的分析
通过分析算法中基本操作的执行次数,并根据输入规模的增长情况确定时间复杂度。
三种情况:
- 最好时间复杂度
- 平均时间复杂度
- 最坏时间复杂度
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}分析:冒泡排序的时间复杂度:O(N^2)
解释:有N个个数,每次移动N-1次,剩下(N-1)移动(N-2)次,总共执行(N*(N-1)/2)次,根据大O表示就是:
折半查找(二分查找)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}分析:折半查找的时间复杂度:最好是O( 1 ) ,最坏是O( log N ) ,该式表示:以2为底N的对数(仅限在计算机中表示)
解释:在查找的时候每次折半,也就是除以 2,一次是2^1,两次是 2^2,推广到N次数。
斐波那契数列(递归)
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
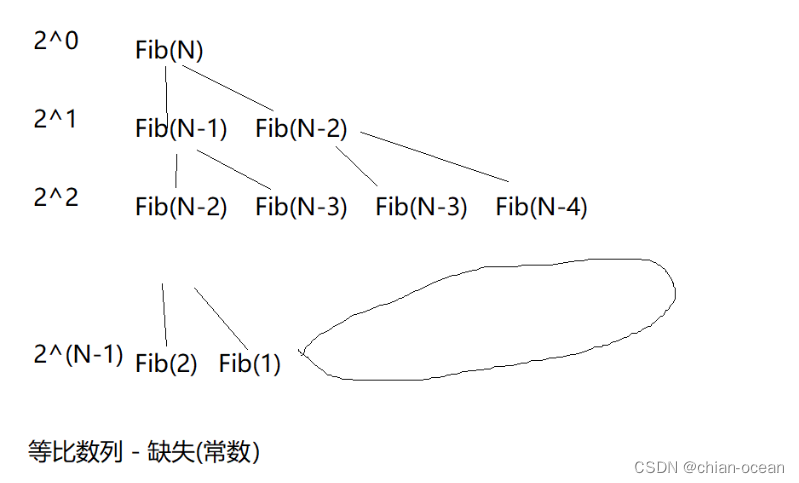
}分析:斐波那契数列时间复杂度:O(2^n)
解释:
二、空间复杂度
2.1 空间复杂度的定义
- 空间复杂度(Space Complexity)是衡量算法在执行过程中临时占用存储空间大小的量度。
- 它反映了算法所需存储空间与输入数据大小之间的关系。
- 空间复杂度通常用大O表示法来表示。
2.2 空间复杂度的分析
同时间复杂度一样用大O表示法表示;也是表示一个数量级。记作:
2.3 常见的空间复杂度
- 常数阶:如果算法的空间复杂度不随问题规模 n 的变化而变化,即算法所需的存储空间是一个常数,那么空间复杂度为 O(1)。
- 线性阶:如果算法所需的存储空间与问题规模 n 成正比,即算法所需的存储空间随着 n 的增加而线性增加,那么空间复杂度为 O(n)。
- 多项式阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为多项式函数,即空间复杂度为 O(n^k),其中 k 是一个正整数。
- 对数阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为对数函数,即空间复杂度为 O(log n)。
- 指数阶:如果算法所需的存储空间与问题规模 n 的关系可以表示为指数函数,即空间复杂度为 O(2^n)。
2.4 空间复杂度的计算以及简单分析
计算空间复杂度时,需要考虑算法在运行过程中显式申请的额外空间,而不是函数运行时所需要的栈空间,后者在编译期间已经确定好了
冒泡排序
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}分析:冒泡排序空间复杂度:O(1)
解释:仅仅使用了一个额外变量。
斐波那契数列(迭代)
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}分析:斐波那契数列空间复杂度:O( N )
解释:开辟了N个空间。