参考资料：《机器人学导论》John.J.Craig

彻底搞懂“旋转矩阵/欧拉角/四元数”，让你体会三维旋转之美_欧拉角判断动作-CSDN博客

机器人操作的定义是指通过某种机构使零件和工具在空间运动。因此，对于坐标系的定义显得尤为重要，相对于什么坐标系是描述位姿的基础。 

位姿描述，描述的是位置和姿态。比如对于一个操作臂，我们除了要知道它处于什么位置之外，它的姿态也尤为重要。自然地，我们会研究如何用数学方法去表示和计算这些参量。

为了描述位置，我们需要先固定参考系，任一坐标系都能用作描述物体位姿的参考系，我们经常在不同的参考系中变换表示物体空间位姿的形式。

1.位置描述

位置矢量，左上角标注参考系

 2.姿态描述

旋转矩阵表示姿态

3.坐标系描述-位姿 

 

4映射-坐标变换 

平移、旋转

下文中比较关键的内容

注意矩阵的行列的含义 

 注意是左乘旋转矩阵

 

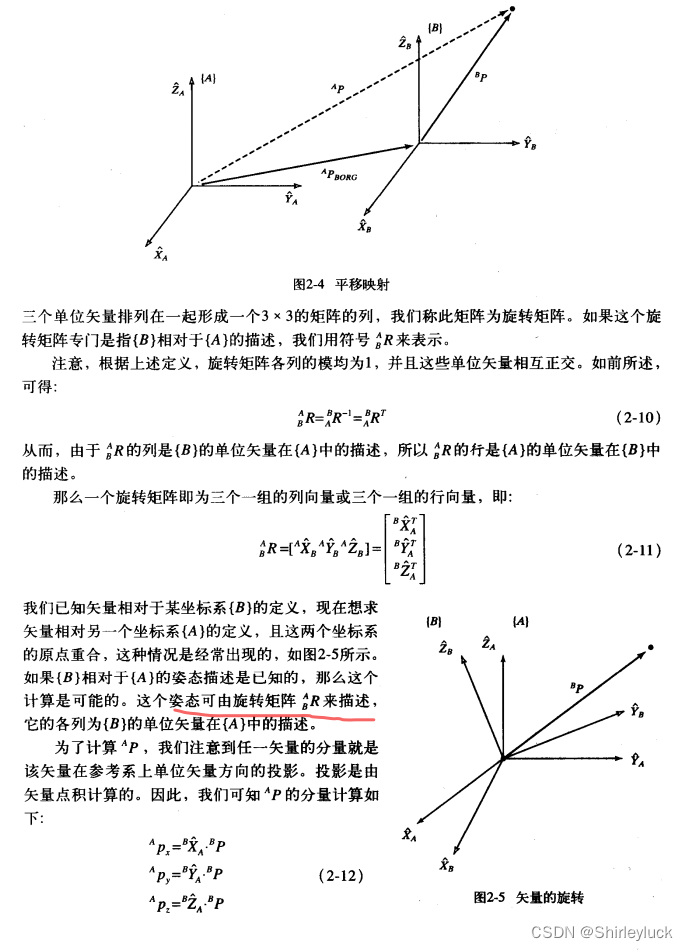
 例题：

 旋转矩阵

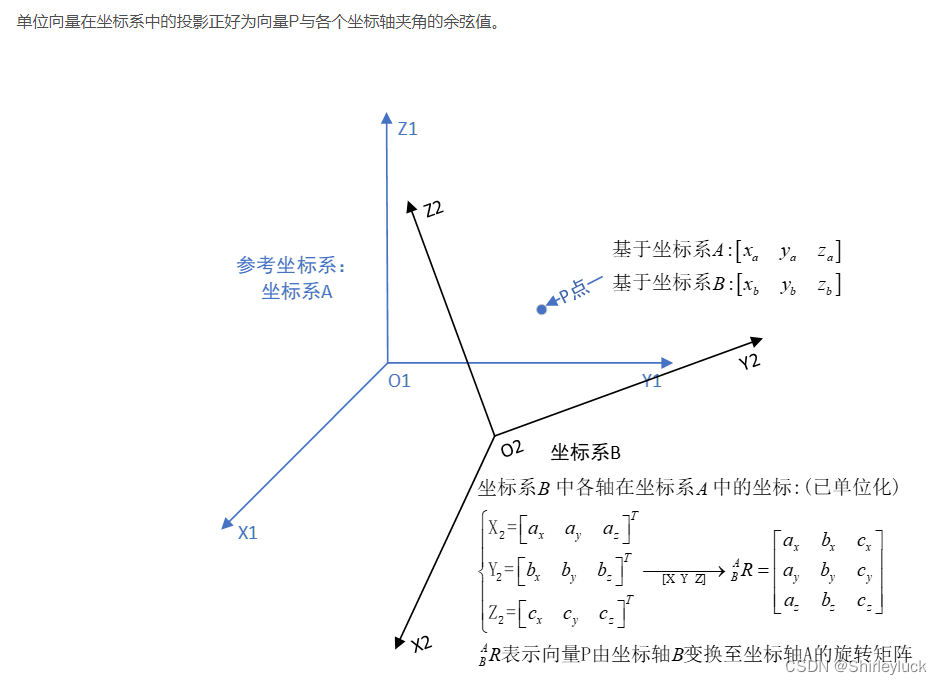
可以看到在做坐标变换的时候旋转矩阵很重要，那旋转矩阵又是怎么得到的呢？

此部分参考：彻底搞懂“旋转矩阵/欧拉角/四元数”，让你体会三维旋转之美_欧拉角判断动作-CSDN博客

（重要的好文章，虽然还不太理解四元数，先放着标记一下）

 

平移+旋转