[数据结构1.0]计数排序

news2024/9/20 22:38:01

读者老爷好，本鼠鼠最近学了计数排序，浅浅介绍一下！

1.统计相同元素出现次数

2.根据统计的结果将序列回填到原来的序列中

3.相对映射计数排序

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用，是非比较排序的一种！

这个排序算法不难理解，万物皆可举例，我们举例讲解啊！

很久很久以前，有一只可爱的肥龙猫，叫做冬冬。有一天冬冬的男朋友给冬冬出了一个题目：有一组数组a如下，要冬冬用排序算法排成升序。

聪明的冬冬使用了计数排序解决了这个问题，还将解决办法告诉了本鼠，方法如下：

1.统计相同元素出现次数

冬冬遍历数组a后知道最大的元素是9。所以冬冬开了一个大小为10*sizeof(int)的数组tmp，并将数组tmp元素全部初始化为0，如下图。用来统计相同元素出现的次数：

冬冬再次遍历数组a：遇到第一个元素是5，那么冬冬就将tmp[5]++，tmp[5]就等于1了；遇到第二个元素是3，冬冬就将tmp[3]++，tmp[3]就等于1了；遇到第三个元素是5，冬冬就将tmp[5]++，tmp[5]就等于2了；…………

冬冬说其实采用了绝对映射的办法，将a的各个元素绝对映射到tmp的元素下标当中，a的相同元素出现的次数就体现在tmp相对应下标元素的值。例如a元素5就出现了3次（a[5]==3）。

2.根据统计的结果将序列回填到原来的序列中

冬冬遍历tmp就知道了a相同元素出现的次数：a元素0出现了0次、1出现了0次……3出现了1次、4出现了0次…………

冬冬在遍历tmp的同时将a回填好就行了！

冬冬还用代码验证了可行性，本鼠偷偷将代码附上：

//绝对映射计数排序
void CountingSort(int* a, int n)
{
	int max = a[0];
	//遍历找a元素最大值
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
	}
	//动态申请a元素最大值+1个sizeof(int)数组并初始化
	int* tmp = (int*)calloc(max + 1, sizeof(int));
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//统计a相同元素出现次数
	for (int i = 0; i < n; i++)
	{
		tmp[a[i]]++;
	}
	//根据统计结果回填a
	int j = 0;
	for (int i = 0; i < max + 1; i++)
	{
		while (tmp[i]--)
		{
			a[j++] = i ;
		}
	}
}

冬冬的测试代码本鼠也偷偷拿来了：

int main()
{
	int a[] = { 5,3,5,8,5,9 };
	CountingSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

3.相对映射计数排序

冬冬是一只精益求精的肥龙猫，它想如果需排序数组a元素都在1000左右的话，如图：

用绝对映射计数排序的话，动态申请的用来统计a相同元素出现次数的tmp要开1000*sizeof(int)个字节的空间，而且大部分空间都没有用到，如图红色部分都浪费了！

a元素999映射tmp[999]的下标999、990映射tmp[990]的下标990……

冬冬就想了一个办法，采用相对映射实现计数排序。冬冬遍历数组a找到最大元素999和最小元素990，得出a的元素数据范围，动态申请数组tmp就开a的元素数据范围+1个sizeof(int)大小的空间就好了！

a元素999映射tmp[9]的下标9、990映射tmp[0]的下标0……

其实相对映射就是将a元素映射tmp对应元素下标都减去了a的最小元素值（这里是990）！

冬冬说那么回填a的时候，对应元素下标记得都加上a的最小值再回填到a就好了！

//相对映射计数排序
void CountingSort(int* a, int n)
{
	//遍历a找出最大元素和最小元素
	int max = a[0], min = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	//动态申请a元素数据范围+1个sizeof(int)字节数组并初始化
	int* tmp = (int*)calloc(max - min + 1, sizeof(int));
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//统计a相同元素出现次数
	for (int i = 0; i < n; i++)
	{
		tmp[a[i] - min]++;
	}
	//根据统计结果回填a
	int j = 0;
	for (int i = 0; i < max - min + 1; i++)
	{
		while (tmp[i]--)
		{
			a[j++] = i + min;
		}
	}
}

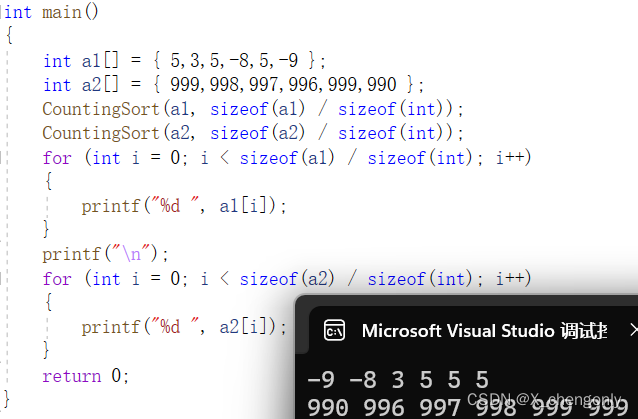
冬冬说采用相对映射对于a中有负数也一样适用，如果采用绝对映射的话就不行捏（绝对映射到的下标不可能是负数）：

int main()
{
	int a1[] = { 5,3,5,-8,5,-9 };
	int a2[] = { 999,998,997,996,999,990 };
	CountingSort(a1, sizeof(a1) / sizeof(int));
	CountingSort(a2, sizeof(a2) / sizeof(int));
	for (int i = 0; i < sizeof(a1) / sizeof(int); i++)
	{
		printf("%d ", a1[i]);
	}
	printf("\n");
	for (int i = 0; i < sizeof(a2) / sizeof(int); i++)
	{
		printf("%d ", a2[i]);
	}
	return 0;
}