---

👉博__主👈：米码收割机
👉技__能👈：C++/Python语言
👉公众号👈：测试开发自动化【获取源码+商业合作】
👉荣__誉👈：阿里云博客专家博主、51CTO技术博主
👉专__注👈：专注主流机器人、人工智能等相关领域的开发、测试技术。

---

python tkinter 计算器GUI版本（模仿windows计算器 源码）【独一无二】

---

目录

• python tkinter 计算器GUI版本（模仿windows计算器 源码）【独一无二】
• 一、功能展示
• 二、代码分析

---

一、功能展示

使用python tkinter 实现可视化计算器开发，主要模拟windows自带的科学计算器，展示如下：

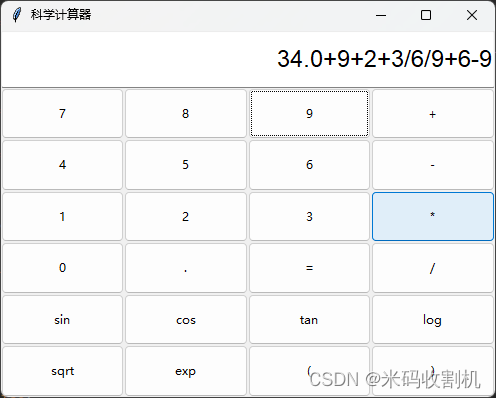
👉👉👉 源码获取 关注【测试开发自动化】公众号，回复 “计算器” 获取。👈👈👈

二、代码分析

1. 用户界面（UI）设计：

   • 标题和显示：在顶部明确的标题下开始，例如“科学计算器”。在标题下方创建一个输入框小部件，用于显示方程和结果。
   • 按钮：设计数字（0-9）、算术运算符（+、-、*、/）、特殊函数（sin、cos、tan、log、sqrt、exp）、小数点（.）、括号和等号（=）按钮。确保布局直观且易于使用。

2. 类结构：

   • CalcApp 类：表示主应用程序窗口和功能。它初始化UI并处理按钮点击。
   • 属性：
     • master：主Tkinter窗口。
     • equation：一个StringVar，用于存储当前输入或计算的方程。
     • display：输入框小部件，用于显示方程。
   • 方法：
     • __init__()：设置UI组件和布局。
     • on_click(key)：处理按钮点击。如果点击了等号按钮，则计算方程并显示结果。否则，更新正在输入的方程。

👉👉👉 源码获取 关注【测试开发自动化】公众号，回复 “计算器” 获取。👈👈👈

3. 按钮布局：

   • 定义一个元组列表，其中每个元组包含按钮的文本、其在网格布局中的行和列。
   • 通过此列表迭代，使用ttk.Button创建按钮。当点击按钮时，使用lambda函数将按钮文本传递给on_click()方法。

4. 网格布局管理：

   • 使用grid()方法将小部件（按钮和显示）放置在主窗口的行和列中。
   • 通过配置行和列权重，确保正确的对齐和调整大小行为。

5. 错误处理：

   • 为计算失败的情况（例如除以零或无效语法）实现错误处理。在输入框小部件中显示错误消息。

6. 主要功能：

   • 当点击等号按钮时，使用eval()函数评估方程。在输入框小部件中显示结果。
   • 允许用户在单个方程中输入多个操作和函数。

7. 主函数：

   • 创建主Tkinter窗口（Tk()）并实例化CalcApp类。
   • 使用mainloop()启动事件循环，以保持应用程序运行。

👉👉👉 源码获取 关注【测试开发自动化】公众号，回复 “计算器” 获取。👈👈👈