1.概述

（1）并查集支持查找一个元素所属的集合以及两个元素各自所属的集合的合并运算。当给出两个元素的一个无序对 (a, b) 时，需要快速“合并” a 和 b 分别所在的集合，这期间需要反复“查找”某元素所在的集合。“并”、”查“和”集“ 3 个字由此而来。

（2）在这种数据类型中，n 个不同的元素被分为若干组。每组是一个集合，这种集合叫分离集合，称之为并查集 (union-find disjoint set)。

2.代码实现

（1）并查集必须借助某种数据结构来实现，例如数组实现、链表实现和树实现，其中树实现使用的比较多。

（2）具体的代码实现如下：

//并查集
class UnionFind {
    //记录连通分量(树)的个数
    private int count;
    //节点 x 的根节点是 root[x]
    private int[] root;
    
    //构造函数
    public UnionFind(int n) {
        //初始时每个节点都是一个连通分量
        this.count = n;
        root = new int[n];
        //初始时每个节点的根节点都是其自己，即每棵树中只有一个节点
        for (int i = 0; i < n; i++) {
            root[i] = i;
        }
    }
    
    //将 p 和 q 连通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) {
            // p 和 q 的根节点相同，它们本就是连通的，直接返回即可
            return;
        } else {
            root[rootQ] = rootP;
            // 两个连通分量合并成一个连通分量
            count--;
        }
    }
    
    //判断 p 和 q 是否互相连通，即判断 p 和 q 是否在同一颗树中
    public boolean isConnected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        //如果 p 和 q 的根节点相同，则说明它们在同一颗树中，即它们是连通的
        return rootP == rootQ;
    }
    
    //查找节点 x 的根节点
    public int find(int x) {
        if (root[x] != x) {
            root[x] = find(root[x]);
        }
        return root[x];
    }
    
    //返回连通分量(树)的个数
    public int getCount() {
        return count;
    }
}

3.应用

（1）LeetCode 中的990.等式方程的可满足性便是对并查集的应用：

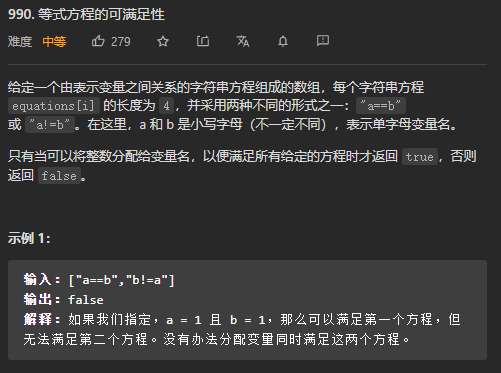
在这里插入图片描述

分析题目可知：

我们可以将方程中的单字母变量看作节点；
先将具有相等关系 (==) 的字母进行连通，然后再检查不等关系 (!=) 是否打破了相等关系的连通性；
如果打破了，则说明题目给定的方程组不可满足，直接返回 false；否则返回 true；

具体的代码实现如下所示：

class Solution {
    public boolean equationsPossible(String[] equations) {
        //将 26 个英文字母看成 26 个不同的节点
        UnionFind uf = new UnionFind(26);
        //先让 equations 的每一个字符串中相等的字母形成连通分量(即关系操作符为'==')
        for (String equation : equations) {
            if (equation.charAt(1) == '=') {
                char x = equation.charAt(0);
                char y = equation.charAt(3);
                //将字母 x 和 y 进行联通
                uf.union(x - 'a', y - 'a');
            }
        }
        //再检查不等关系(!=)是否打破了相等关系(==)的连通性
        for (String equation : equations) {
            if (equation.charAt(1) == '!') {
                char x = equation.charAt(0);
                char y = equation.charAt(3);
                //此时的 x 和 y 是不等关系，而如果它们是连通的，则说明它们又是相等的，互相矛盾
                if (uf.isConnected(x - 'a', y - 'a')) {
                    return false;
                }
            }
        }
        return true;
    }
}

class UnionFind {
	...
}