数据结构（4）线段树、延迟标记、扫描线

news2024/10/7 6:47:31

活动 - AcWing

参考-《算法竞赛进阶指南》

一、延迟标记（懒标记）

在线段树的区间查询命令中，每当遇到被查询区间[l,r]完全覆盖节点时，可以直接把节点上的答案作为备选答案返回。我们已经证明，这样操作的复杂度为O(4logn)。

但是在区间修改命令中，如果某个节点被修改区间完全覆盖，那么以该节点为根的整棵子树都要更新，如果逐一更新，时间复杂度为O（n）

试想，如果我们在一次修改指令中发现节点p代表的区间被修改区间完全覆盖，并更新了所有p子树的节点，但是在之后却没有用到这些答案，那么我们的更新就白费了。

因此，我们在执行修改指令时，如果节点被修改区间完全覆盖，我们可以直接回溯，并且在节点上加一个延迟标记，表示“该节点曾被修改，但其子节点没有被更新”。

如果在后面的操作中，如果需要从p往下递归，我们再检查p是否具有标记。如果有更新p的直接子节点，再在子节点上打上标记，然后清除p的标记。

也就是说，除了在修改指令中直接划分成的O(logn)个结点外，对任意节点的修改都延迟到“在后续操作递归进入它的父节点”时进行。这样一来，查询和修改的时间复杂度都是O（logn）级别。

例题1：一个简单的整数问题2

 本题之前用树状数组和差分结合解决过。这里再介绍线段树懒标记做法。

更新懒标记需要用到pushdown函数。（与pushup函数对应）

推导区间和的懒标记pushdown的转移方程：将懒标记加到子节点的标记上，子节点的sum加上子节点区间长度*懒标记。最后清空父节点懒标记

left.add+=root.add,right.add+=root.add;

left.sum+=(LL)(left.r-left.l+1)*root.add;right.sum+=(LL)(right.r-right.l+1)*root.add;

root.add=0;

完整代码：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N =1e5+10;
typedef long long LL;

int n,m;
int w[N];
struct Node{
    int l,r;
    LL sum,add;
}tr[4*N];

void pushup(int u)
{
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void pushdown(int u)
{
    auto &root=tr[u],&left=tr[u<<1],&right=tr[u<<1|1];
    if(root.add)
    {
        left.add+=root.add,right.add+=root.add;
        left.sum+=(LL)(left.r-left.l+1)*root.add;
        right.sum+=(LL)(right.r-right.l+1)*root.add;
        root.add=0;
    }

}

void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[l],0};
    else
    {
        tr[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

void modify(int u,int l,int r,int d)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].sum+=(LL)(tr[u].r-tr[u].l+1)*d;
        tr[u].add+=d;
    }
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,d);
        if(r>mid) modify(u<<1|1,l,r,d);
        pushup(u);
    }

}
LL query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
    pushdown(u);
    int mid=tr[u].l+tr[u].r>>1;
    LL sum=0;
    if(l<=mid) sum+=query(u<<1,l,r);
    if(r>mid) sum+=query(u<<1|1,l,r);
    return sum;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);
    char op[2];
    int l,r,d;

    while(m--)
    {
        cin>>op>>l>>r;
        if(*op=='C')
        {
            cin>>d;
            modify(1,l,r,d);
        }
        else
        {
            cout<<query(1,l,r)<<endl;
        }
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5209661/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

例题2：1277. 维护序列

 处理操作多了一个将区间内每个数乘以一个值。

懒标记处理更加复杂了，对此，我们需要两个懒标记来表示一个操作。一个mul，一个add。

对每一个操作，我们可以把之归为一类操作，即：把区间乘一个数再加一个数，或者把区间加一个数再乘一个数。显然选择抽象成把区间乘一个数再加一个数更为方便。

因为如果要把区间加一个数d，我们可以直接归类为：把区间乘1再加d。

如果把区间乘一个数d，可以归类为：把区间乘d再加0。不需要多余的转化。

因此我们的懒标记pushdown方法方程为：

void eval(Node &t, int add, int mul)
{
    t.sum = ((LL)t.sum * mul + (LL)(t.r - t.l + 1) * add) % p;
    t.mul = (LL)t.mul * mul % p;
    t.add = ((LL)t.add * mul + add) % p;
}
void pushdown(int u)
{
    eval(tr[u<<1],tr[u].add,tr[u].mul);
    eval(tr[u<<1|1],tr[u].add,tr[u].mul);
    tr[u].add=0,tr[u].mul=1;
}

大体框架不变，完整代码为：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;

const int N =1e6+10;
typedef long long LL;

int n,p,m;
int w[N];
struct Node{
    int l,r;
    LL sum,add,mul;
}tr[N*4];

void pushup(int u)
{
    tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
}

void eval(Node &t, int add, int mul)
{
    t.sum = ((LL)t.sum * mul + (LL)(t.r - t.l + 1) * add) % p;
    t.mul = (LL)t.mul * mul % p;
    t.add = ((LL)t.add * mul + add) % p;
}
void pushdown(int u)
{
    eval(tr[u<<1],tr[u].add,tr[u].mul);
    eval(tr[u<<1|1],tr[u].add,tr[u].mul);
    tr[u].add=0,tr[u].mul=1;
}
void build(int u,int l,int r)
{
    if(l==r) tr[u]={l,r,w[r],0,1};
    else
    {
        tr[u]={l,r,0,0,1};
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}
void modify(int u,int l,int r,int add,int mul)
{
    if(tr[u].l>=l&&tr[u].r<=r)  eval(tr[u],add,mul);
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,add,mul);
        if(r>mid) modify(u<<1|1,l,r,add,mul);
        pushup(u);
    }
}

int query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
    else
    {
        pushdown(u);
        int mid=tr[u].l+tr[u].r>>1;
        int sum=0;
        if(l<=mid) sum=query(u<<1,l,r);
        if(r>mid) sum=(sum+query(u<<1|1,l,r))%p;
        return sum;
    }
}

int main()
{
    cin>>n>>p;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);
    cin>>m;
    while(m--)
    {
        int t,l,r,d;
        cin>>t>>l>>r;
        if(t==1)
        {
            cin>>d;
            modify(1,l,r,0,d);
        }
        else if(t==2)
        {
            cin>>d;
            modify(1,l,r,d,1);
        }
        else cout<<query(1,l,r)<<endl;
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5260636/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二、线段树+扫描线+二分查找+离散化

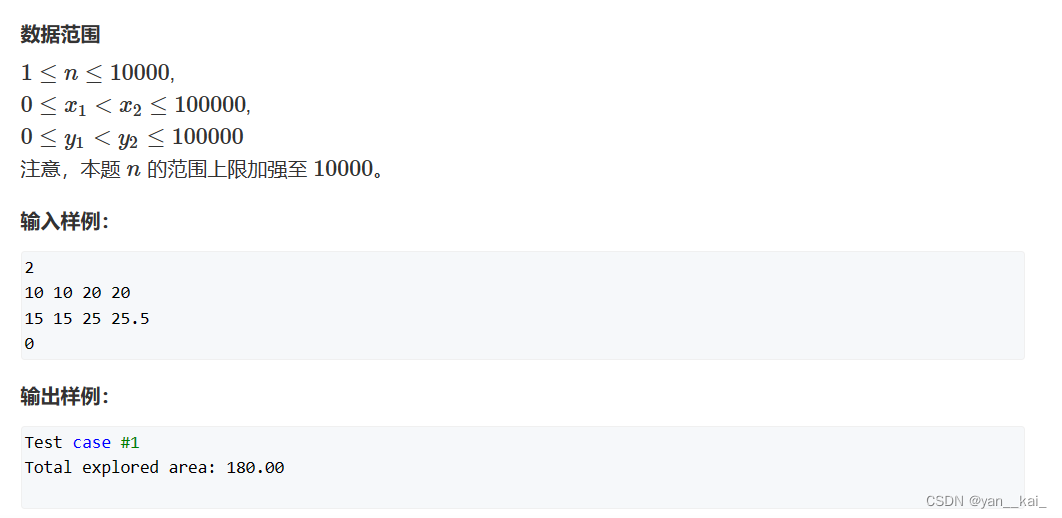
 【hdu1542】线段树求矩形面积并 - 拦路雨偏似雪花 - 博客园 (cnblogs.com)

 本人理解不到位，以后在补owo

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#include<cstdio>
#include<vector>

const int N =1e5+10;

int n;
struct Segment{
    double x,y1,y2;
    int k;
    bool operator <(const Segment &t)const
    {
        return x<t.x;
    }
}seg[2*N];

struct Node{
    int l,r;
    int cnt;
    double len;
}tr[4*2*N];

vector<double> ys;

int find(double y)
{
    // 需要返回vector 中第一个 >= y 的数的下标
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

void pushup(int u)
{
    if(tr[u].cnt)   tr[u].len=ys[tr[u].r+1]-ys[tr[u].l];
    else if(tr[u].l!=tr[u].r)
    {
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    }
    else tr[u].len = 0;//表示为叶子节点且该线段没被覆盖，为无用线段，长度变为0
}

void modify(int u,int l,int r,int d)
{
    if(tr[u].l >= l && tr[u].r <= r)//该区间被完全覆盖
    {
        tr[u].cnt += d;//该区间出现次数 + d
        pushup(u);//更新该节点的len
    }
    else
    {
        int mid = tr[u].r + tr[u].l >> 1;
        if (l <= mid)modify(u << 1,l,r,d);//左边存在点
        if (r > mid)modify(u << 1 | 1,l,r,d);//右边存在点
        pushup(u);//进行更新
    }
}
void build(int u,int l,int r)
{
    tr[u] = {l,r,0,0};

    if (l != r)
    {
        int mid = l + r >> 1;
        build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
        //后面都为0，不需更新len
    }
}

int main()
{
    int T=1;
    while(scanf("%d",&n),n)
    {
        ys.clear();
        for(int i=0,j=0;i<n;i++)
        {
            double x1,y1,x2,y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            seg[j ++ ] = {x1, y1, y2, 1};
            seg[j ++ ] = {x2, y1, y2, -1};
            ys.push_back(y1), ys.push_back(y2);   
        }
        sort(ys.begin(),ys.end());
        ys.erase(unique(ys.begin(),ys.end()),ys.end());
        build(1,0,ys.size()-2);
        sort(seg,seg+2*n);
        double res=0;
        for(int i=0;i<n*2;i++)
        {
            if(i>0) res+=tr[1].len*(seg[i].x-seg[i-1].x);
            modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
        }

        printf("Test case #%d\n", T ++ );
        printf("Total explored area: %.2lf\n\n", res);

    }
    return 0;

}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5257208/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/169541.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

01-React（脚手架+MVC/MVVM+JSX）

01-React（脚手架+MVC/MVVM+JSX）

使用 create-react-app 构建React工程化项目 安装 create-react-app $ npm i create-react-app -g 「mac需要加sudo」 基于脚手架创建项目「项目名称需要符合npm包规范」 $ create-react-app xxx 目录结构&#xff1a; |- node_modules 包含安装的模块 |- public 页面模板…
阅读更多...
79.循环神经网络的从零开始实现

79.循环神经网络的从零开始实现

从头开始基于循环神经网络实现字符级语言模型。 这样的模型将在H.G.Wells的时光机器数据集上训练。 和之前一样&#xff0c; 我们先读取数据集。 %matplotlib inline import math import torch from torch import nn from torch.nn import functional as F from d2l import to…
阅读更多...
Rockchip开发系列 - 9.watchdog看门狗

Rockchip开发系列 - 9.watchdog看门狗

By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅！ 你的喜欢就是我写作的动力！ 目录 dts中的watchdog节点watchdog驱动文件TRM watchdog：WDT框图功能描述计数器中断系统复位复位脉冲长度操作流程图寄存器描述寄存器设置…
阅读更多...
Nessus Host Discovery

Nessus Host Discovery

系列文章 Nessus介绍与安装 Nessus Host Discovery 1.启动nessus cd nessus sh qd_nessus.sh2.进入nessus网站 https://192.168.3.47:8834/3.点击【New Scan】 4.选择【Host Discovery】 5.输入name【主机发现】&#xff0c;Description【主机发现】&#xff0c;Targets【…
阅读更多...
Android 蓝牙开发——服务启动流程（二）

Android 蓝牙开发——服务启动流程（二）

首先我们要知道&#xff0c;主要系统服务都是在 SystemServer 启动的&#xff0c;蓝牙也是如此&#xff1a; 1、SystemServer 源码路径&#xff1a;/frameworks/base/services/java/com/android/server/SystemServer.java private void startOtherServices(NonNull TimingsT…
阅读更多...
labelme（2）json文件转类别灰度图

labelme（2）json文件转类别灰度图

首先感谢大佬&#xff1a;https://blog.csdn.net/tzwsg/article/details/114653071一、上代码&#xff0c;json2gray.py&#xff1a;#!/usr/bin/python # -*- coding: UTF-8 -*- # !H:\Anaconda3\envs\new_labelme\python.exe import argparse import json import os import os…
阅读更多...
go语言中变量和常量的注意点

go语言中变量和常量的注意点

1、类型转换&#xff1a;大类型可以转换成小类型但是精度丢失&#xff1b;小类型不能转换成大类型。例如&#xff1a; package mainimport "fmt"//golang中使用" var "关键字来定义变量 //定义变量的语法&#xff1a;1、var var_name1[,var_name2,...] va…
阅读更多...
day16|654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树

day16|654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树

654.最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点&#xff0c;其值为 nums 中的最大值。递归地在最大值 左边 的 子数组前缀上 构建左子树。递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums 构…
阅读更多...
深度学习入门基础CNN系列——填充（padding）与步幅（stride）

深度学习入门基础CNN系列——填充（padding）与步幅（stride）

填充&#xff08;padding&#xff09; 在上图中&#xff0c;输入图片尺寸为333\times333&#xff0c;输出图片尺寸为222\times222&#xff0c;经过一次卷积之后&#xff0c;图片尺寸为222\times222&#xff0c;经过一次卷积之后&#xff0c;图片尺寸变小。卷积输出特征图的尺寸…
阅读更多...
el-table表头添加勾选框

el-table表头添加勾选框

el-table表头添加勾选框嘚吧嘚实现嘚吧嘚 table的行勾选是比较常规的操作&#xff0c;但是有的时候就有各种奇葩的需求蹦出来。&#x1f62d; 比如最近有一个需求&#xff0c;不仅需要勾选行&#xff0c;还需要勾选列&#xff0c;其实我心中有了一万头可爱的小羊驼&#xff0c…
阅读更多...
NISP三级证书含金量如何

NISP三级证书含金量如何

国家信息安全水平测试&#xff08;NationalInformationSecurityTestProgram&#xff0c;通称NISP&#xff09;&#xff0c;是通过中国信息安全测评中心执行塑造我国网络空间安全优秀人才的一个项目。 为培养大量出色的实践型网络安全人才&#xff0c;中国信息安全测评中心上线…
阅读更多...
SpringCloud Alibaba微服务 -- Seata的原理和使用

SpringCloud Alibaba微服务 -- Seata的原理和使用

文章目录一、认识Seata1.1 Seata 是什么?1.2 了解AT、TCC、SAGA事务模式?AT 模式前提整体机制如何实现写隔离如何实现读隔离TCC 模式Saga 模式Saga 模式适用场景Saga 模式优势Saga 模式缺点二、Seata安装2.1 下载2.2 创建所需数据表2.2.1 创建 分支表、全局表、锁表2.2.2 创建…
阅读更多...
Qt OpenGL（10）光照模型基础

Qt OpenGL（10）光照模型基础

文章目录物体的光照模型立方体坐标构建立方体的6个面代码框架widget.cpp顶点着色器片元着色器Ambient 环境光Diffuse 漫反色法向量计算漫反射分量Specular Highlight镜面高光计算镜面反射分量补充&#xff1a;半程向量的使用物体的光照模型 出于性能的原因&#xff0c;一般使用…
阅读更多...
思科Cisco交换机的基本命令

思科Cisco交换机的基本命令

一、设备的工作模式1、用户模式Switch>可以查看交换机的基本简单信息&#xff0c;且不能做任何修改配置&#xff01;2、特权模式Switch> enable Switch#可以查看所有配置&#xff0c;且不能修改配置&#xff01;3、全局配置模式switch# configure terminal switch(config…
阅读更多...
Redis基础——SpringDataRedis快速入门

Redis基础——SpringDataRedis快速入门

文章目录1. SpringDataRedis介绍2. SpringDataRedis快速入门2.1 SpringDataRedis的使用步骤1. SpringDataRedis介绍 SpringData是Spring中数据操作的模块&#xff0c;包含对各种数据库的集成&#xff0c;其中对Redis的集成模块就叫做SpringDataRedis 官方网址 提供了对不同Redi…
阅读更多...
参加猿代码超算实习生计划靠谱吗？

参加猿代码超算实习生计划靠谱吗？

猿代码近期推出了超级实习生计划&#xff0c;相比市面上同类型实习类产品&#xff0c;超算实习生计划服务群体范围更小一些&#xff0c;主要服务于有志于从事芯片行业的大学生们&#xff0c;专做芯片赛道实习就业产品。那么至今为止有人参加过猿代码超算实习生计划吗?这个产品…
阅读更多...
〖产品思维训练白宝书 - 核心竞争力篇①〗- 产品经理 的核心竞争力解读

〖产品思维训练白宝书 - 核心竞争力篇①〗- 产品经理 的核心竞争力解读

大家好&#xff0c;我是 哈士奇 &#xff0c;一位工作了十年的"技术混子"&#xff0c; 致力于为开发者赋能的UP主, 目前正在运营着 TFS_CLUB社区。 &#x1f4ac; 人生格言&#xff1a;优于别人,并不高贵,真正的高贵应该是优于过去的自己。&#x1f4ac; &#x1f4e…
阅读更多...
Top 命令中的 Irix 模式与 Solaris 模式(解释单个进程cpu占比为何会超过100%？)

Top 命令中的 Irix 模式与 Solaris 模式(解释单个进程cpu占比为何会超过100%？)

文章目录 背景top cpu 栏位说明Solaris 模式Irix ModeTOP -H切换线程总结背景 关于top命令用了很久了，但是一直对单进程占用cpu占比为何会超过100%认识不够深刻。 top cpu 栏位说明 1. %CPU -- CPU UsageThe tasks share of the elapsed CPU time since the last screen…
阅读更多...
深度学习入门基础CNN系列——卷积计算

深度学习入门基础CNN系列——卷积计算

卷积计算 卷积是数学分析中的一种积分变换的方法&#xff0c;在图像处理中采用的是卷积的离散形式。这里需要说明的是&#xff0c;在卷积神经网络中&#xff0c;卷积层的实现方式实际上是数学中定义的互相关 &#xff08;cross-correlation&#xff09;运算&#xff0c;与数学…
阅读更多...
【项目实战】package.json你需要了解内容

【项目实战】package.json你需要了解内容

package.json文件^和~区别 在项目开发中常引用npm包&#xff0c;那么package.json文件^和~区别是什么&#xff1f; ^意思是将当前库的版本更新到第一个数字&#xff0c; 例&#xff1a;"^4.1.0"是库会更新到4.X.X的最新版本&#xff0c;但不会更新到5.X.X版本。~意…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023