来源:投稿 作者:愤怒的可乐
编辑:学姐
不懂数学是学不好人工智能的,本系列文章就汇总了人工智能所需的数学知识。本文是高等数学篇。 另有线代篇和概率论篇
函数与极限
函数
y=f(x) ,x是函数f的自变量,y是因变量
函数极限

-
第一种表示|x|是无穷大的,同样也可能是正数或负数;
-
第二种表示趋向于正无穷大;
-
第三种表示趋向于负无穷大;
函数极限的定义:
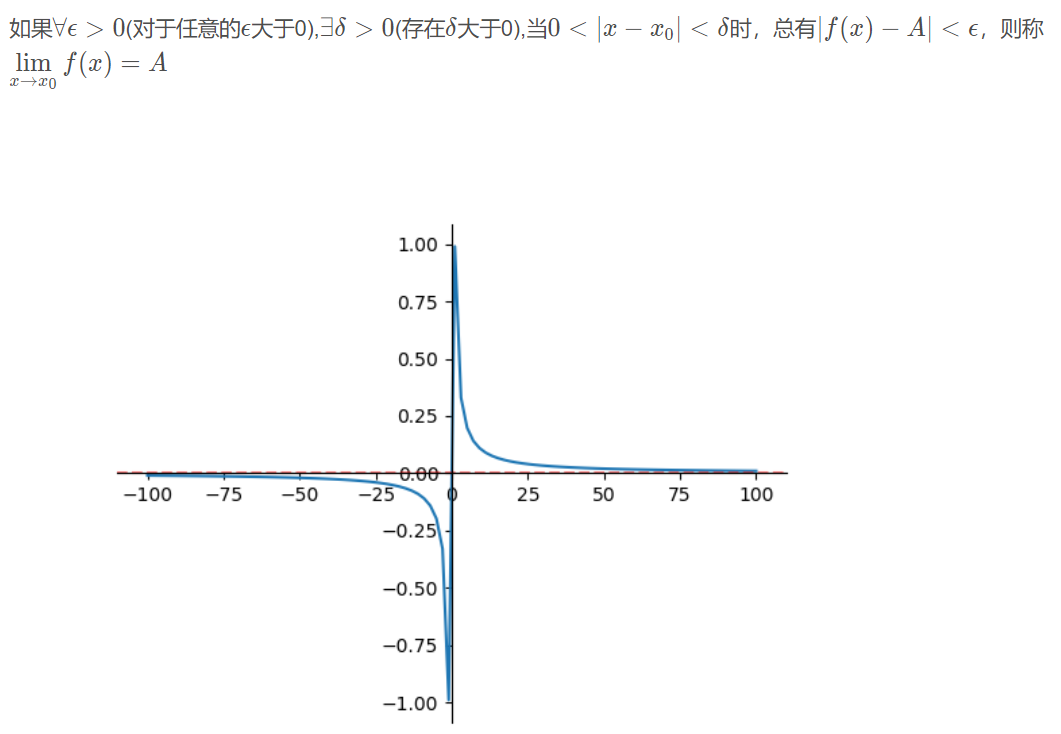
我们可以通过图形来理解极限,如上图,该函数的极限为0(x→−∞和x →+∞ ,都趋向于0,因此说x→∞时极限为0 )
该图形对应的代码为:
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
x = np.linspace(-100, 100, 100)
y = 1/x
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
# remove the ticks from the top and right edges
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
plt.axhline(0,color = 'red',linestyle = '--',alpha = 0.5)
plt.show()
无穷小与无穷大
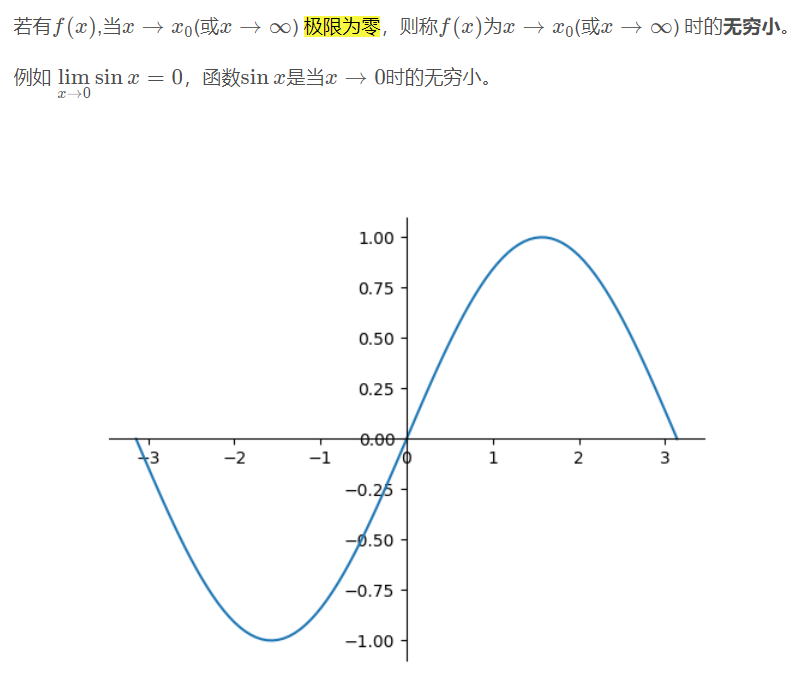
无穷小
极限为零的变量称为无穷小。
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
x = np.linspace(-np.pi, np.pi, 100)
y = np.sin(x)
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
# remove the ticks from the top and right edges
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
#plt.axhline(0,color = 'red',linestyle = '--',alpha = 0.5)
plt.show()
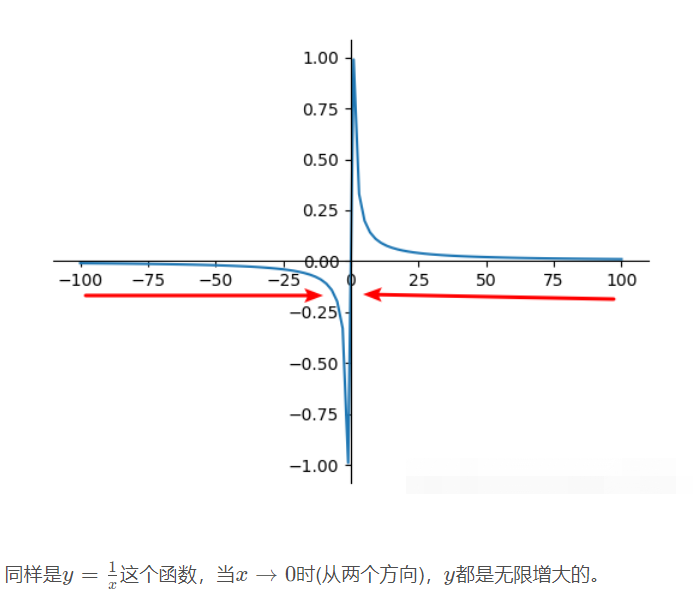
无穷大

无穷大和无穷小都是有条件的,即趋于某一点或无穷大时。
极限的四则运算
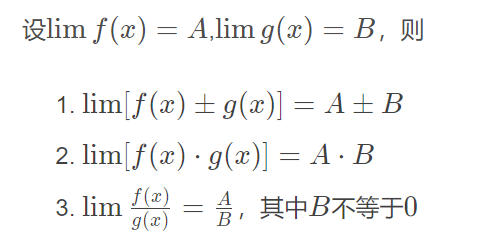
-
两个无穷小的和是无穷小
-
有界函数和无穷小的乘积是无穷小
常见函数的极限

函数连续
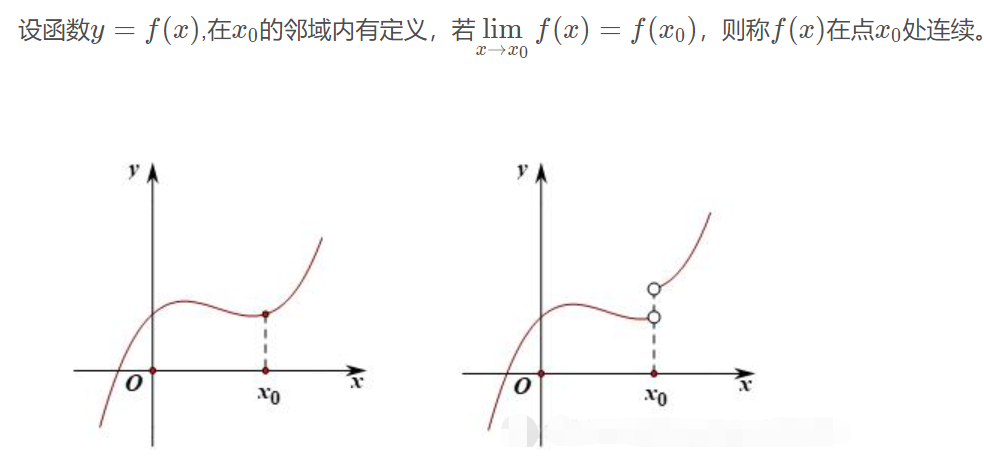
上图左边的函数是连续的,而右边的函数不是连续的。
举例

因此极限不存在,该函数在0处不连续。
连续函数的和差积商也是连续的;连续函数的符合函数是连续的;基本初等函数在其定义域内都连续。
导数
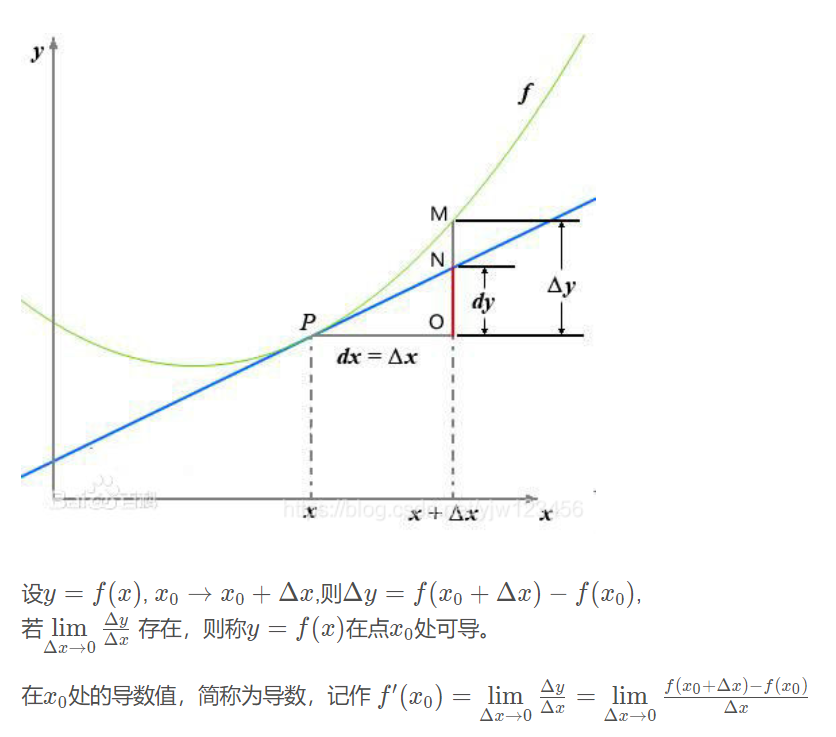
导数的理解:
-
指的是该点的变化率,可能是变大(导数为正),也可能变小(导数为负)
-
从几何意义上,是该点切线的斜率
怎么理解导数是变化率:
-
就是如果自变量x继续增加,因变量y的变化。
-
如果导数大于0,则y变大;如果导数小于0,则y变小。
-
自变量x沿着导数地方向变化,就是沿着因变量y增加的方向变化。
可导和连续
先来看一下连续和可导的几何意义


连续几何上看就是函数的图形不间断;可导的几何意义是曲线在该点处有斜率且斜率存在。
那么可导和连续的关系,我们可以通过一个图形来理解:
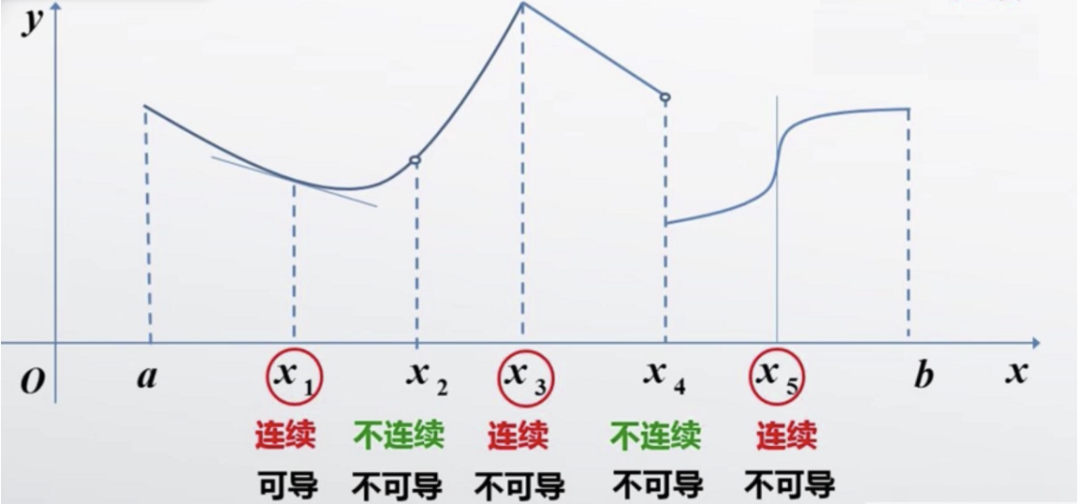
由于在X2和X4处是断开的,不连续,无法做出切线,就没有切线的斜率一说了,因此不可导。
在X3处是连续的,但是图形在X3处不光滑,没有办法做出唯一的切线,因此该点是不可导的。
X5处斜率不存在,不可导。
光滑函数:曲线不尖锐,必光滑。连续光滑的曲线,必然处处有切线,这点是必然的,没有切线(或没有唯一的切线)的地方,就不光滑。
由上可知,不连续一定不可导;可导则必然连续;连续不一定可导。
最后以一个图片作为总结:

导数的四则运算

复合函数求导法

高阶导数

二阶及二阶以上的导数称为高阶导数。
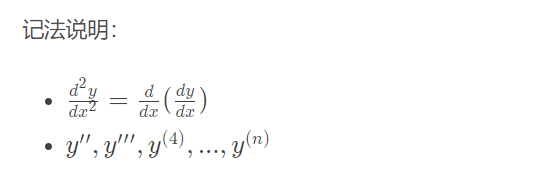
偏导数
要学习偏导数,先要了解二元函数的概念
二元函数

偏导数的概念

对y的偏导数同理。
要注意的是, 函数在一点处偏导存在,则函数在这点不一定连续。
偏导数的几何意义
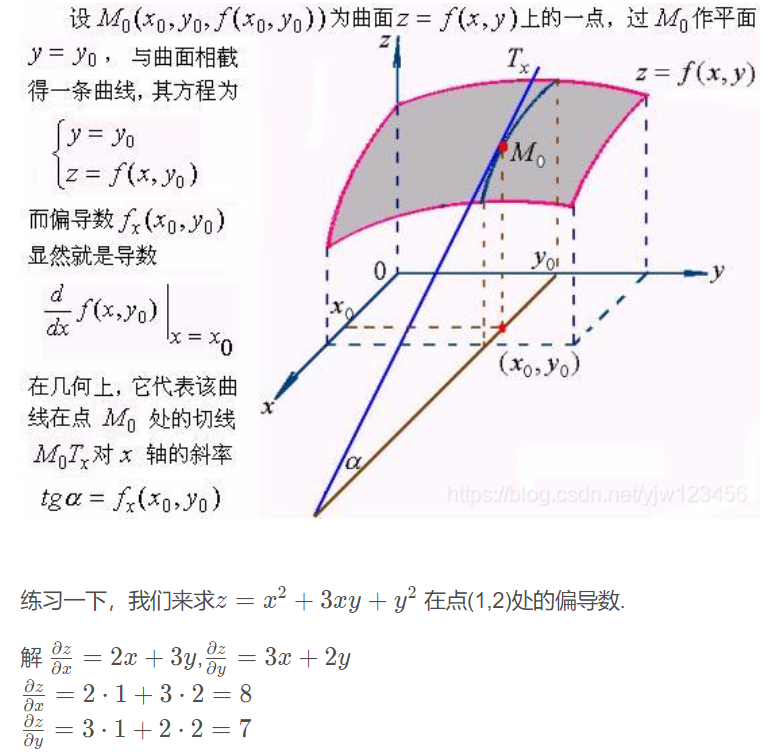
注意,求偏导的时候,把其他因变量看成常量
微分
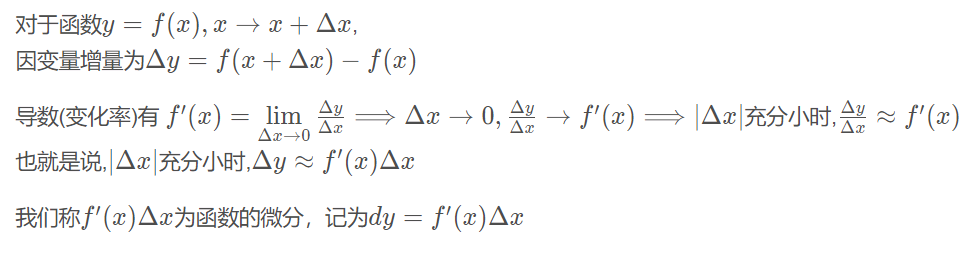
微分的意义是因变量增量的近似值(函数变化的程度)

导数从微分的角度看可以表示成因变量的微分比上自变量的微分,所以导数还有个别名叫微商。
由此也可以看出可微和可导是等价的,因此求微分时可以先求导数,再改写为微分。
中值定理
罗尔定理
如果函数y=f(x)满足条件
在[a,b]上连续;
在(a,b)内可导;
f ( a ) = f ( b );
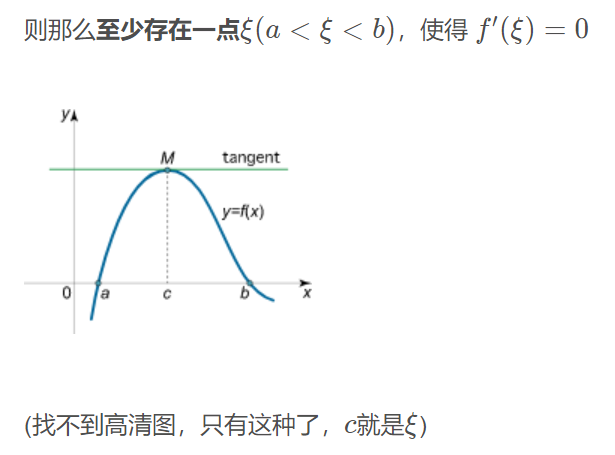
几何意义:如果连续曲线除端点外处处具有不垂直于x轴的切线,且两个端点处的纵坐标相等,那么其上至少有一点处的切线平行于x轴。
其应用是判断方程根的存在性。
拉格朗日中值定理
该定理反反映了可导函数在闭区间上整体的平均变化率与区间内某点的局部变化率的关系。

从这个函数图形来看,是不是很像罗尔定理的图形旋转了一下。并且可以看出,c点处的切线虽然不再平行于x轴,但是平行于AB两点的连线。即它们的斜率是相等的,有:
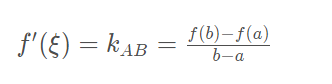
得到拉格朗日中值定理:
如果函数y=f(x)满足条件
-
在[a,b]上连续;
-
在(a,b)内可导;

几何意义:如果连续曲线除端点外处处具有不垂直于ox轴的切线,那么其上至少有这样一点存在,在该点处曲线的切线平行于连接两端点的直线,即两者斜率相同。
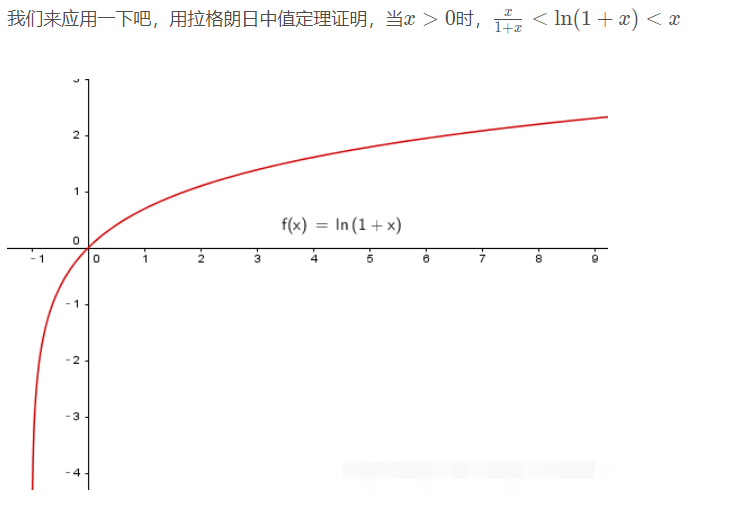

柯西中值定理
是拉格朗日中值定理的推广。
在拉格朗日中值定理中,若函数由参数方程:
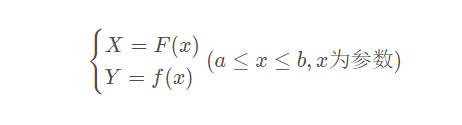
表示,如图所示
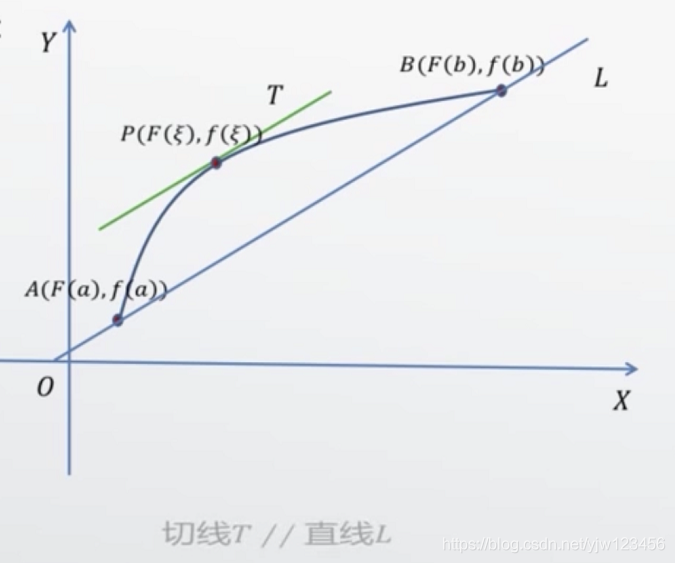
则连接两个端点A,B的直线斜率为
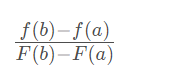
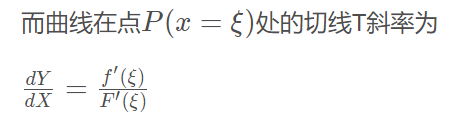
则由曲线在点P的切线T与直线L平行可知:
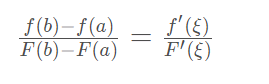
得到柯西中值定理:
如果函数f(x)和F(x)满足
-
在[a,b]上连续;
-
在(a,b)内可导,且F′( x )≠0;

洛必达法则
设函数f(x),g(x)满足:

泰勒展开式
如果两个连续的曲线想要相同,那么它们在某一点的一阶导数要相同,二阶导数也要相同,…,n阶导数也要相同,这是泰勒展开的核心思想。(曲线的变化率的变化率的变化率…都相同)

如何理解x变成了x−a了呢?从0点改到a点,相当于函数图像向右平移a个单位,即变成了x−a (左右平移是X加或减)
得到泰勒展开式为:
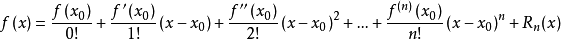
如果想要等式左右两边相等,光到n nn项是不够的,后面还有n+2,...无穷多项,n后的无穷多项通过Rn(x)来表示。
不定积分
原函数:在区间I上函数F(x)可导,F′(x)=f(x)或dF(x)=f(x)dx,那么F(x)就是f(x)在这个区间上的一个原函数。
连续函数一定有原函数
在区间I上函数f(x)的全体原函数F(x)+C称为f(x)的不定积分,记为∫f(x)dx=F(x)+C
不定积分是全体原函数(常数C的导数为0)
∫积分号,f(x)被积函数,f(x)dx被积表达式,x积分变量
微分运算与不定积分运算互为逆运算。
不定积分的性质:
∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx
∫ kf(x)dx=k ∫ f(x)dx (k,且不为零)
定积分
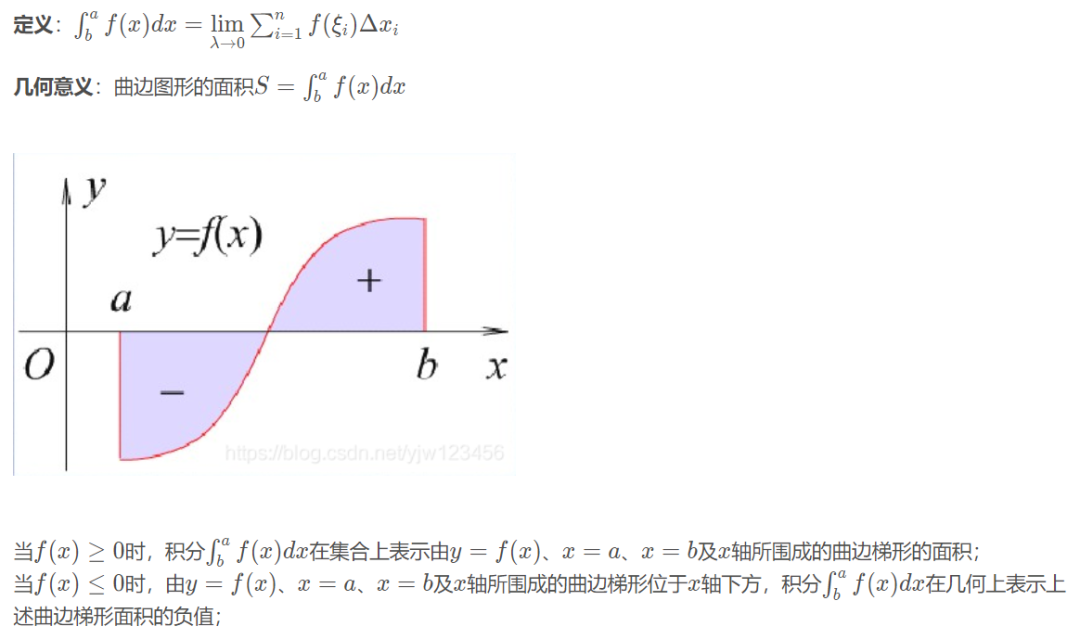
如果f(x)是[a,b]上的连续函数,并且有F′(x)=f(x),那么
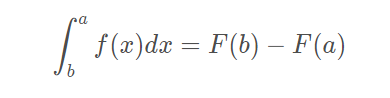
也就是说,一个定积分式的值,就是原函数在上限的值与原函数在下限的值的差。
函数单调性与极值
函数单调性

函数极值

极大值和极小值统称为极值;极大值点和极小值点统称为极值点。
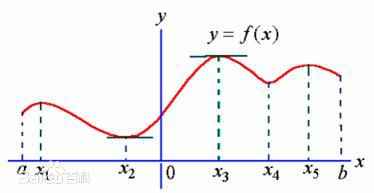
要注意是:
-
极值是局部性概念
-
可以有多个极大值或极小值
-
端点不是极值点(极值只在区间内部取得)
极值点处若f′(x)=0,这样的点称为驻点,若导数不存在,则称为尖点。
我们可以注意到,极值点两侧单调性不同,也就是导数符号不同,
根据这点,我们可以得到极值判定第一充分条件👇
极值判定(极值判定第一充分条件):

我们看上图,大概x xx取-3点处的函数值是极大值,该点出的切线斜率(导数)为0,左则切线斜率大于0,右侧切线斜率小于0。
也就是说,一阶导数在单调递减,因此二阶导数小于0。得出极值判定第二充分条件:
极值判定(极值判定第二充分条件):

曲线的凹凸与拐点
凹凸
设函数f(x)在(a,b)内可导:
若曲线f(x)上任一点切线位于曲线的下方,则称曲线在(a,b)内是凹的,区间(a,b)称为凹区间;
若曲线f(x)上任一点切线位于曲线的上方,则称曲线在(a,b)内是凸的,区间(a,b)称为凸区间;
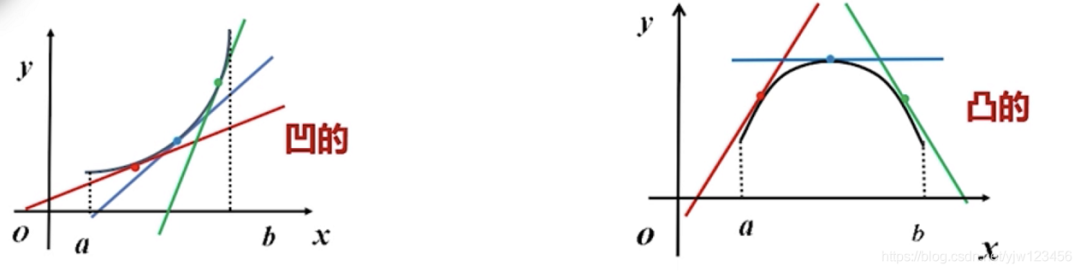
但是这是在给定了函数图像的情况下,若没有函数图像,我们该如何通过函数表达式来判断呢?
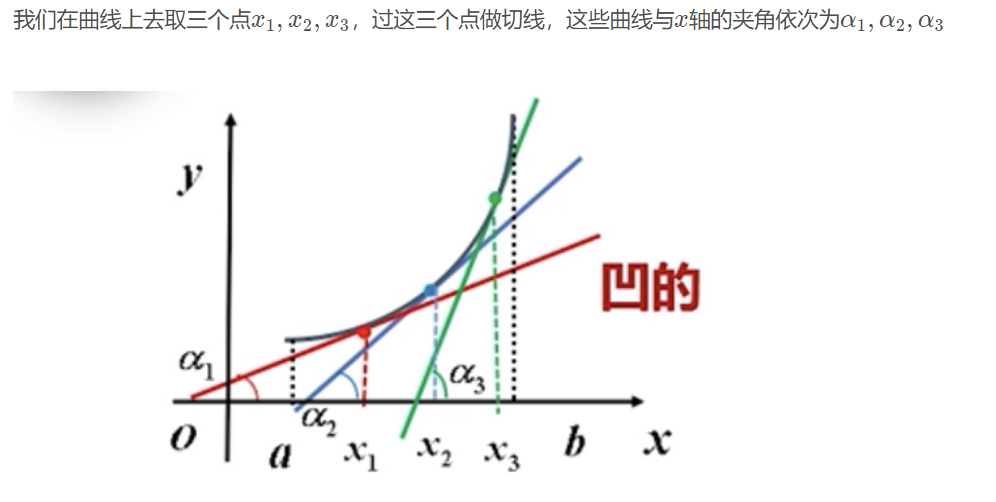
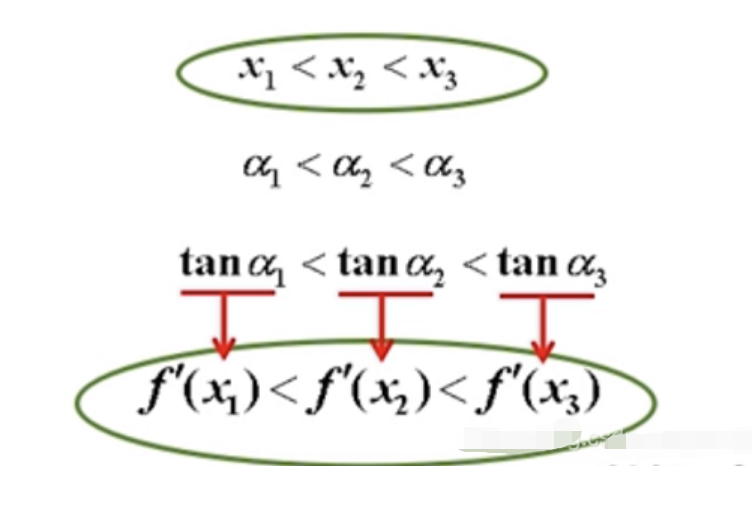
可以看到,导函数f′(x)是单调递增的,也就是f′′(x)≥0
同理,凸函数的二阶导数f′′(x)≤0
函数的凹凸性判断
如果函数f(x)在(a,b)具有二阶导数f′′(x):
-
若在(a,b)内f′′(x)>0,则f(x)在(a,b)内是凹的;
-
若在(a,b)内f′′(x)<0,则f(x)在(a,b)内是凸的;
拐点
定义:连续曲线上凹弧与凸弧的分界点称为曲线的拐点。
线代篇、概率论篇……知识盘点整理中🚀🚀🚀
关注下方《学姐带你玩AI》别错过
码字不易,欢迎大家点赞评论收藏!