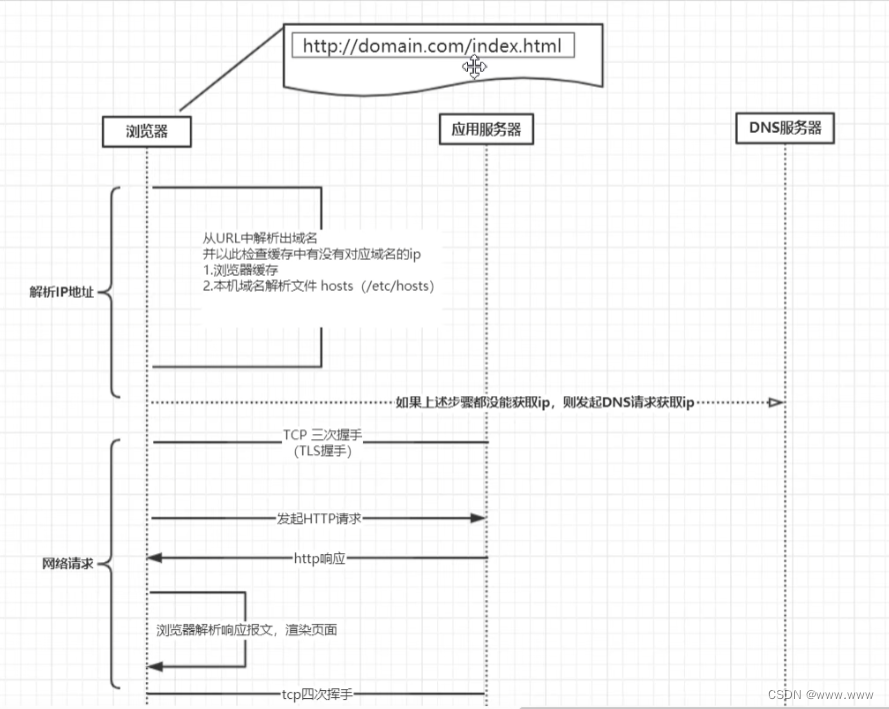
如:
k = (1:1024)';
f = @(x)(1-x-k.*x.^2);
在这段代码给出了一组函数,若需要计算f=0,可以通过自带的函数实现:
x0 = zeros(length(k),1);
options = optimoptions('fsolve','Display','none','TolX',tol,'TolFun',tol);
tic
for ik = 1:length(k)
x2(ik,1) = fsolve(@(x)(1-x-k(ik).*x.^2),x0(ik),options);
end
toc
然而这个方法比较耗时,尤其是复杂方程更加耗时:
这个时候可以采用一些迭代法进行计算:
k = (1:1024)';
f = @(x)(1-x-k.*x.^2);
df = @(x)(-1-2*k.*x);
x0 = zeros(length(k),1);
tol = 1e-8;
tic
for i = 1:100
x1 = x0 - f(x0)./df(x0);
if(all(abs(f(x1))<tol))
break;
end
x0 = x1;
end
toc结果:
两种方法的解差别不大:
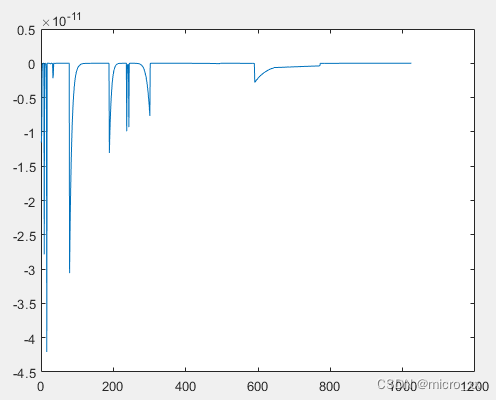
所花费的时间少很多。
![]()











![springboot2+mybatis-plus+vue3创建入门小项目[学生管理系统]02[实战篇]](https://img-blog.csdnimg.cn/img_convert/4f0ad47bb99b4df4de9b78222aa1a5c5.png)